Interakcia vrstevnatého prostredia a plošného základu

OKRAJOVÉ PODMIENKY A STRUČNÝ POPIS VÝPOČTOVÝCH MODELOV
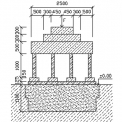
V posudzovanom experimente bola vystužená betónová platňa 2.750 × 2.750 × 125 mm zaťažovaná silou F (F = 0 až 3 MN (krok 500 kN).  odel skutočnej konštrukcie a jej základ boli v mierke 1 : 4. Podložie je reprezentované vlhkou vrstvou piesku o hrúbke 1,1 m  a ílovitým pieskom .

Sadnutia boli merané vo všetkých šiestich krokoch priťažovania, t.j. F = 0,5 ; 1,0 ; ... 3,0 MN a skutočné kontaktné napätie  bolo merané v desiatich bodoch s desiatimi napäťovými snímačmi situovanými v piesku 20 mm pod rozhraním dosky a piesku. Prehľadný model experimentu je znázornený na obr. 1.

Tento experiment bol modelovaný ako 2D úloha a pre dosiahnutie čo najväčšej zhody boli uvažované rôzne materiálové modely podložia a rôzna tuhosť základovej konštrukcie. Vstupné hodnoty popisujúce vlastnosti podložia boli nemenné, takže výsledky priebehov kontaktného napätia boli ovplyvňované hlavne vlastnosťami základovej dosky a zvoleným materiálovým modelom podložia.

Všetky výpočtové modely boli najskôr odladené na pružnom modele podložia a neskôr ako pružno plastický model. Uvažované vlastnosti zemín sú uvedené v tab. 1 a rozmery základovej dosky sú uvedené na obr. 1 pričom bola zjednodušene uvažovaná v niektorých modeloch zvýšená tuhosť dosky vplyvom blízkej vzdialenosti roznášecích pätiek. Ostatné potrebné charakteristiky, ktoré neboli uvedené v experimente  som prevzal z noriem STN.

GEO4.
Výpočtový program Geo4 – MKP má zastúpené základné materiálové modely zemín a tiež ponúka použitie preddefinovaného prvku nosníka na podloží čo je výhodou, avšak nevýhodou je, že ponúka pri vytvorení výpočtovej siete iba dva trojuholníkové prvky. A to 3-uzlový a 6-uzlový rovinný prvok, takže je možné modelovať len 2D úlohy a presnosť výpočtu je možné ovplyvniť hlavne počtom prvkov.

Celková možnosť modelovania geotechnických úloh je však prehľadná a tiež je dobre zvládnutý výstup výsledkov, kde nie je problém získať požadované grafické, prípadne číselné výstupy. Pri modelovaní podložia bol použitý lineárny model podložia (LM), Drucker – Prager (DP), Mohr – Coulomb (MC) a Mohr – Coulomb modifikovaný (MCM).

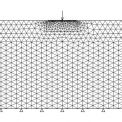
Na obr. 2 je zobrazená výpočtová schéma pre všetky modely uskutočnené v programe Geo4. Výpočtová sieť bola vytvorená z 1 143 6-uzlových trojuholníkových prvkov. Počet uzlov bol 2 514. Dĺžka strany prvkov bola 0,5 m. Sieť bola zahustená v oblasti uloženia nosníka a strana prvku v tejto oblasti bola 0,1 m. Pre zjednodušene modelovania experimentu boli vybrané tri zaťažovacie stavy (1. ZS → F = 500 kPa, 3. ZS → F = 1.500 kPa, 6. ZS → F = 3.000 kPa ) a spolu bolo vytvorených 48 výpočtových modelov. Pre každý model bol vznesený graficky priebeh kontaktných napätí, ktorý bol porovnaný s nameraným kontaktným napätím a taktiež boli výsledky spracované aj tabuľkovo a bol spracovaný tiež koeficient determinácie R₂, ktorý porovnáva odhadované (vypočítané) a skutočné hodnoty kontaktného napätia vk a nadobúda hodnoty v rozsahu od 0 do 1. Ak sa R₂ = 1, vo vzorke je dokonalá korelácia medzi odhadovanými a skutočnými hodnotami .

Pri takomto spôsobe vyhodnotenia vypočítaných údajov sa koeficient determinácie pre rôzne výpočtové modely pohyboval v rozmedzí 59,70 až 86,49 %. Zo vzájomného porovnania vypočítaných a nameranej hodnoty kontaktného napätia vyplýva, že najviac sa skutočnému priebehu kontaktného napätia približuje modelovanie pri treťom zaťažovacom stave 3. ZS čo môže byť zapríčinené hlavne tým, že prevzaté vstupné charakteristiky podložia nevystihujú spoľahlivo takú širokú škálu napätia od priťaženia akou je interval 0–400 kPa a pričom pri modelovaní bola vo výpočte menená iba tuhosť hornej stavby a materiálový model podložia (E, DP, MC, MCM).

Najlepšia zhoda bola dosiahnutá na výpočtovom modeli 4 . mc200, ktorého koeficient determinácie je až 82,40 %. Grafický výstup priebehu šestnástich vypočítaných a nameraného kontaktného napätia pre tento tretí zaťažovací stav 3. ZS je zobrazený na obr. 3. Z obr. 3 je tiež možné vyčítať miesto kde je vplyv zmeny tuhosti hornej stavby minimálny (charakteristický bod) a je to približne 0,28 . b čo je trochu menej ako udáva norma STN 731 001. Táto odchýlka môže byť spôsobená tým, že normová vzdialenosť charakteristického bodu 0,37 . b je teoretická hodnota odvodená pre dokonale tuhý a pružný základ.

Zo vzájomného porovnania materiálových modelov podložia môžeme tiež usúdiť, že najväčší vplyv má zmena tuhosti hornej stavby na pružný materiálový model podložia. Z grafických výstupov sa potvrdila fyzikálna správnosť modelov a pri tuhšej základovej doske (model 3 . mc200) boli kontaktné napätia redistribuované viacej pri okraji ako v strede pod základom oproti pružnejšiemu základu (model 4 . mc200). Vstupné parametre modelu 4 . mc200 boli ďalej použité pri modelovaní v programoch Plaxis 7.2 a Ansys 10.

PLAXIS
Program Plaxis 7.2 umožňuje použiť ako základný prvok trojuholníkový 6-uzlový element, prípadne 15-uzlový trojuholníkový prvok pre presnejší výpočet. Plaxis ponúka lineárne pružný, Mohr – Coulombov, elastoplastický model so spevnením a tiež Cam Clay materiálový model podložia. Výhodný je hlavne elastoplastický model so spevnením, ktorý je výhodnejší ako Mohr – Coulombov model. Tuhosť zeminy je tu opísaná presnejšie ako pri MC modeli a to použitím troch rozdielnych modulov pretvárnosti. V kontraste ku MC modelu, model so spevnením tiež počíta so závislosťou napätia a modulu pretvárnosti, takže všetky tuhosti narastajú s napätím.1

Ako východzí model pre zaťažovací stav 3. ZS bol považovaný model 4 . mc200 z programu Geo4 a podobne ako pri programe Geo4 aj tu bol uvažovaný najskôr pružný model podložia, potom Mohr – Coulombov a nakoniec elastoplastický model so spevnením.

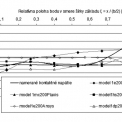
Výpočtový model bol vytvorený z 1 488 6-uzlových trojuholníkových prvkov a výsledky z týchto modelov pre 3. ZS pri rôznych materiálových modeloch podložia sú uvedené na obr. 4. Z grafického zobrazenia vyplýva, že najviac sa ku skutočnému priebehu kontaktných napätí približuje Mohr – Coulombov model podložia a stupeň korelácie dosahuje hodnotu R₂ = 86,49 %.

ANSYS
Výpočtový program Ansys 10 ponúka množstvo trojuholníkových, štvoruholníkových a rôznych iných prvkov a taktiež 3D prvky. To isté platí pre voľbu materiálového modelu podložia. Jedinou nevýhodou tohto programu je, že to nie je geotechnický program a preto nemá databázu zemín a tiež programové rozhranie nie je prispôsobené geotechnickým úlohám tak ako je to pri výpočtovom programe Geo4 či Plaxis 7.2. Avšak univerzálnosť a najlepšie možnosti modelovania ľubovoľnej úlohy sú veľkou výhodou tohoto programu.

Úloha bola v programe Ansys 10 modelovaná v zmysle predpokladov teórie lineárne pružného polpriestoru ako rovinná úloha. Úloha bola modelovaná ako 2D tiež z dôvodu objektívnosti porovnania použitých výpočtových programov. Delenie modelu na konečné prvky bolo volené tak, aby boli podrobnejšie rozdelené oblasti predpokladaných koncentrácií napätí (rohy, resp. okraje základu a kontakt základu s podložím). Pre analýzu spolupôsobenia plošného základu s podložím v závislosti od možného prenosu silových účinkov medzi základom a podložím bol definovaný model s dvojstrannou väzbou. Pri delení modelu podložia a základu bol použitý rovinný homogénny 8-uzlový prvok PLANE82. Uvažované boli dva modely podložia a to lineárny elastický a Drucker – Pragerov model podložia. Všeobecne známou nevýhodou zvoleného spojitého výpočtového modelu je prenos ťahových síl medzi základovou konštrukciou a podložím, avšak pri uvažovanom spôsobe a veľkosti zaťaženia nedošlo k odlepovaniu základu a mohla byť využitá výhoda spojitého výpočtového modelu čo je numerická stabilita a jednoduchosť výpočtu.

Pri výpočte boli použité už spomínané vstupné charakteristiky z programu Geo4. Grafické výsledky výpočtov pomocou programu Ansys 10 sú úvedené spolu s grafickými výstupmi z programu Plaxis 7.2 na obr. 4.

Z grafického zobrazenia vyplýva, že najviac sa ku skutočnému priebehu kontaktných napätí približuje Drucker – Pragerov model podložia a stupeň korelácie dosahuje hodnotu R₂ = 83,12 %.

VÝSLEDKY A ICH ZHODNOTENIE
Porovnanie vypočítaných a nameraných hodnôt kontaktného napätia pre tretí zaťažovací stav 3. ZS je uvedené na obr. 3 a obr. 4. V programe Geo4 sa najviac k skutočným hodnotám priblížil model 4mcm200 a jeho koeficient determinácie bol 82,40 %. V programe Plaxis 7.2 bol najvýstižnejší model 2mc200 Plaxis a jeho koeficient determinácie bol 86,49 % a v programe Ansys 10 bol najvýstižnejší model 2dp200 Ansys a jeho koeficient determinácie bol 83,12 %.

Z výsledkov vyplynulo, že vo všetkých použitých programoch bol najvýstižnejší elasto – plastický model podložia (MC a DP) a to pri treťom zaťažovacom stave 3. ZS, kde sa vypočítané hodnoty kontaktného napätia najviac približovali k nameraným hodnotám. Čo znamená, že prevzaté vstupné charakteristiky podložia vystihujú najlepšie správanie podložia práve pri tomto zaťažení.

ZÁVER
Všeobecne je známe, že interakciu medzi podložím a základom ovplyvňuje množstvo faktorov. Je preto zrejmé, že k dosiahnutiu optimálnej zhody vypočítaných a nameraných údajov je potrebné množstvo vstupných údajov, ktoré umožnia vytvorenie čo najreprezentatívnejších výpočtových modelov a tie nám potom poskytnú spoľahlivé prognózy. V tomto prípade som mal dostupné obmedzené informácie o veľkorozmernom pokuse, ktorý v roku 1990 uskutočnil Czezarskij a Murzenko. No aj napriek tomu sa mi podarilo dosiahnuť hlavne pri treťom zaťažovacom stave prijateľné výsledky, ktoré korešpondujú s nameranými hodnotami a to pri všetkých použitých programoch.

Tento príspevok vznikol v rámci riešenia grantovej úlohy MŠ SR č. 1/0578/08.

ZDROJE INFORMÁCIÍ:

• Jesenák J.: Mechanika zemín, STU Stavebná fakulta, • kulta, Bratislava 1994
• Hruštinec Ľ.: Analýza spolupôsobenia plošného základu s podložím, 1. vyd. Bratislava, Vydavateľstvo STU, 2003, 184 s.
• Kolář V. – Němec I.: Contact stress and settlement in the structure soil interface, 1st ed. Praha, ACADEMIA 1991, 160 s.
• Feda, J.: Napjatost podzákladí a metódy výpočtu konečného sednutí, 1. vyd. Praha, ACADEMIA 1974, 152 s.
• Norma STN 731001 Základová pôda pod plošnými základmi, Praha 1987
• Manual – Plaxis finite element code for soil and rock analyses, version 7, Reference and Material models manual, Netherland, 1998
• Plaxis finite elem. code for soil and rock analys., version 7, Material models manual, Netherland, 1998, p. 1–1

Analysis of interaction between layered subsoil and spread foundation
Because at interaction between non-homogeneous subsoil and building construction is experimental measuring very expensive. It is not possible to investigate individually each factor affecting the interaction. For all that is needed to recognize extremes of construction behaviour under various conditions by parametric study. In this task is solving parametric study, which point on an optimal analysis model and some problems with soil structure interaction modelling. In analysis models are considered different factors.

Autor

• Ing. Černý Miroslav