Výpočetní modely styčníků ocelových konstrukcí

• Foto

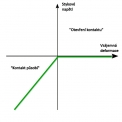
V neprutových částech ocelové konstrukce je situace složitější. Průběh napětí v průřezech není pravidelný, viz obr. 1. Jeho studium a pochopení vyžaduje složitější matematické modely. Většina jevů je výrazně nelineární povahy, např. plastizování materiálu plechů, kontakty mezi čelními deskami nebo mezi patními deskami a betonovým základem, jednostranné působení šroubů a kotev, svary, viz (Jaspart a Demonceau 2008). Normy, ČSN EN1993-1-8 i odborná literatura např. nabízí inženýrské metody řešení. Jejich obecným rysem je, že jsou odvozeny pro typické tvary konstrukcí a jednoduchá namáhání, viz (Kuhlmann a Kühnemund 2001). Jejich použití je obvykle pracné, metody se obtížně algoritmizují a zpravidla málo vypovídají o skutečném chování.

LZE PŘÍPOJE NAVRHOVAT JINAK?
Lze a dále jsou předloženy výsledky první fáze výzkumného a vývojového projektu na pokročilé navrhování styčníků ocelových konstrukcí. Po několikaleté teoretické přípravě máme příležitost pracovat na projektu „Pokročilý software pro optimální návrh obecných styčníků stavebních ocelových konstrukcí“ podpořený Technologickou agenturou ČR. Řešitelský tým byl sestaven z pracovníků firmy IDEA RS s. r. o., Katedry ocelových a dřevěných konstrukcí stavební fakulty ČVUT v Praze a Ústavu kovových a dřevěných konstrukcí stavební fakulty VUT Brno. Projekt začal letos a bude dokončen v roce 2015. Vývojový tým si dal za cíl vymyslet, vyvinout a ověřit metodu:

• Dostatečně obecnou, aby byla použitelná pro naprostou většinu styčníků, kotvení a detailů ze stavební praxe.
• Dostatečně jednoduchou a rychlou, aby pro běžnou praxi statika poskytovala výsledky ve srovnatelném čase jako doposud existující metody a nástroje.
• Dostatečně srozumitelnou, aby inženýr – statik získal jasnou informaci o chování styčníku, o namáhání a rezervách jednotlivých jeho částí a celkové bezpečnosti a spolehlivosti návrhu.

POČÍTEJME METODOU KONEČNÝCH PRVKŮ A NELINEÁRNĚ
Pro výpočet detailů ocelových konstrukcí lze využít principů metody konečných prvků (např. O. C. Zienkiewicz and Taylor R). Geometrický model přípoje je rozdělen do základních komponent typu deska, šroub, betonová patka, které jsou propojeny do jednoho výpočtového modelu. Výsledkem výpočtu jsou základní veličiny, jako jsou napětí a poměrná přetvoření v deskových částech, síly přenášené šrouby nebo síly přenášené vazbami představující svar. Veličiny jsou dále využity pro posouzení jednotlivých komponent a přípoje jako celku z hlediska únosnosti a tuhosti. Obecně platí, že většina komponent v přípojích vykazuje nelineární vlastnosti. Úloha se proto řeší nelineárně za předpokladu malých deformací.

Materiálový model prutů a plechů
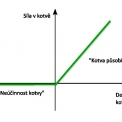
Ocelové přípoje jsou tvořeny připojovanými profily doplněnými výztužnými prvky, které lze geometricky rozložit do jednotlivých desek. Pro tyto desky je použito plošného prvku přenášejícího jak membránové, tak i ohybové složky. Protože se hledá skutečná únosnost přípoje, je v materiálovém modelu zohledněno plastické chování oceli. Použití napětí získaných lineárním výpočtem by vedlo ke konzervativnímu odhadu a zkreslilo skutečné chování. Ve stavební praxi se skutečný pracovní diagram pro návrh nahrazuje ideálně plastickým materiálem, viz obr. 2. Výhodou ideálně plastického materiálu je, že stačí znát pouze mez kluzu a modul pružnosti pro popis materiálové křivky. Stavební oceli mají zaručenou tažnost 15 %. Za předpokladu lineární míry přetvoření a vzhledem k použitému plastickému modelu lze použít reálnou mezní hodnotu plastického přetvoření přibližně 5 %.

Model šroubového spoje a kotevního šroubového spoje
Model šroubového spoje je popsán jako nelineární kontakt mezi dvěma plechy s odpovídající tahovou a smykovou tuhostí, viz (Razavi a kol 2007). Kotevní šroubový spoj je modelován jako nelineární kontakt mezi betonovým blokem a patním plechem. Podloží (betonová patka) je účinné pouze v tlaku, tak jak to ukazuje následující graf pracovního digramu podloží viz obrázek 3. Výsledné kontaktní tlaky jsou použity pro posouzení, zda nedojde k drcení betonu.

Kotevní šroub je modelován jako pružina, která pracuje v tahu a je neúčinná v tlaku. Pracovní diagram šroubu je na obrázku 4. Výsledná síla je použita pro následné posouzení únosnosti kotevního šroubu.

VÝPOČETNÍ MODEL MKP SE VYTVOŘÍ AUTOMATICKY
Projektant se sestavením MKP modelu nemusí zabývat. Jak lze automaticky připravit model MKP a posudek styčníku, lze ukázat na příkladu svařovaného styčníku horního pasu vazníku viz obrázek 5.

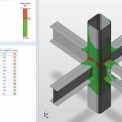
Horní pás z profilu HEA280 je namáhán tlakovou silou 1 336 kN, posouvající síla je 147 kN a ohybový moment 70 kNm. Ve svislici z K120/120/10 je tlak 683 kN a v diagonále z K110/110/8.8 je tah 611 kN. Obrázek 6 ukazuje poměrné přetvoření stěny pasu. Maximální hodnota je 28 %, tedy mezní hodnota 5 % je několikanásobně překročena – viz oblasti vyznačené červeně. Přípoj není možné takto realizovat.

I profil horního pasu musí být vyztužen výztuhami. Obrázek 7 ukazuje vliv dvou svislých výztuh navazujících na pásnice svislice a diagonály.

Zde je patrné výrazné zlepšení, maximální hodnota poměrného protažení poklesla na 3,8 %, ale styčník už vyhovuje. Projektant ovšem může řešení styčníku dále optimalizovat. Zajímavým řešením jsou i dvě šikmé výztuhy nad svislicí a diagonálou viz obrázek 8.

Řešení se ukazuje jako nejlepší. Stěna I-profilu sice stále plastizuje, ale v mnohem menší oblasti. Maximální hodnota poměrného protažení je pod 1 %. Příklad ukazuje, jak lze vhodným uspořádáním výztuh výrazně ovlivnit únosnost styčníku.

Ani kotvení není problém
Další možnosti metody analýzy styčníků lze ukázat na příkladu kotvení sloupu. Konec sloupu a patní deska jsou modelovány konečnými prvky, kotvy jsou nelineární pružiny a betonová patka se chová jako podloží.

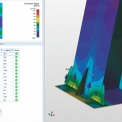
Obrázek 9 nás jasně informuje, ve kterých místech bylo dosaženo meze kluzu materiálu. V kotvách jsou spočítány skutečné síly. Celý výpočet patky trval 3 sekundy. Jednotlivé prvky lze studovat samostatně. Na obrázku 10 jsou ukázány detailní výsledky na patní desce.

Obrázek 10 ukazuje přehledné výsledky pro posouzení patní desky a betonového základového bloku. V barevné části dochází k tlaku plechu na beton, ve zbylé části není mezi materiály kontakt.

Metoda umožňuje analyzovat různé typy namáhání. Lze ji bez problému použít například pro výpočet patky sloupu namáhaného ohybovými momenty v obou směrech – viz obrázek 11.

POSOUZENÍ JEDNOTLIVÝCH PRVKŮ PŘÍPOJE
Analýza metodou konečných prvků poskytne věrohodnou informaci o rozložení napětí a sil ve všech prvcích přípoje. Tím je vytvořen základní krok pro posouzení přípoje podle platné normy. Pro posouzení svarů, šroubů nebo betonu základu lze použít poměrně jednoduché vzorce podle metody komponent.

Posouzení jednotlivých plechů lze provést na maximální dosažené poměrné plastické přetvoření. Na obrázku 12 je prezentace výsledků posudku prostorového styčníku kombinovaného z uzavřených i otevřených profilů. Barevné části projektanta informují, kde materiál plastizuje. Červená barva signalizuje, kde již bylo překročeno mezní plastické přetvoření.

SHRNUTÍ – NÁVRHOVÝ NÁSTROJ PRO KAŽDODENNÍ PRAXI
Předložená metoda umožňuje optimální návrh styčníků ocelových konstrukcí. Výsledky poskytují statikovi jasnou informaci, na kolik jednotlivé části styčníku a styčník jako celek vyhoví, jakých deformací a vnitřních sil bylo při daném namáhání dosaženo, co se v něm vlastně děje. Rychlost a pracnost jsou srovnatelné se stávajícími metodami, např. metodou komponent pro otevřené průřezy a návrhovými vzorci na únosnost styčníků uzavřených průřezů. Metoda umožňuje přesně analyzovat detaily, které musel projektant-statik doposud jen odhadovat. Metoda byla implementována do programu Connection, který je součástí výpočetního a dimenzačního software IDEA StatiCa. Program je již projektantům k dispozici.

Výzkum je podpořen grantem Pokročilý software pro optimální návrh obecných styčníků stavebních ocelových konstrukcí TA03010680.

LITERATURA:

• ČSN EN1993-1-5, Navrhování ocelových konstrukcí, Boulení stěn, ČNI, Praha, 2006.
• ČSN EN1993-1-8, Navrhování ocelových konstrukcí, Navrhování styčníků, ČNI, Praha, 2006.
• Da Silva Simoes L.: Towards a c onsistent design approach for steel joints under generalized loading, Journal of Constructional Steel Research, 64, 1059–1075, 2008.
• J.-P., Demonceau J.-F.: European design recommendations for simple joints in steel structures. Journal of Constructional Steel Research, 64, 7–8, 2008, 822–832.
• Kuhlmann U., Kühnemund F.: Komponente Stützensteg auf Druck – Traglast unter Berücksichtigung einer Stützennormalkraft. Priebe, J. Eberwien, U. (Hrsg.): Festschrift zu Ehren von Prof. Dr.-Ing. Günther Valtinat, 2001, 291–300.
• Razavi H, Abolmaali A, Ghassemieh M., Invisible elastic bolt model concept for finite element analysis of bolted connections, Journal of Constructional Steel Research 63, 2007, 647–657.
• Zienkiewicz O. C., Taylor R. L., The Finite Element for Solid and Structural Mechanics, Elsevier Butterworth-Heinemann, Oxford UK, 6thedition, 2005.
• Braun B., Kuhlmann U., Reduced stress design of plates under biaxial compression. Steel Construction 5, No. 1, 2012, 33–40.

Calculation Models of Steel Structure Joints
Designing a steel structure, a structural designer most frequently uses beam elements, however there are places of a structure where the beam theory cannot be applied, e.g. welded joints, bolted connections, anchorage, wall openings, changes to section height and local burdens. For these cases, structural designer does not normally have a sufficiently general assessment tool. The article describes a brand new method of the solution of common joints and steel structure details. The solution principle is a combination of generally known component method with a calculation by means of final elements.

Autoři

• Prof. Ing. Wald František CSc.
• Prof. Ing. Bajer Miroslav CSc.
• Ing. Šabatka Lubomír CSc.
• Ing. Kabeláč Jaromír

Výpočetní modely styčníků ocelových konstrukcí