Vliv koncových přípojů ocelových prutů na jejich kritické zatížení
Rubrika: Projektování
V posledních letech přišel tým vývojářů IDEA StatiCa společně s českými universitami, ČVUT FSv v Praze, FAST VUT v Brně, s novou metodou CBFEM pro řešení styčníků ocelových konstrukcí. Metoda se rychle vžila a její přijetí technickou veřejností vyvolalo otázku, zda se podobný model nehodí i na další příklady v projekční praxi. V článku je popsán návrh využití metody pro analýzu vzpěru a klopení ocelových prvků.
ZÁKLAD CBFEM METODY
Component Based Finite Element Method (CBFEM) [1] sdružuje metodu konečných prvků a metodu komponent. Metodu komponent lze využít pro jednoduché případy, zejména přípoje nosníků tvaru I na sloup tvaru H. Pro složitější příklady se musí přistoupit k řadě inženýrských odhadů, například na polohu osy otáčení či interakci momentů kolem dvou os, normálové a posouvající síly. Metoda konečných prvků dokáže inženýrské odhady zpřesnit a dovoluje návrh i složitých styčníků namáhaných libovolnou kombinací zatížení. V CBFEM jsou komponenty, jako například šrouby, uvažovány jako nelineární pružiny s tuhostí a únosností stanovenou pomocí metody komponent [2], podrobnějších dokumentů [3] či experimentů. Plechy jsou modelovány jako deskostěnové elementy s bilineárním materiálovým diagramem a kritériem plasticity podle von Misese. V přípojích je na mezi únosnosti předpokládáno plastické působení, a tudíž jsou plechy posuzovány na 5% mezní přetvoření [4]. Svary jsou modelovány speciálním konečným prvkem s vazbami na svařené plechy. Tento konečný prvek dovoluje roznášet napětí z oblastí se singularitou (extrémem napětí kvůli nepřesnosti sítě konečných prvků) dále po délce svaru. Tím lze rychle a snadno posoudit i například svar na nevyztuženou pásnici sloupu. Metoda CBFEM je s úspěchem využita v programu IDEA StatiCa Connection, který už překonal hranici 2 000 licencí po celém světě. Tento článek přináší možné rozšíření metody CBFEM na návrh připojovaného prvku. V současnosti je k dispozici analýza s materiálovou nelinearitou (plastický výpočet) a analýza vlastních tvarů.
POSTUP STANOVENÍ ÚNOSNOSTI
Z analýzy vlastních tvarů lze získat násobek zatížení, při kterém dojde k pružné ztrátě stability konstrukce s ideální geometrií, např. kritickou sílu pro osově zatížený prvek nebo kritický moment pro příčně namáhaný nosník. Z kritického zatížení lze dopočítat štíhlost prutu a jeho únosnost [5]. Podle EN 1993-1-1 – 6.3.4 lze řešit i kombinace zatížení. Obecná metoda využívá kombinace plastického výpočtu (získáme násobek zatížení αult,k) a analýzy vlastních tvarů (násobek zatížení αcr,op). Z těchto dvou hodnot lze dopočítat štíhlost prvku či části konstrukce:
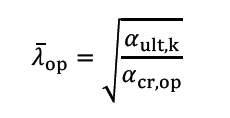
Z poměrné štíhlosti se určí součinitel χop jako minimum ze součinitele vzpěru χ, čl. 6.3.1, a součinitele klopení χLT, čl. 6.3.2. Přestože se metoda nazývá „obecná“, je omezena na některé průřezy, pro které byla její platnost ověřena.
PŘÍČNĚ ZATÍŽENÝ NOSNÍK
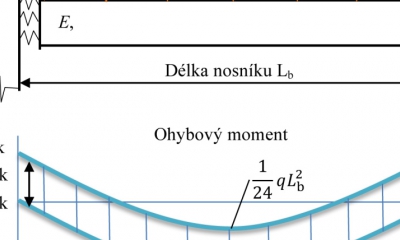
Okrajové podmínky mají velký význam pro stanovení ohybové únosnosti nosníků s vlivem klopení. Zásadní vliv mají na průběh ohybových momentů a hodnoty kritického momentu Mcr, viz obrázek 1. V národní příloze ČSN EN 1993-1-1 [5] je postup stanovení kritického momentu podle prof. Melchera odvozený z Vlasova [6]. Okrajové podmínky určují součinitel uložení kolem tuhé osy ky, uložení kolem měkké osy kz, a deplanace kw. Součinitele nabývají v případě, že není zabráněno deformaci hodnoty 1,0 a oboustranně zabráněné deformaci 0,5. Podle průběhu ohybových momentů jsou stanoveny hodnoty součinitelů C1, C2 a C3.
V následujících příkladech je nosník s průřezem IPE 300 z oceli pevnostní třídy S355 s teoretickou délkou 8 m. Zatížení je uvažováno na horní pásnici nosníku. Kritické momenty, únosnosti včetně vlivu klopení a další mezivýsledky jsou shrnuty v tabulce 1.
Tabulka 1 – Shrnutí výpočtů klopení nosníků s různými okrajovými podmínkami podle národní přílohy ČSN EN 1993-1-1
| ky | kz | kw | C1 | C2 | C3 | Kwt | ζg | ζj | μcr | Mcr | λ´LT.pl | ΦLT,pl | χLT,pl | Mb,pl,Rd |
| [–] | [–] | [–] | [–] | [–] | [–] | [–] | [–] | [–] | [–] | [kNm] | [–] | [–] | [–] | [kNm] |
| 1 | 1 | 1 | 1,13 | 0,46 | 0,53 | 0,501 | 0,520 | 0 | 1,022 | 57,68 | 1,966 | 2,618 | 0,230 | 51,28 |
| 1 | 1 | 0,5 | 1,23 | 0,39 | 0,81 | 1,001 | 0,520 | 0 | 1,509 | 85,15 | 1,618 | 1,958 | 0,327 | 72,85 |
| 0,5 | 1 | 1 | 2,595 | 1,56 | -0,86 | 0,501 | 0,520 | 0 | 1,480 | 83,53 | 1,634 | 1,985 | 0,321 | 71,63 |
| 0,5 | 0,5 | 0,5 | 1,75 | 0,83 | 0,00 | 1,001 | 1,040 | 0 | 2,781 | 156,92 | 1,192 | 1,315 | 0,535 | 119,29 |
Pro nosník v patrové budově, který je zatížen spojitým zatížením 15 kN/m. Při stanovení vnitřních sil na nosníku se uvažuje s vlivem tuhosti okolních prutů. Sloupy jsou z průřezu tvaru HEA 400 s teoretickou délkou 3 m. U kloubově uložených nosníků je pozice kloubu uvažována na líci sloupu, viz obrázek 2.
STUDIE OHYBOVĚ-TUHÉHO PŘIPOJENÍ
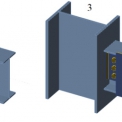
V připravovaném software IDEA StatiCa byl studován vliv ohybové tuhosti rámových přípojů na stabilitu prutu. Přípoj čelní deskou bez výztuh je podle tloušťky čelní desky na hranici tuhých a polotuhých přípojů. Výsledky jsou shrnuty v tabulce 2. Ukazuje se, že výztuhy ve sloupu, přestože HEA 400 je masivní průřez, jsou pro zabezpečení dostatečné tuhosti a zabránění deplanace nosníku nutné.
Tabulka 2 – Srovnání kritického momentu pro různé typy rámových přípojů
| Typ přípoje |
αcr |
Mcr |
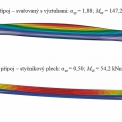
| 1 Svařovaný přípoj + výztuhy sloupu | 1,88 | 147,2 |
| 2 Příložky + výztuhy | 1,85 | 144,9 |
| 3 Čelní deska + výztuhy + náběh | 1,78 | 139,4 |
| 4 Čelní deska + výztuhy + náběh2 | 1,78 | 139,4 |
| 5 Čelní deska + výztuhy | 1,77 | 138,6 |
| 6 Čelní deska | 1,47 | 115,1 |
| 7 Svařovaný přípoj | 1,43 | 112,0 |
STUDIE KLOUBOVÉHO PŘIPOJENÍ
U kloubových přípojů byl zkoumán vliv zabránění deplanace vytvořením uzavřeného průřezu na konci nosníku. Krátké výztuhy nedokáží účinně zabránit deplanaci. S rostoucí délkou se jejich účinnost zvyšuje.
Tabulka 3 – Srovnání kritického momentu pro různé typy kloubových přípojů
| Typ přípoje | αcr [–] |
Mcr [kNm] |
| 1 Krátká čelní deska | 0,47 | 50,9 |
| 2 Styčníkový plech (t = 10 mm) | 0,50 | 54,2 |
| 3 Styčníkový plech + výztuha (dl. 200 mm) | 0,61 | 66,1 |
| 4 Styčníkový plech + výztuha (dl. 300 mm) | 0,68 | 73,6 |
POROVNÁNÍ
Kritický moment je pro poměrně tuhé vetknutí i kloub nižší než podle normového výpočtu dle Vlasovovy teorie, viz tabulku 4. To je způsobeno zejména kvůli rozdílnému momentu tuhosti v kroucení. Moment tuhosti v kroucení It se pro průřezy tvaru I stanovuje jako:
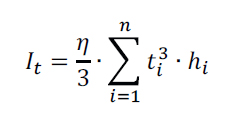
kde součinitel η je určen z experimentů, zohledňuje vliv zaoblení a uvažuje se přibližně 1,2. Deskostěnové prvky nedokáží vliv zaoblení zahrnout. Moment tuhosti v kroucení je pro IPE 300 podle tabulkových hodnot It = 201 000 mm4 a bez vlivu zaoblení (η = 1) It = 157 000 mm4.
Kritický moment pro stanovení ohybové únosnosti příčně zatíženého nosníku náchylného ke klopení vychází v připravovaném software IDEA StatiCa přibližně na stranu bezpečnou o 10 % menší.
Tabulka 4 – Srovnání deskostěnových modelů s teoretickým řešením
| Typ přípoje |
IDEA StatiCa |
ČSN EN 1993-1-1 |
LTBeam [7] |
||
| It = 20 cm4 | It = 16 cm4 | It = 20 cm4 | It = 16 cm4 | ||
|
Tuhý přípoj |
147,2 | 156,9 | 143,6 | 153,9 | 141,9 |
|
Kloubový přípoj |
50,9 | 57,7 | 51,3 | 57,4 | 51,3 |
|
Kloub + zabránění deplanace |
73,6 | 85,2 | 71,6 | 84,2 | 79,2 |
STUDIE OSOVĚ ZATÍŽENÉHO NESYMETRICKY PŘIPOJENÉHO PRUTU
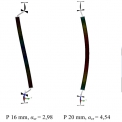
Předloženou metodou lze řešit i chování prutů při vzpěru. Častým zdrojem poruch je připojení tlačených prvků pomocí nesymetricky umístěných připojovacích plechů. Z obrázku 6 je vidět vliv tloušťky plechů na tvar vybočení. Pro štíhlé plechy zůstává prut prakticky nedeformovaný. Vybočují připojovací plechy. Teprve při větší tloušťce plechů se prut chová jako prut s očekávaným sinusovým tvarem vybočen.
ZÁVĚR
Výpočet pomocí kritického zatížení či za pomoci obecné metody může vést k dobrému odhadu únosnosti prutů náchylných ke stabilitním problémům. Návrh standardních prutů je podrobně prozkoumán, avšak okrajové podmínky jsou většinou pouze předpokládány. Z výše uvedené studie je zřejmé, že konstrukční řešení styčníku má nezanedbatelný vliv na kritický násobek zatížení. Tento vliv lze ověřit pouze na detailním skořepinovém modelu prutu včetně styčníku.
Metodu CBFEM využívá software IDEA StatiCa Connection, který se stává světovým standardem pro navrhování styčníků ocelových konstrukcí s více než 2000 licencemi. IDEA StatiCa připravuje pro své uživatele nový produkt pro návrh komplikovaných prvků včetně jejich styčníků. Cílem je poskytnout široké škále uživatelů optimalizované konečně-prvkové modely nosníků a sloupů v jednoduchém uživatelském rozhraní.
Článek byl vytvořen v rámci řešení projektu č. TH02020301 – Pokročilý návrh zesilování ocelové konstrukce pod zatížením. Materiál byl prezentován na konferenci KONSTRUKCE 2018.
REFERENCE:
[1] Wald, F.; Šabatka, L.; Bajer, M.; Barnat, J.; Gödrich, L.; Holomek, J.; Jehlička, P.; Kabeláč, J. et al., Benchmark cases for advanced design of structural steel connections, Praha: Česká technika – nakladatelství ČVUT, 2016.
[2] ČSN EN 1993-1-8 Eurokód 3: Navrhování ocelových konstrukcí – Část 1-8: Navrhování styčníků. Praha: ÚNMZ, 2013.
[3] VDI2230 Systematic calculation of high duty bolted joints – Joints with one cylindrical bolt. Association of German Engineers: Berlin, 2003.
[4] ČSN EN 1993-1-5 Eurokód 3: Navrhování ocelových konstrukcí – Část 1-5: Boulení stěn. Praha: ČNI, 2008.
[5] ČSN EN 1993-1-1 Eurokód 3: Navrhování ocelových konstrukcí – Část 1-1: Obecná pravidla a pravidla pro pozemní stavby. Ed. 2. Praha: ÚNMZ, 2011.
[6] Vlasov, V.Z. Tenkostěnné pružné pruty. Praha: SNTL, 1962, 571 stran.
[7] CTICM. Software LTBeam v. 1.0.11. Dostupné z: https://www.cesdb.com/ltbeam.html