Svařování a dělení
Svařování a dělení  Pravděpodobnostní přístup k posudku únavové životnosti svarového spoje
Pravděpodobnostní přístup k posudku únavové životnosti svarového spojePravděpodobnostní přístup k posudku únavové životnosti svarového spoje
Rubrika: Svařování a dělení
Norma ČSN EN 1993-1-9 (2006) [1] uvádí metody posuzování pro prokazování únosnosti při únavě pomocí křivek únavové pevnosti, které platí pro (a) běžné detaily při působení jmenovitých napětí (b) doporučená uspořádání svarů při působení extrapolovaných jmenovitých napětí. V doporučení IIW, viz Hobbacher [2], je navíc uveden postup (c) vycházející z efektivního vrubového napětí na hranici fiktivního vrubu, umístěného v místě iniciace trhliny. Všechny tři uvedené metody hodnocení únavové odolnosti vycházejí z analýzy napětí za předpokladu lineárně elastického chování materiálu.
Široce používaný v normách zavedený postup únavového posouzení (a) vychází ze jmenovitých napětí (eventuálně modifikovaných jmenovitých napětí) v základním materiálu (případně svaru), vypočítaných podle obecně přijatých vzorců pružnosti a pevnosti v průřezu předpokládaného vzniku únavové trhliny. Odpovídá výpočetním možnostem a době před širším uplatněním metody konečných prvků. Závislost rozkmitů normálových napětí Δσ na počtu cyklů zatížení N pro různé kategorie detailů KD 36 až KD 160 je vynesena v síti S-N křivek, křivek únavové pevnosti, viz [1].
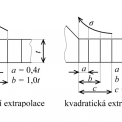
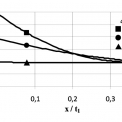
Koncepci (b) extrapolovaného jmenovitého napětí (hot spot stress) je možno použít pro svařované detaily, u kterých začíná únavové poškození z úpatí svaru. Extrapolované jmenovité napětí se stanoví výpočtem metodou konečných prvků, nebo tenzometrickým měřením. Extrapolované jmenovité napětí σhs v úpatí svaru se počítá z napětí vypočítaných (nebo naměřených) v referenčních bodech. Představu o jeho stanovení lze získat z obr. 1, kde jsou uvedena doporučení pro vzdálenosti a, b, c, referenčních bodů od úpatí svaru podle [2, 3] pro lineární a pro kvadratickou extrapolaci napětí σ.
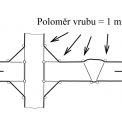
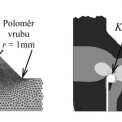
Běžnou koncepci vrubového napětí používanou ve strojírenství není možno pro svarové spoje přímo použít. Nepravidelnost úpatí svaru a konfigurace kořene svaru brání běžnému stanovení vrubového napětí. Jak uvádí Hobbacher [2, 3], nejnovější výzkumy ukázaly, že nepravidelný vrub na svarových spojích je možné nahradit efektivním vrubem o poloměru 1 mm, viz obr. 2. Efektivní vrubové napětí pro postup (c) je definováno jako maximální ekvivalentní napětí (von-Mises stress) na hranici fiktivního vrubu, umístěného v místě iniciace trhliny. Je možno je stanovit metodou konečných prvků (nebo metodou hraničních prvků). Metoda umožňuje posoudit jak úpatí svaru, tak i případ iniciace trhliny z kořene svaru.
Odolnost proti únavě ve vztahu k výše uvedeným napětím udávají různé na základě experimentů získané S-N křivky pro konstantní rozkmity normálových (obdobně smykových) napětí
NΔσm = C (1)
kde N je počet cyklů do lomu, Δσ rozkmit normálových napětí, exponent m (sklon křivky v souřadnicích log N - log Δσ) a materiálová konstanta C se získají z výsledků zkoušek lineární regresí.
Účinky únavového zatížení na křížovém spoji s koutovými svary
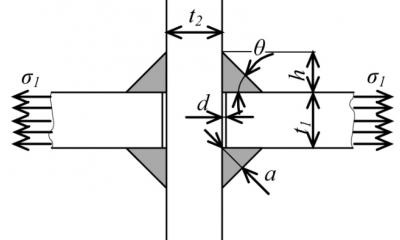
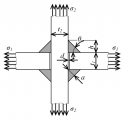
Předmětem pravděpodobnostního posouzení únavové odolnosti je křížový svarový spoj podle obr. 3. Nominální napětí σ1 (koutové svary přenášejí zatížení) je v přerušené desce o tloušťce t1.
Z obr. 4 je zřejmá závislost vypočítaného extrapolovaného jmenovitého napětí σhs na poloze referenčních bodů (vzdáleností a, b, c). Pro x = 0 je σ/σnom = khs, a proto σhs = khs × σnom.
V levé části obr. 5 je nakreslená síť konečných prvků v blízkosti svaru použitá pro výpočet efektivního vrubového napětí. Efektivní vruby o poloměru r = 1 mm byly modelovány v kořeni svaru a v úpatí svaru. Výsledky napěťové analýzy jsou znázorněny v pravé části obr. 5. Pro efektivní vrubové napětí σnotch v kořeni svaru vyšlo Kt = σnotch/σnom = 5,4664, kde σnom = σ1, σ2 = 0, viz obr. 3. Obdobně pro efektivní vrubové napětí v úpatí svaru vyjde Kt = σnotch/σnom = 4,1204, jak je také vyznačeno v pravé části obr. 5.
Pravděpodobnostní posouzení doby života svarového spoje
Spektrum rozkmitů jmenovitých normálových napětí Δσi (v obr. 3 to jsou napětí σ1, dále je počítáno s tím, že napětí σ2 = 0) s četnostmi ni jejich výskytu pro jeden zatěžovací blok je v tabulce 1. Rozkmity napětí Δσi v jednotlivých stupních jsou uvažovány jako náhodné veličiny s rovnoměrným rozložením (uniform distribution), viz Marek P. et al. [4, 5]. Počty cyklů jsou považovány za náhodné veličiny s omezeným normálním rozdělením (normal distribution), opět viz [4, 5]. Trilineární S-N křivka životnosti je uvažována s konstantními exponenty m = 3 a m = 5, rovnice (1), viz [1, 2]. Změna sklonu křivky nastává při rozkmitu napětí ΔσD, což je mez únavy pro konstantní rozkmit napětí při počtu cyklů ND = 5 × 106. Je-li Δσi ≥ ΔσD, pak m = 3. Prahový rozkmit napětí ΔσL odpovídá počtu cyklů NL = 108. Je-li ΔσL ≤ Δσi < ΔσD, má S-N křivka sklon m = 5. Rozkmity napětí Δσi které jsou menší než ΔσL nepřispívají do vypočtené kumulace poškození. Variabilita křivky životnosti zde není uvažována. Poškození Db vyvolané aplikací jednoho bloku zatížení je při použití Palmgren-Minerovy hypotézy kumulace poškození počítáno podle vztahu:

| Tabulka 1 – Rozkmity jmenovitých napětí Δσi a jejich četnosti ni v jednom bloku zatížení | ||||
| stupeň | Δσi [MPa] | ni [cyklů/blok] | ||
| od | do | od | do | |
| 1 | 10 | 20 | 1600 | 6400 |
| 2 | 20 | 30 | 720 | 2880 |
| 3 | 30 | 40 | 480 | 1920 |
| 4 | 40 | 50 | 400 | 1600 |
| 5 | 50 | 60 | 400 | 1200 |
| 6 | 60 | 70 | 375 | 1125 |
| 7 | 70 | 80 | 350 | 1050 |
| 8 | 80 | 90 | 300 | 900 |
| 9 | 90 | 100 | 250 | 750 |
| 10 | 100 | 110 | 200 | 600 |
| 11 | 110 | 120 | 150 | 450 |
| 12 | 120 | 130 | 100 | 300 |
Mezní poškození je reprezentováno deterministickou hodnotou DM =1. Rezerva spolehlivosti Z může být vyjádřena jako Z = R - S, kde R je odolnost spoje a S je účinek zatížení. V posuzovaném případě tedy například:
Z = R - S = DM - b × Db (3)
kde b je počet opakování jednoho bloku zatížení. Zde naznačený postup, včetně uvážení náhodnosti počtu cyklů ND a variability mezního poškození DM, lze nalézt v pracích Miloše Vlka [6, 7] a v kapitole 11 od téhož autora v knize [4].
Vlastní pravděpodobnostní posouzení doby života svarového spoje je provedeno metodou SBRA pomocí programu Anthill. Podrobnosti o této metodě a citovaném programu jsou v knihách Marek P. et al [4, 5] a na adrese www.sbra-anthill.com. Posudek je vztažen k S-N křivkám únavové pevnosti pro rozkmity normálových napětí, které odpovídají 95% pravděpodobnosti přežití hodnoty log N.
Posouzení podle jmenovitého napětí a kategorie detailu
U konstrukčního detailu podle obr. 3 se požaduje posouzení na únavu na porušení v kořeni svaru a na porušení v přechodu svaru do základního materiálu.
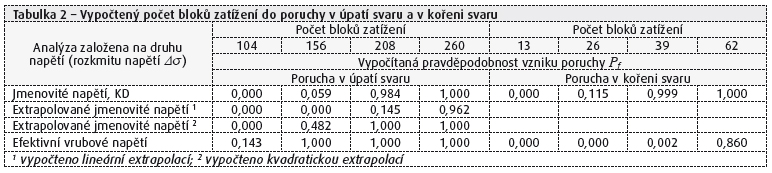
Posouzení na únavu na porušení v kořeni svaru se provádí za použití kategorie detailu 36. Mez únavy pro konstantní rozkmit napětí ΔσD = 26,14 MPa při ND = 5 × 106 cyklů, prahový rozkmit napětí ΔσL = 14,36 MPa při počtu NL = 108 cyklů. S použitím programu Anthill byly nalezeny histogram a distribuční funkce počtu bloků zatížení podle tabulky 1 do dosažení výše definovaného mezního stavu poškození a pro zvolené počty bloků 13; 26; 39; 52 byla vypočtena pravděpodobnost porušení Pf. Výsledky jsou uvedeny v obr. 6 a v tabulce 2.
Posouzení na únavu na porušení v přechodu svaru do základního materiálu se provádí pro rozkmit napětí Δσ v nosném plechu za použití kategorie detailu 63. Mez únavy pro konstantní rozkmit napětí ΔσD = 46,49 MPa při ND = 5 × 106 cyklů, prahový rozkmit napětí ΔσL = 25,54 MPa při počtu NL = 108 cyklů. S použitím programu Anthill byly nalezeny histogram a distribuční funkce počtu bloků zatížení podle tabulky 1 do dosažení výše definovaného mezního stavu poškození a pro zvolené počty bloků 104; 156; 208; 260 byla vypočtena pravděpodobnost porušení Pf. Výsledky jsou uvedeny v obr. 7 a v tabulce 2.
Posouzení při použití metody extrapolovaných jmenovitých napětí
Křížový spoj podle obr. 3 se posuzuje pro případ kdy se trhlina iniciuje z přechodu koutového svaru do základního materiálu za použití kategorie detailu 90, viz [1, 2]. Mez únavy pro konstantní rozkmit napětí ΔσD = 65,67 MPa při ND = 5 × 106 cyklů, prahový rozkmit napětí ΔσL = 36,07 MPa při počtu NL = 108 cyklů. V posudku není zahrnuta iniciace únavy z kořene svaru, následovaná růstem trhliny přes nebezpečný průřez svaru.
Extrapolované jmenovité napětí σhs je počítáno z napětí v referenčních bodech pomocí (a) lineární extrapolace, vyšlo (σhs/σnom) = 1,3012, (b) kvadratické extrapolace, vyšlo (σhs/σnom) = 1,4649, když σnom = σ1, viz obr. 3.
S použitím programu Anthill byly nalezeny histogram a distribuční funkce počtu bloků zatížení podle tabulky 1 do dosažení výše definovaného mezního stavu poškození a pro zvolené počty bloků 104; 156; 208; 260 byla vypočtena pravděpodobnost porušení Pf. Výsledky jsou v tabulce 2.
Posouzení při použití efektivního vrubového napětí
Metoda umožňuje posoudit jak úpatí svaru, tak i případ iniciace trhliny z kořene svaru. Pro únavové posouzení se v tomto případě použije jedna univerzální S-N křivka. Podle doporučení [2] je to pro ocel křivka únavové pevnosti KD 225, potom je mez únavy pro konstantní rozkmit napětí ΔσD = 165,78 MPa při ND = 5 × 106 cyklů a prahový rozkmit napětí ΔσL = 91,06 MPa při počtu NL = 108 cyklů. Únavová odolnost se týká stavu po svaření, je zahrnut vliv zbytkových napětí po svařování. Výsledky výpočtu efektivního vrubového napětí pro svarový spoj podle obr. 3 jsou v obr. 5. Pro vrub v kořeni svaru vyšlo (σnotch/σnom) = 5,4664 a pro vrub v úpatí svaru (σnotch/σnom) = 4,1204.
S použitím programu Anthill byly nalezeny histogram a distribuční funkce počtu bloků zatížení podle tabulky 1 do dosažení výše definovaného mezního stavu poškození a pro zvolené počty bloků zatížení 13; 26; 39; 52 byla vypočtena pravděpodobnost porušení Pf pro případ iniciace únavy z kořene svaru. Výsledky jsou uvedeny v tabulce 2. Analogické výsledky výpočtu pro případ iniciace trhliny v úpatí svaru jsou pro počty bloků zatížení 104; 156; 208; 260 rovněž uvedeny v tabulce 2.
V tomto příspěvku jsou bohatě využity poznatky autorů publikované v článcích [8, 9].
Souhrn a závěry
Prakticky všechny veličiny, které vstupují do posudku únavové životnosti, mají výrazně náhodný charakter. V tomto příspěvku je částečně respektována variabilita reálných provozních podmínek variabilitou četnosti výskytu rozkmitů napětí a variabilitou rozložení rozkmitů napětí pomocí omezených histogramů. Vlastní posouzení únavové životnosti je provedeno metodou SBRA s využitím programu Anthill. Výsledkem jsou histogramy a distribuční funkce počtu bloků zatížení do dosažení definovaného mezního stavu a vypočítané pravděpodobnosti vzniku poruchy Pf pro předem definované počty bloků zatížení. Výsledky se značně liší v závislosti na způsobu hodnocení účinků únavového působení, jak je zřejmé ze shrnutí výsledků v tabulce 2. Tyto rozdíly ukazují, že lze snadno dospět k nesprávnému hodnocení únavové životnosti svarového spoje, ať již zbytečně konzervativnímu, nebo naopak. Nicméně pravděpodobnostní přístup využívající metodu SBRA může, při důvěryhodných vstupních údajích, dát velmi dobrou představu o nárůstu kumulovaného poškození a o pravděpodobnosti poruchy v čase, vyjádřeném např. počtem zatěžovacích bloků.
Projekt byl realizován za finanční podpory projektu specifického výzkumu SP2011/157 Katedry pružnosti a pevnosti VŠB – TU Ostrava – Specifický vysokoškolský výzkum.
LITERATURA:
[1] ČSN EN 1993-1-9 (2006) Eurokód 3: Navrhování ocelových konstrukcí – Část 1-9: Únava
[2] Hobbacher, A. (2003): Recommendations for Fatigue Design of Welded Joints and Components. International Institute of Welding, doc. XII-1965-03/XV-1127-03, Paris, France, 2003
[3] Hobbacher, A. F. (2007): IIW odporúčaná metóda navrhovania konštrukcií proti únavovému poškodeniu, Zváranie-Svařování 56, 2007, č. 6–7, s. 167–173, ISSN 0044-5525
[4] Marek, P., Brozetti, J., Guštar, M., Tikalski, J. P. (2003): Probabilistic Assessment of Structures Using Monte Carlo Simulation, Background, Exercises, and Software. Second Edition, Institute of Theoretical and Applied Mechanics, Academy of Sciences of the Czech Republic, Praha 2003, CD ROM attached, ISBN 80-86246-19-1
[5] Marek, P., Guštar, M., Anagnos, T. Simulation-Based Reliability Assessment for Structural Engineers. Boca Raton, Florida: CRC Press, Inc., 1995, 365 p., 3,5“ diskette attached, ISBN 0-8493-8286-6
[6] Vlk, M. (2001): Uplatnění metody SBRA při řešení únavových problémů. In: Spolehlivost konstrukcí. Sborník referátů. II.ročník celostátní konference se zahraniční účastí. Ostrava, 21. 3. 2001, Dům techniky Ostrava, spol. s r. o. Ostrava 2001, ISBN 80-02-01410-3
[7] Vlk, M. (2005): Posouzení únavové životnosti metodou dílčích součinitelů a metodou SBRA, In: Spolehlivost konstrukcí. Sborník referátů. VI. ročník celostátní konference se zahraniční účastí, Ostrava, 6. 4. 2005, Dům techniky Ostrava, spol. s r. o. Ostrava 2005, ISBN 80-02-01708-0
[8] Václavek, L., Bárta, M. (2010): Účinky zatížení ve vztahu ke způsobu posouzení únavové odolnosti křížového svarového spoje. In: Guštar, M., Lokaj, A. ed. by (2010): Spolehlivost konstrukcí, Sborník referátů, XI. ročník celostátní konference se zahraniční účastí, Plzeň, 16. a 17. 4. 2010, Dům techniky Ostrava, spol. s r. o. Ostrava 2010, [CD-ROM], ISBN 978-80-02-02234-3
[9] Václavek, L., Bárta, M. (2010): Pravděpodobnostní posouzení únavové odolnosti křížového svarového spoje metodou SBRA, In: Guštar, M., Lokaj, A. ed. by (2010): Spolehlivost konstrukcí, Sborník referátů, XI. ročník celostátní konference se zahraniční účastí, Plzeň, 16. a 17. 4. 2010, Dům techniky Ostrava, spol. s r. o. Ostrava 2010, [CD-ROM], ISBN 978-80-02-02234-3
Probabilistic Approach to the Assessment of Fatigue Service Life of Welded Joints
Probabilistic fatigue life assessment of the cruciform joint with load-carrying fillet welds is executed using SBRA method. Variability of the frequency of occurrence for all stress ranges and variability of magnitudes of stress ranges is considered using bounded histograms. The results greatly differ depending on the assessment procedure of fatigue action. Probabilistic assessing using SBRA can give good idea regarding the growth of accumulative damage.