Pokročilé modely v požární bezpečnosti staveb

• Foto

V pracích o dynamické analýze plynů a konečných prvcích jsou ověřovací příklady pro uživatele i vývojáře programů integrálním součástí řešení. Lze nalézt odlišné názory na to, jak by ověřovací příklady měly být složité a zda by měly odkazovat pouze na analytická a numerická řešení nebo i experimentální data. Otázka souvisí s rozdíly mezi verifikací a validací. Při verifikaci se porovnává výpočetních řešení s přesnými analytickými nebo numerickými referenčními výstupy a mezi nimi. Při validaci se porovnává numerické řešení s experimentálními daty. Podle [1] lze ověřovací příklad ověřit testováním shody mezi numerickým řešením a čtyřmi ověřovacími postupy analytickým, přesným numerickým algebraickými ODE nebo diferenciálními PDE postupy a experimentem [2]. Na rozdíl od numerických řešení připravených pro validaci představují numerická řešení pro verifikaci matematické modely s jasným fyzikálním základem [1]. Numerickým modelům pro srovnání mezi analytickými a numerickými modely předchází validace [3].

Pro ověření programu i jeho správného použití se připravují ověřovací příklady. Význam databází, které shromažďují dobře zdokumentované ověřovací příklady pro zlepšení spolehlivosti numerických řešení, byl doložen například v [2]. Nejznámějším klasickým zdrojem je National Agency for Finite Element Methods and Standards (NAFEMS) s přibližně 280 ověřovacími příklady [4]. Některé komerční programy, jako jsou ANSYS a ABAQUS, přináší sady dobře zdokumentovaných testů. Například ABAQUS ve třech příručkách poskytuje širokou škálu ověřovacích příkladů (včetně 93 z NAFEMS) od jednoduchých jednoprvkových testů až po složité inženýrské problémy validované experimenty [5]. Tyto ověřovací příklady obsahují vstupní soubory, které pomáhají uživatelům při řešení jejich otázek.

VALIDACE

Experimenty

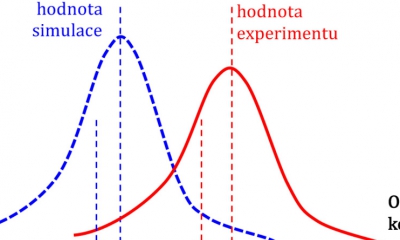
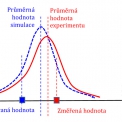
Pravděpodobnostní rozdělení výsledků experimentů výrazně ovlivňuje validaci každého modelu. Obr. 2 popisuje případ, ve kterém se při deterministickém řešení vybere na dvojici hodnot představujících odezvu. Experimentální data mají stochastickou povahu a popsují se distribucí pravděpodobnosti. Pro úplné porovnání je třeba výsledky prezentovat pravděpodobnostním způsobem s využitím distribuce pravděpodobnosti. Počítá se opakovaně s proměnou vybraných vstupních dat, která se mění podle simulace pravděpodobnosti. Takové rozsáhlé výpočty lze provádět automaticky pomocí specializovaných optimalizačních balíčků (např. LS-OPT^®, HyperStudy^® nebo ModeFrontier^®), které jsou zahrnuty v dnešních komerčních výpočetních systémech. Obr. 1 ukazuje případ, kdy číselný model velmi dobře předpovídá experiment s rozložením pravděpodobnosti v blízkosti zvoleného experimentu. Obr. 2 představuje opačnou situaci pro stejnou dvojici hodnot odezvy. Oba obrázky ukazují, že deterministické srovnání pouze dvou veličin může být problematické. Nemusí vypovídat o prediktivních schopnostech numerického modelu.

Kalibrace

Chování materiálu se do výpočtu zavádí materiálovým modelem, který popisuje mechanické a teplotní charakteristiky. Materiálový model je třeba kalibrovat, tak aby data odpovídala při modelu experimentu skutečně změřeným materiálovým hodnotám a v návrhovém modelu požadovaným charakteristickým hodnotám. V literatuře o verifikaci a validaci [2] je kalibrace modelu nepřijatelné řešení, kterého je při numerickém modelování třeba vyvarovat. Kalibrace ve výpočtu znamená neodůvodněnou úpravu vstupních dat použitých pro numerický model, aby se numerické výsledky posunuly blíže k experimentálním datům. Nesrovnalost mezi experimentem a numerickou simulací jsou často způsobeny některými neidentifikovanými vstupními parametry a manipulací se vstupními daty se generuje chybné řešení. Zlepšit model kalibrací lze pouze pro úplný stochastický popis experimentálních dat při pravděpodobnostní analýze simulace úpravou fyzikálního modelu pomocí několika různých simulovaných událostí.

VERIFIKACE

Studie citlivosti

Studie citlivosti je nepostradatelnou částí numerické analýzy. Proměnné ve studii ověří citlivost na všechny vstupy tak, aby bylo jasné, které jsou podstatné a jak, které mají přibližně lineární odezvu a které jsou zanedbatelné. Jako u analytické studie vychází studie citlivosti numerických modelů z matice vstupních dat. Volí se jedna vstupní hodnota a pro ostatní se volí hodnota střední.

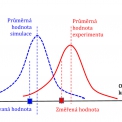
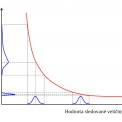
Rozlišení odezvy systému závisí na rozdílu vstupních parametrů a jejich rozsahu. Při návrhu ověřovacích testů je třeba brát v úvahu i nelinearitu reakce. Numerické experimenty se volí, aby přiměřená změna vstupních dat přinesla přiměřenou změnu odezvy systému. Obr. 3 přináší dva případy, kdy stejná odchylka ve vstupních datech způsobuje díky rozdílného rozložení odezvy rozdílné výsledky. Studie citlivosti příkladu s více proměnnými vstupními parametry pomáhá regresní analýza a uvažování rozptylu vstupních hodnot.

Ověřovací příklad

Správný ověřovací příklad má být jednoduchý a snadno pochopitelný [6] a [7]. Složitější příklad přináší méně spolehlivé ověření. Odpovědi na složité otázky, například pro pokročilé modely materiálu oceli nebo betonu, lze získat pouze numerickým řešením. Srovnání numerických řešení různých softwarových nástrojů ukazuje často neočekávaný nesoulad mezi výsledky. Podobné výsledky se nepovažují za silný důkaz spolehlivosti řešení. Dvě různá numerická řešení lze porovnat pouze na základě analýzy citlivosti řešení.

Při hledání jednoduchosti příklad nemusí nutně vycházet z otázek praxe. Slouží k ověření výpočetních modelů, které nevyřeší technický problém. Kritická je volba modelu materiálu. Materiálové modely skutečných konstrukčních materiálů se všemi požadovanými nelinearitami umožňují pouze přibližná řešení. Najít vhodnou rovnováhu mezi jednoduchostí a praktickým uplatněním řešeného příklad je obtížné. K řešení slouží hierarchický přístup. Připraví se soubor ověřovacích příkladů, od jednoduchých s analytickým řešením po složitější bližší k praxi. Součástí ověřovacího příkladu jsou úplná vstupní data, která jsou přehledně doložena. Všechny předpoklady, jako jsou vlastnosti materiálu, okrajové podmínky, rozložení teploty, zatížení, velké/malé deformace a posunutí, musí být jasně identifikovány. Pro experimentální příklady by měly být uvedeny všechna měření a podrobný popis zkušebního postupu.

Numerické ověřovací příklady vždy obsahují studii citlivosti volby sítě, která prokáže asymptotickou konvergenci. Na nejméně třech řešeních se dokládá vhodná přesnost zvoleného dělení na prvky. Pro výpočty metodou konečných prvků se doporučuje ověřit Grid Convergence Index (GCI), která využívá Richardsonovu extrapolaci [8]. Při ověření lze využít i jiných prvků, např. prvků 3D pro ověření prvků 2D nebo prvků s integrací ve více bodech.

NUMERICKÉ EXPERIMENTY A NÁVRHOVÉ MODELY

Vědecké a návrhové modely

V oblasti stavební praxe se výrazně oddělily modely zaměřené na vědecké poznání. Využívá se co nejpřesnějšího popisu chování materiálu s využitím popisu zúžení vzorku při tahové zkoušce, pro ocel např. Cauchy (true) stress a logarithmic (true) strain, a modelů porušení s více parametry. Přesný popis chování se využívá k přípravě numerických experimentů, které lze při návrhu konstrukce využít jako fyzických experimentů.

Modely zaměřené na navrhování konstrukcí naopak důsledně využívají jednoduché materiálové modely, které jsou popsány v návrhových normách pro jednotlivé materiály a které jsou historicky inženýrskou praxí ověřeny v analytických modelech. Návrhové modely využívají ověřené postupy návrhových norem, které pro jednotlivé klasifikují případy a podle klasifikace doporučují prutové nebo deskostěnové modely s využitím lineární analýzy, lineární stability, nelineární analýzy s a bez imperfekcí obvykle v oblasti malých deformací.

Koncepce mezních stavů

Současné návrhové normy využívají koncepce mezních stavů EN1990:2002 [9]. Koncepce umožnuje probabilisticky zajistit společensky požadované riziko selhání navrhované konstrukce. Přednostně se využívají dílčí součinitele spolehlivosti, které pro levou stranu rovnice spolehlivosti, pro odezvu konstrukce od zatížení, zavádí dílčí součinitele spolehlivosti zatížení a pro pravou stranu, pro únosnost konstrukce, zavádí dílčí součinitele spolehlivosti materiálu a konstrukčních prvků. Lze využít i návrh
úplným pravděpodobnostním výpočtem. Ten se obecně považuje za nejpřesnější, ale také za nejnebezpečnější. Pravděpodobnostní charakteristiky vstupů a jej citlivost na návrh není známa a u složitých modelů může vézt k nepřijatelným pochybením. Dílčí součinitele spolehlivosti naopak při rozvoji modelování zahrnují stoleté inženýrské poznatky praxe.

Numerické modely lze v metodě konečných prvků využít pro numerické experimenty a z výsledků numerických experimentů stanovit návrhové hodnoty postupy připravené pro mechanické experimenty. Návrhové modely lze zavedením dílčích součinitelů spolehlivosti materiálu přímo využít k návrhu konstrukce podle návrhových norem.

POKROČILÉ MODELY PRO POŽÁRNÍ BEZPEČNOST STAVEB

Otázky týkající se bezpečnosti, včetně požární bezpečnosti, jsou v Evropské unii řešeny na národní úrovni a právní požadavky jsou určeny předpisy jednotlivých zemí. Požární bezpečnost je kulturním bohatstvím jednotlivými zeměmi liší a politická motivace tohoto řešení je běžné, že podobné otázky musí být znovu prozkoumány a odpovězeny v jednotlivých zemích. V kontextu Evropské unie jako celku jsou požadavky na požární bezpečnost založeny v nařízení EU č. 305/2011. Dokument Evropského parlamentu a Rady stanoví harmonizované podmínky pro uvádění stavebních výrobků na trh jako základní požadavek na stavební práce [10]. V příloze I této směrnice jsou shrnuty základní požadavky na konstrukční odolnost a stabilitu a požární bezpečnost. Stavební práce musí být navrženy a zhotoveny tak, aby v případě výskytu požáru: nosnost konstrukce byla po požadovanou dobu zajištěna, rozvoj a šíření požáru a kouře uvnitř budovy bylo zabráněno, šíření požáru do sousedních nemovitostí bylo zabráněno, osoby mohly opustit budovu nebo se zachránit jinými možnostmi a byla zajištěna bezpečnost při práci záchranných týmů.

Zatímco požadavky jsou národní, pro jejich zajištění se využívá mezinárodních znalosti v evropských/celosvětových experimentálních a návrhových normách. Požáry se považují za první mimořádné zatížení a požadavky na jejich modelování i obecné zásady pro použití pokročilých modelů jsou shrnuty EN1991-1-2:2002 [11]. Přestup tepla do konstrukce a návrh konstrukce je předmětem jednotlivých materiálově orientovaných norem EN199x-1-2:200x. K problematice Validace a verifikace v požárním navrhování byly připraveny mezinárodní normy ISO/TR 15656:2003 [12] a ISO/FDIS 16730:2008 [13].

SHRNUTÍ

Před čtyřmi desetiletími byly numerické modely považovány za hypotetickou možnost přípravy experimentů, které budou replikovat skutečnost. O dvě desetiletí později se již jednalo o široce přijímané rozšíření experimentální a teoretické práce. Dnešní výpočetní analýza, zejména numerická mechanika a dynamika tekutin, se běžně používá jako nepostradatelný návrhový nástroj a katalyzátor mnoha relevantních oblastí výzkumu. Vývoj moderního univerzálního softwaru a snižování nákladů na výpočetní prostředky vývoj výrazně usnadnily a zpřístupnily pro aplikovaný výzkum.

Výpočetní nástroje se v praxi staly snadněji dostupnými a použitelnými, i pro relativně nezkušené inženýry. Využívání numerické analýzy musí být spojeno s kontrolou výsledků. Jediný způsob, jak dokázat správnost simulovaných výsledků, je proces metodické validace a verifikace. Bez něj nemůže být analýza použita pro rozhodování. V případě, že je analyzovaná skutečnost příliš složitá nebo příliš drahá na experimentální ověření je na místě hierarchie verifikace. V případě mimořádných událostí, jako je šíření požáru ve vícepodlažní budově, její prostorové zhroucení nebo reakce na výbuch, experimentální výsledky nemohou být k dispozici. Validace modelů není reálná. Zajistit správné a věrohodné výsledky lze pouze správnou volbou validace a verifikace.

Na přípravu metodiky ověření pokročilých modelů v požární bezpečnosti staveb je zaměřen projekt Ministerstva vnitra VI20162019034, který již příští rok nabídne vhodná řešení pro požární praxi a státní správu.

OZNÁMENÍ

Autoři vzpomínají s obdivem na kolegu Leslawa Kwasniewskeho, který po dlouhé nemoci 11. října 1014 zemřel. Článek vychází z jeho práce v projektu COST TU0904 IFER a článku (Kwasniewski 2008) [13] a (Wald at al, 2014) [14]. Příspěvek byl vypracován v rámci práce na projektu MV ČR VI20162019034.

REFERENCE:
[1] AIAA, Guide for the Verification and Validation of Computational Fluid Dynamics Simulations, American Institute of Aeronautics and Astronautics, AIAA-G-077-1998, Reston, VA, 1998.
[2] Oberkampf W.L., Trucano T.G., Verification and validation benchmarks, Nuclear Engineering and Design 238, 716–743, 2008.
[3] ASME Guide for Verification and Validation in Computational Solid Mechanics, The American Society of Mechanical Engineers, 2006.
[4] NAFEMS, National Agency for Finite Element Methods, http://www.nafems.org/, 2013. 
[5] SIMULIA, Abaqus 6.11 Benchmarks Manual, © Dassault Systèmes, 2011.
[6] Wald F., Burgess I., Kwasniewski L. Horová K. et al, Benchmark studies, Verification of numerical models in fire engineering, Praha, CTU Publishing House, 2011.
[7] Wald F., Burgess I., Kwasniewski L. Horová K. et al, Benchmark studies, Experimental validation of numerical models in fire Engineering, Praha, CTU Publishing House, 2011.
[8] Roache, P. J. Verification and Validation in Computational Science and Engineering, Computing in Science Engineering, Hermosa Publishers, 1998.
[9] EN 1990:2002 Eurocode – Basis of structural design, CEN Brussels, 2002.
[10] Regulation (EU) No 305/2011 of the European Parliament and Council, Harmonised conditions for the marketing of construction, 2011, URL: eur-lex.europa.eu.
[11] EN 1991-1-2, Eurocode 1: Actions on structures – Part 1-2: General actions – Actions on structures exposed to fire, CEN Brussels, 2002.
[12] ISO, Guide to the Expression of Uncertainty in Measurement, ISO, Geneva, 1993.
[13] ISO/FDIS 16730 Fire safety engineering — Assessment, verification and validation of calculation methods, Geneva, 2008.
[14] Kwaśniewski, L., On practical problems with verification and validation of computational models, Archives of Civil Engineering, 55, 3, 2009, 323 – 346.
[15] Gillie M., Author‘s Analysis of heated structures: Nature and modelling benchmarks, Fire Safety Journal 44, 673 – 680, 2009.

Autoři

• Prof. Ing. Wald František CSc.
• Ing. Cábová Kamila Ph.D.