Parametrické modely požáru pro EN 1991‑1‑2:2021

• Foto

V současné době jsou připravovány změny, které by měly být do Eurokódu zavedeny. Vzhledem k tomu, že v některých zemích nebyla metoda přílohy A schválena, nabízí se otázka, jaké nedostatky současná parametrická teplotní křivka má a zda některá z národních příloh evropských států nepopisuje parametrický požár přesněji. Tento článek je zaměřen na porovnání parametrických teplotních křivek podle současné přílohy A [1], německé národní přílohy [2] a podle dánské národní přílohy [3]. Porovnání bylo autory článku připraveno jako podklad pro pracovní skupinu CEN TC 250/SC 1/WG 4.

PROBLEMATIKA PARAMETRICKÉ TEPLOTNÍ KŘIVKY V SOUČASNÉ PŘÍLOZE A

Současný parametrický model požáru v příloze A Eurokódu vychází ze švédské křivky. Tato křivka byla poprvé publikována v roce 1970 (Magnusson a Thelandersson) [4]. Parametrická teplotní křivka využívá na rozdíl od nominálních teplotních křivek pro popis okrajové podmínky zkoumaného požárního úseku. Předpokladem této křivky je, že teplota plynu je rovnoměrně rozložena v celém zkoumaném úseku. Omezuje se na použití do 500 m² podlahové plochy s maximální výškou požárního úseku 4 m, bez otvorů ve střeše. Další omezení se týká obvodových konstrukcí (koeficient b), otvorů v nich (koeficient O) a hustoty požárního zatížení (qt,d). Pokud je hustota požárního zatížení stanovena bez zvláštních úvah o chování při hoření, pak se má postup omezit na požární úseky s požárním zatížením převážně typu celulózy [1].

Obecný tvar parametrické křivky dle přílohy A zobrazuje obr. 1A. Část křivky reprezentující ohřev se vyznačuje exponenciálním nárůstem, který končí v hodnotě maximální teploty označené jako Θ_max (v čase t*_max). Po dosažení maximální teploty začíná fáze s lineárním poklesem, která končí v okamžiku, kdy se teplota ve zkoumaném úseku dostane na 20 °C (tedy na předpokládanou teplotu okolního prostředí).

Příloha A Eurokódu 1 nebyla v mnoha zemích schválena. Země poukazují na různé problémy spojené s parametrickou teplotní křivkou, která v některých případech poskytuje nereálné zvýšení a snížení teploty v požárním úseku. Například pro obytné a administrativní prostory je stanovena hodnota maximální teploty v čase 20 minut. Pro požární prostory s velkými otvory a obalovými konstrukcemi s nízkou tepelnou vodivostí poskytuje Eurokód extrémně rychlý nárůst a následný pokles teploty. Naproti tomu je ovšem pro požární prostory s malými otvory a vysokou tepelnou vodivostí obalových konstrukcí předpokládán extrémně pomalý pokles teploty [6].

Parametrická teplotní křivka v současném Eurokódu popisuje pouze plně rozvinutou fázi požáru, bez zohlednění růstové fáze. Provedenými požárními zkouškami s obyčejným nábytkem ovšem bylo dokázáno, že i v malých prostorech může trvat několik minut, než se od počáteční fáze dosáhne plně rozvinutého požáru [5].

Některé země považují za kritický bod to, že parametrická teplotní křivka v současné příloze A nemá přímou souvislost s rychlostí uvolňování tepla. Touto problematikou se zabývají například články [5, 6], které poukazují na nesoulad mezi časovým průběhem parametrické teplotní křivky a rychlostí uvolněného tepla.

Většina návrhů parametrických teplotních křivek vychází z experimentálních výsledků, a proto je jejich rozsah použití omezen na rozměry, požární zatížení a další faktory podobné těm v příslušných požárních zkouškách. Pro použití v moderní architektuře, je v současné Příloze A zvláště důležité omezení koeficientu povrchů, který je závislý na tepelné pohltivosti konstrukcí ohraničujících požární úsek b < 100; 2 200 > [J/(m²s^1/2K)]. Tímto omezením totiž zaniká možnost využití parametrické teplotní křivky například pro výpočet teploty plynu v úseku se skleněnou fasádou [7].

S nejvyšší pravděpodobností nebude ani do budoucna možné předepsat parametrickou teplotní křivku tak, aby byla použitelná pro všechny požární úseky. S ohledem na vývoj materiálů a konstrukcí, by bylo alespoň potřeba oblast použití parametrické teplotní křivky uvedené v Eurokódu rozšířit. Je to důležité jak pro současnost, tak pro budoucí požární navrhování.

DALŠÍ PARAMETRICKÉ TEPLOTNÍ KŘIVKY

Parametrické teplotní křivky se vyvíjely empiricky, na základě výsledků získaných při požárních zkouškách. Kromě křivky, která je uvedena v současném Eurokódu, existuje řada dalších parametrických teplotních křivek.

V 70. letech 20. století publikovali Magnusson a Thelendersson křivky, založené na konvenčních rovnicích rovnováhy hmotnosti a energie. Tyto křivky, které jsou začleněny do švédských norem, poskytly základ parametrické teplotní křivce v současném Eurokódu [8].

Určité zjednodušení výpočtu nabízejí křivky nazvané BFD. Oproti parametrické teplotní křivce dle přílohy A, kde je potřeba dvou rovnic pro výpočet fáze růstu a fáze poklesu, u BFD křivek popisuje celý průběh (ohřev i ochlazování) pouze jedna rovnice. Část křivky s ochlazováním je popsána nelineárně a tedy realističtěji. Tyto křivky, které jsou používány v Austrálii, vznikaly za pomoci dat získaných z více než 142 zkoušek přirozeného požáru za přispění práce C. R. Barnetta z Nového Zélandu [9]. Jeho motivací bylo představit alternativu k parametrické teplotní křivce uvedené příloze A Eurokódu 1.

V dánské národní příloze k Eurokódu lze najít úpravu pro výpočet parametrické teplotní křivky (dále jen dánské křivky), kde je teplota v požárním úseku popsána právě jednou rovnicí pro celý průběh požáru. Omezení, kdy lze křivku použít, zůstává ovšem obdobné jako v současné příloze A.

Další alternativou k současné příloze A je takzvaná parametrická požární křivka iBMB (název vychází z Institut für Baustoffe, Massivbau und Brandschutz TU Braunschweig). Tuto křivku předložili v roce 2003 němečtí výzkumní pracovníci Jochen Zehfuss a Daniela Hosser a v současné době je postup výpočtu obsažen v německé národní příloze k Eurokódu. Německá křivka se vyznačuje hlavně tím, že je přímo odvozena z rychlosti uvolňování tepla a je charakterizována třemi body, ve kterých se mění sklon křivky [6]. Tato křivka také dokáže zohlednit účinek flashover efektu, kdy v růstové fázi dojde k prudkému nárůstu teploty ve zkoumaném úseku.

Na obr. 1 je vidět schematický tvar parametrické teplotní křivky obsažené v současné Příloze A a zároveň i průběh křivek alternativních (dánská, německá).

POROVNÁNÍ PARAMETRICKÝCH TEPLOTNÍCH KŘIVEK

V současné době probíhá v pracovní skupině CEN TC 250/SC 1/WG 4 diskuze nad úpravou přílohy A Eurokódu 1, jejíž finální verze bude součástí nových Eurokódů po roce 2021. Jako podklad pro diskuzi vypracovali autoři článku porovnání parametrických teplotních křivek podle současné přílohy A [1], německé národní přílohy [2] a podle dánské národní přílohy [3]. Pro porovnání jednotlivých průběhů parametrických teplotních křivek vůči průběhům teplot pozorovaných při požárních zkouškách, byla vytvořena databáze obsahující data z uskutečněných zkoušek z ČR i ze zahraničí (celkem z 25 velkorozměrových zkoušek). Vzhledem k omezením, které jednotlivé parametrické křivky mají, však nelze aplikovat všechny výpočty na všechny požární zkoušky. 

V databázi jsou pro každou zkoušku zaznamenány teploty plynu v časovém průběhu požáru. Za pomoci zautomatizovaných výpočetních postupů v tabulkovém procesoru jsou s využitím dostupných vstupních dat na tyto zkoušky aplikovány jednotlivé výpočetní postupy parametrické teplotní křivky podle současné přílohy A [1], německé národní přílohy [2] a dánské národní přílohy [3]. Vstupní data obsahují informace o rozměrech požárního úseku, ventilačních otvorech (rozměry, počet), materiálu obvodových konstrukcí a použitém požárním zatížení. Ve výpočetních souborech je sledován průběh teploty v čase pro jednotlivé požární křivky, které jsou pro efektivní porovnání pro jednotlivé požáry vykresleny do jednoho grafu společně se skutečně naměřenou teplotou plynu z požární zkoušky. Níže jsou jako příklad uvedeny výsledky výpočtů provedené pro požární zkoušku z Cardingtonu a zkoušku z VTT ve Finsku.

APLIKACE KŘIVEK NA POŽÁRNÍ ZKOUŠKU V CARDINGTONU

Požární zkouška proběhla ve Velké Británii, v Cardingtonu. Při zkoušce č. 6 byl simulován požár kanceláře. Budovu tvořil osmipodlažní ocelový skelet se spřaženými ocelobetonovými stropy (viz obr. 2A). Stěny byly tvořeny pórobetonovými tvárnicemi, podlaha byla betonová. Rozměry požárního úseku byly 7,5 × 18,0 × 4,0 m (šířka × délky × výška). V úseku se nacházel jeden ventilační otvor o rozměrech 18,0 × 2,0 m (šířka × výška). Požární zatížení (q_t,d = 159 MJ/m²) se skládalo z nábytku, dřeva a kancelářských potřeb [10].

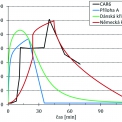
Na obr. 3 jsou uvedeny výsledky aplikace všech tří parametrických teplotních křivek – křivka podle přílohy A Eurokódu 1, křivka podle dánské národní přílohy a křivka podle německé národní přílohy, společně s teplotou plynu, která byla naměřena během experimentu.

Z porovnání na obr. 3 je patrné, že křivka podle německé národní přílohy téměř přesně vystihuje maximální teplotu, naměřenou při požární zkoušce (v grafu označeno jako CAR6). Teploty se v počáteční fázi německé křivky velice odlišují od reality (jsou velice nízké). Skutečně naměřené hodnoty ukazují velice strmý nárůst teploty v přibližně 10. min. Těchto teplot je v křivce dosaženo až při vzniku flashover efektu, přibližně o 10 min později (cca 20. min).

V případě parametrické teplotní křivky dle současné přílohy A a zároveň i křiky podle dánské národní přílohy je opět na obr. 2 vidět, že v době, kdy se skutečně naměřené hodnoty pohybují okolo svého maxima, jsou teploty v těchto křivkách velice nízké, nebo dokonce již na hodnotě teploty okolí (20 °C). Většina požárního zatížení vyhoří v obou případech již průběhu prvních 30 min, což je ale oproti realitě velice odlišné.

APLIKACE KŘIVEK NA POŽÁRNÍ ZKOUŠKU VE FINSKU

Požární zkouška proběhla ve Finsku, v Centru technického výzkumu (VTT). Stěny byly betonové, stejně tak i stropní konstrukce. Podlaha byla tvořena žáruvzdornými tvárnicemi. Rozměry požárního úseku byly 2,2 × 4,0 × 2,6 m (šířka × délky × výška). V úseku se nacházel jeden malý ventilační otvor o rozměrech 3,0 × 1,2 m (šířka × výška). Požární zatížení (q_t,d = 152 MJ/m²) se skládalo z dřeva [11].

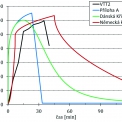
Na obr. 4 je zobrazeno porovnání všech tří parametrických teplotních křivek – křivka podle přílohy A Eurokódu 1, křivka podle dánské národní přílohy a křivka podle německé národní přílohy, společně s teplotou plynu, která byla naměřena během experimentu.

Na obr. 4 je vidět, že parametrická teplotní křivka podle německé národní přílohy je zde na straně bezpečnosti a to jak ve fázi růstu, tak i ve fázi poklesu teplot. Hodnoty maximálních teplot se velice podobají skutečně získaným hodnotám (do 100 °C). Fáze poklesu začíná přibližně o 10 min později než je tomu ve skutečnosti.

Na obr. 4 je rovněž možné pozorovat, že průběhy parametrické teplotní křivky dle Přílohy A a dle dánské národní přílohy jsou v počáteční růstové fázi téměř totožné. U parametrické teplotní křivky dle Přílohy A začíná fáze poklesu skoro o 15 min dříve než je tomu ve skutečnosti. Požár tedy skončí ještě dříve, než je ve skutečně naměřených hodnotách dosaženo maximální teploty. Obdobně je tomu i u dánské křivky, která začíná klesat ještě dříve, ale pozvolněji. V případě, že by byly křivky dále použity na posuzování požární odolnosti, je možné, že budou hodnoty nepoužitelné, především pro křivku dle současné Přílohy A.

ZÁVĚR

Z provedeného porovnání v celkovém počtu 25 požárů vyplývá, že křivka podle německé národní přílohy ve většině případů velice přesně popisuje průběh požáru. Ve většině případů je největší shody německé křivky a teplot naměřených při zkouškách dosaženo až po uplynutí přibližně 15 min. Do této doby požáru nemá stoupající fáze německé křivky tak intenzivní růst, jako je tomu při skutečně naměřených teplotách. Maximální teplota v požárním úseku je převážně přesně vystižena a to jak svoji hodnotou, tak časem, kdy je dosažena. Stejně tak se fáze poklesu ve většině případů velice podobá skutečnému průběhu. 

V případě křivky podle současné Přílohy A, respektive křivky podle dánské národní přílohy je popisován lépe průběh mezi začátkem požáru a cca 15 min. V této počáteční
fázi vykazují křivky strmější nárůst oproti německé křivce a ve většině případů se tak více podobají skutečnému průběhu teplot. Obě tyto křivky ale vykazují nereálné zvýšení, případně snížení teploty v požárním úseku v průběhu požáru.

V mnoha případech aplikace křivky dle současné Přílohy A dochází k tomu, že požár podle křivky skončí (teplota se dostane na teplotu okolí 20 °C) ještě dříve,

než je ve skutečně naměřených hodnotách dosaženo maximální teploty. Obdobně je tomu i u dánské křivky, která začíná mnohdy klesat ještě dříve, avšak pozvolněji.

Pokud je křivka dle současné Přílohy A, případně dánská křivka použita na posuzování požární odolnosti, mohlo by hrozit, že budou výsledné hodnoty převážně nepoužitelné (zejména pro křivku dle současné Přílohy A). Pro další konstatování bude nutné aplikovat parametrické teplotní křivky pro výpočet požární odolnosti a porovnat je se skutečnými hodnotami. Předběžně se zdá, že v případě využití německé křivky bude aplikace na straně bezpečnosti.

PODĚKOVÁNÍ

Autoři článku děkují Prof. Dr. Jochenu Zehfussovi a Lise Sander, M. Sc. z Technické univerzity v Braunschweigu (Institut für Baustoffe, Massivbau und Brandschutz (iBMB) TU Braunschweig), díky kterým byla databáze požárních zkoušek vytvořena. Výzkum byl podpořen grantem GACR 16-18448S.

LITERATURA:
[1] ČSN EN 1991‑1‑2 Eurokód 1: Zatížení konstrukcí – Část 1–2: Obecná zatížení – Zatížení konstrukcí vystavených účinkům požáru. 2004.
[2] DIN EN 1991‑1‑2/NA:2010‑12: National Annex – Nationally determined parameters – Eurocode 1: Actions on structures – Part 1–2: General actions – Actions on structures exposed to fire. 2014
[3] DS/EN 1991‑1‑2 DK NA:2014 National Annex to Eurocode 1: Actions on structures – Part 1–2: General actions – Actions on structures exposed to fire. 2014.
[4] PETTERSSON, O., S‑E. MAGNUSSON a J. THOR. Fire Engineering Design of Steel structures. 1976.
[5] ZEHFUSS, J. a D. HOSSER. A parametric natural fire model for the structural fire design of multi‑storey buildings. Fire Safety Journal [online]. 2007, 42(2), 115–126. ISSN 03797112. Dostupné z: doi:10.1016/j.firesaf.2006.08.004
[6] ZEHFUSS, J. Case studies of a new simplified natural fire model and safety concept for structural fire safety design. 2011
[7] HOROVÁ, K.. Modelling of fire spread in structural fire engineering: doctoral thesis = Modelování šíření požáru při navrhování konstrukcí. 2015.
[8] HOSSER, D. a J. ZEHFUSS. Fire Safety Design of Multi‑Storey Buildings for Natural Fires. B.m.: Technical University of Braunschweig, Germany.
[9] BARNETT C.F., BFD curve: a new empirical model for fire compartment temperatures, Fire Safety Journal, Vol. 37, Issue 5, 2002, Pages 437–463. Dostupné z doi:. 10.1016/S0379‑7112(02)00006‑1.
[10] O’CONNOR, M. A. a D. M. MARTIN. Behaviour of a multi‑storey steel framed building subjected to fire attack. Journal of Constructional Steel Research [online]. 1998, 46(1–3), 295. ISSN 0143974X. Dostupné z: doi:10.1016/ S0143‑974X(98)00122‑9.
[11] RANBY, A., T. INHA a J. MYLLYMÄKI. Structural Steel Fire Design. SBI Publication 134. Finish Constructional Steelwork Asssociation, Norwegian Steel Asssociation, Swedish Institute of Steel Construction. 2000. 

Autoři

• Kučera Jaroslav
• Ing. Cábová Kamila Ph.D.