Analýza předpjaté membrány ve tvaru mezikruží
Rubrika: Materiály
Článek se zabývá statickou analýzou předpjaté membrány ve tvaru mezikruží z lehkého konstrukčního betonu. Jsou zde vysvětleny pojmy jako výchozí stav nebo samokotvený systém. Na závěr jsou prezentovány účinky dotvarování a smršťování.
Předpjaté betonové membrány jsou konstrukce, jejichž použití ve stavební praxi má nezastupitelné místo a to nejen kvůli variabilnosti v typech zastřešení a možnosti překlenout plochy značných rozměrů, ale také díky jejich poměrně jednoduché výstavbě nevyžadující skruž a v neposlední řadě i nezanedbatelné úspoře materiálů. Patří mezi konstrukce plně odpovídající dnešní moderní době, kdy již není potřeba plnit pouze funkční požadavky zastřešení, ale také klást důraz na estetické působení a začlenění do urbanistického celku.
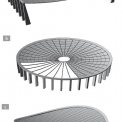
Konstrukční uspořádání a výstavba předpjatých membrán v podstatě vychází z řešení předpjatých pásů, které jsou běžné budované v mostním stavitelství při vytváření lávek pro pěší. Předpjaté membrány lze rozdělit do několika základních typů (obr. 1). Plně ekvivalentní pásům jsou střešní konstrukce ve tvaru válcové plochy, které se řadí mezi plochy s jednoduchou křivostí. Další skupinou zastřešení jsou plochy dvojí křivosti, mezi něž patří rotačně symetrické plochy nebo lanové sítě (známý hyperbolický paraboloid). Ty se již liší od předpjatých pásů svým prostorovým působením a větší tvarovou stálostí.
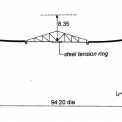
Tento článek je založen na studii a statické analýze předpjaté membrány nad kruhovým půdorysem s vnitřním prstencem, která může mít široké praktické využití. Nejvíce se pak nabízí využití při zastřešení tribun sportovních hal a stadionů. Na obr. 2 je schéma již realizovaného zastřešení. Jedná se o sportovní halu v Montevideu, která byla postavena v roce 1957 a řadí se mezi první visuté konstrukce z předpjatého betonu.
POPIS KONSTRUKCE
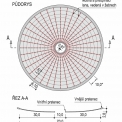
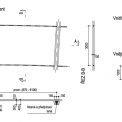
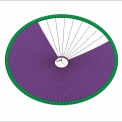
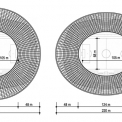
Studovaná rotačně symetrická konstrukce tvaru mezikruží je tvořena membránou z lehkého konstrukčního betonu, která je nesena, a následně také předepnuta, lany radiálně vedenými mezi obvodovými prstenci. Základní rozměry konstrukce jsou zobrazeny na obr. 3. Půdorysný průměr vnějšího prstence je 70 m a vnitřní prstenec zaujímá průměr 10 m. Šířka pásu betonové membrány je tedy 35 m. Radiálně vedená lana, která svírají konstantní středový úhel o velikosti 10 °, rozdělují membránu na 36 řad prefabrikovaných segmentů. Tvar segmentů v příčném řezu je zobrazen na obr. 4. Jedná se o desku tloušťky 100 mm, která je na radiálních hranách opatřena žebry výšky 400 mm, ve kterých jsou lana. Půdorysné rozmístění lan přímo souvisí s rozměry betonových segmentů, jejichž délka se pohybuje v rozmezí od 0,87 m do 6,1 m. Šířka segmentů je konstantní a má velikost 3,0 m.
Lana plní v konstrukci dvojí funkci. První skupinou jsou tzv. nosná lana, která jsou vedena mezi obvodovými prstenci a na která se při výstavbě pokládají prefabrikované segmenty. Každé žebro obsahuje šest nosných lan. Druhou skupinou lan jsou lana předpínací, kterými je do již zmonolitněné konstrukce vnesena tlaková rezerva, díky níž nevznikají v betonové membráně od proměnných zatížení nežádoucí tahová napětí. Každé žebro opět obsahuje šest předpínacích lan.
Konstrukce tvoří tzv. samokotvený systém, ve kterém jsou vodorovné síly z kotvení lan přenášeny do obvodových prstenců a vyvozují v nich tlaková (vnější prstenec) a tahová (vnitřní prstenec) namáhání. Ze způsobu namáhání vyplývá volba materiálů jednotlivých prvků, proto vnější prstenec je navržen jako železobetonový obdélníkový průřez a vnitřní prstenec tvoří ocelová trubka z konstrukční oceli (obr. 4).
POSTUP VÝSTAVBY
Nespornou výhodou předpjatých membránových střech je stejně jako u předpjatých pásů jejich postup výstavby, který dovoluje poměrně rychlé a na okolí téměř nezávislé zbudování konstrukce. Ze statického hlediska lze výstavbu konstrukce rozdělit do dvou hlavních fází, které obsahují několik dílčích kroků. Hraničním stavem mezi hlavními fázemi výstavby je tzv. výchozí (nebo též rovnovážný) stav, od kterého by měly začínat všechny výpočty.
V 1. fázi výstavby je provedena betonáž vnějšího prstence na svislých nosných prvcích a montáž vnitřního prstence na montážní plošině. Poté jsou mezi oběma obvodovými prstenci natažena nosná lana, na která je následně vnitřní prstenec zavěšen do požadované polohy. V dalším kroku jsou na lana pokládány a upevňovány betonové segmenty. Následně se do žeber osadí předpínací lana. Protože se tato fáze nachází před výchozím stavem, jsou při statické analýze jednotlivé dílčí kroky prováděny zpětně, tedy dochází k odlehčování konstrukce a konstrukce staticky působí jako zatížené lano.
Ve 2. fázi výstavby dojde k zalití spár mezi segmenty navzájem a také krajních spár u obvodových prstenců. Po dosažení dostatečné pevnosti výplně spár jsou dopnuta předpínací lana v žebrech na napětí cca 1 100 MPa tak, aby byla do membrány vnesena tlaková rezerva, která eliminuje tahová napětí v betonu od proměnných zatížení. V této fázi výstavby již konstrukce působí jako předpjatá membrána a ve statické analýze jsou jednotlivé dílčí kroky prováděny dopředně.
VÝPOČETNÍ MODEL
Statická analýza navržené předpjaté membrány je provedena pomocí prostorového výpočetního modelu vytvořeného ve FEM programu ANSYS (obr. 5). Vzhledem k charakteru konstrukce jsou výpočty prováděny geometricky nelineárně plnou Newton-Raphsonovou metodou. V modelu je zohledněn postup výstavby konstrukce a jsou použity standardní typy prutových a deskostěnových prvků.
Konstrukce je podepřena po obvodě vnějšího prstence v místech kotvení lan tuhými svislými vazbami a pružnými vodorovnými vazbami. Tím je umožněno volné stlačení vnějšího prstence účinkem normálové síly, vyvolané radiálním účinkem horizontálních složek kotevních sil z lan (viz samokotvený systém). Tento způsob podepření reprezentuje uložení zastřešení na spodní stavbu prostřednictvím ložisek.
VÝCHOZÍ (ROVNOVÁŽNÝ) STAV
Předpjaté membrány jsou konstrukce, jejichž hlavním nosným prvkem jsou lana. Betonové segmenty pak nejen plní funkci zastřešení, ale navíc značně přispívají ke zvýšení tuhosti a stability jinak ohybově měkké konstrukce. Prostorový tvar membrány je pak dán průvěsovými křivkami jednotlivých lan, která jsou zatížena vlastní tíhou konstrukce. Z hlediska statické analýzy lze průvěsové křivky lan získat nalezením tzv. výchozího (nebo též rovnovážného) stavu konstrukce. Jedná se o takovou fázi výstavby konstrukce, kdy betonové panely jsou volně zavěšeny na nosná lana, příp. jsou vyplněny spáry mezi jednotlivými segmenty, a vlastní tíha konstrukce je v rovnováze s radiálními účinky lana (proto termín rovnovážný). Od tohoto stavu by měly začínat všechny výpočty předpjaté membrány (proto termín výchozí). Řešením výchozího stavu je určení průvěsové křivky a napětí v laně od působícího zatížení. Po zadání stanovené geometrie lana a jeho napjatosti do výpočetního modelu a provedení výpočtu se správnost řešení projeví tím, že na konstrukci od působící vlastní tíhy budou svislé deformace blízké nule. Zatížení a radiální síly jsou tedy v rovnováze.
V případě konstrukce ve tvaru mezikruží jsou jednotlivá lana (za lano je považovaná skupina všech nosných lan vedených v jednom žebru) vedena radiálně mezi oběma prstenci a vlastní tíha panelů má tvar lichoběžníkového zatížení. Díky rotační symetrii a konstantnímu středovému úhlu jsou všechny řady segmentů stejné. Proto postačí vyšetřovat pouze jedno lano. Stanovená napjatost a průvěsová křivka je pak stejná pro všechna nosná lana v konstrukci.
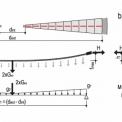
Řešením výchozího stavu zatíženého lana, jehož cílem je nalezení průvěsové křivky lana a jeho příslušné napjatosti, se zabývala řada autorů, např. Kadlčák [2]. Stanovení výchozího stavu konstrukce se provádí pomocí náhradního nosníku, který v případě mezikruží může bát zvolen dvěma způsoby. Prvním způsobem je řešení výchozího stavu na průběžném laně, zakotveném pouze do vnějšího prstence (vnitřní prstenec se „odstraní“), které je zatíženo složeným lichoběžníkovým zatížením a bodovou silou představující tíhu části vnitřního prstence (obr. 6a). Jedná se tedy o lano podepřené neposuvně v krajních bodech ve stejné výšce. Pak je rozpětí lana a tedy náhradního nosníku (L-d). Rovnice průvěsové křivky má tvar:
Druhým způsobem je řešení části konstrukce mezi vnějším a vnitřním prstencem (obr. 6b). Pak se jedná o lano s bodem volně posuvným ve svislém směru zatížené lichoběžníkovým zatížením a osamělou silou. Náhradním nosníkem je konzola a rovnice průvěsové křivky má tvar: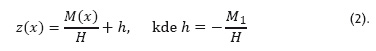
Tyto rovnice jsou odvozeny např. v Kadlčákovi [2]. Veličiny v rovnicích jsou: z(x) je z-ová pořadnice průvěsové křivky lana, M(x) je ohybový moment na náhradním nosníku od působícího zatížení, H je vodorovná složka tahové síly v laně, h je svislá vzdálenost mezi vnitřním a vnějším prstencem a M1 je ohybový moment ve vetknutí na konzole.
Při působení svislého zatížení je síla H (tedy vodorovná složka osové síly v lanech) konstantní po délce lana. Tato síla je však neznámá a nedá se stanovit pouze ze statických podmínek rovnováhy. Proto je nutné zavést jednu doplňující geometrickou nebo statickou podmínku. Různé alternativy doplňkových podmínek jsou uvedeny v [2]. Jedním ze způsobu výpočtu je volba průvěsu křivky v jednom bodě vycházející z geometrických požadavků kladených na konstrukci (většinou se jedná o maximální průvěs zmax). Řešením náhradního nosníku je znám ohybový moment ve stejném bodě. Z těchto veličin lze následně stanovit vodorovnou sílu H a získat tak hodnotu jedné neznámé v rovnici a tedy i svislé pořadnice všech bodů průvěsové křivky lana.
SAMOKOTVENÝ SYSTÉM
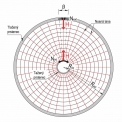
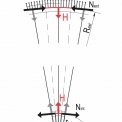
Konstrukce ve výchozím stavu při uvedeném podepření na ložiskách tvoří tzv. samokotvený systém. To znamená, že vodorovné složky kotevních sil z nosných lan H jsou zachyceny obvodovými prstenci. Konstrukce je v rovnováze, a pokud jsou povoleny vodorovné posuny, ohybově nenamáhá spodní stavbu. Ve výchozím stavu kotevní síly vyvozují ve vnějším prstenci tlakové a ve vnitřním prstenci tahové namáhání (obr. 7). V případě rovnoměrného zatížení vznikají v prstencích pouze normálové síly. Ohybové namáhání je minimální a je způsobeno radiálními účinky od osových sil v prstencích, které jsou dány mírou zakřivení prvku.
Vztah mezi jednotlivými parametry udává pro vnější prstenec následující rovnice: 
kde rext jsou radiální účinky na vnějším prstenci, Next je normálová síla ve vnějším prstenci, Rext je poloměr vnějšího prstence a lext je délka části vnějšího prstence mezi kotvením lan (obr. 8). Pro vnitřní prstenec platí stejná rovnice s příslušným indexováním.
Lze dokázat, že velikost normálových sil v obou prstencích se rovná, síly pouze mají opačné znaménko, tedy: ![]()
Po zmonolitnění již nedochází k výraznému nárůstu normálových sil v prstencích. Při vnesení předpětí prostřednictvím předpínacích lan se betonová membrána vlivem radiálních účinků lan nadzvedne a opře se o prstence. Tím svou tuhostí zachytává vodorovné složky sil z předpínacích lan a díky tomu je do ní vnesena tlakové napětí.
Vlivem normálových sil v prstencích dochází k jejich osovému stlačení (vnější prstenec) a roztažení (vnitřní prstenec). Díky tomu nejsou ve výchozím stavu svislé deformace nulové, jak bylo deklarováno. Díky vodorovným deformacím prstenců dochází k nárůstu svislých deformací konstrukce jako celku (obr. 9). Nulových deformací by bylo dosaženo pouze za předpokladu tuhých prstenců. Protože jsou však průřezy prstenců navrženy reálných velikostí a běžných materiálů, k jejich deformaci dochází, nejedná se však o chybu ve výpočtu.
DOTVAROVÁNÍ A SMRŠŤOVÁNÍ
Předpjatá membrána je tvořena lehkým konstrukčním betonem třídy LC40/50. Materiálové charakteristiky lehkého konstrukčního betonu lze získat pomocí charakteristik klasického betonu stejné třídy vynásobením příslušnými součiniteli η, které jsou definovány v příslušné normě, viz [3]. Do výpočtu těchto součinitelů vstupuje horní mez objemové hmotnosti po vysušení ρ pro příslušnou třídu. V případě navržené konstrukce byla zvolena třída objemové hmotnosti D1, 6, které odpovídá objemová hmotnost v rozmezí 1 401–1 600 kg/m3. Objemová hmotnost vyztuženého betonu se pak má uvažovat hodnotou 1 750 kg/m3. Pro porovnání jsou základní charakteristiky obyčejného a lehkého betonu stejné třídy uvedeny v tab. 1. Je patrné, že lehký beton má stejnou hodnotu pevnosti v tlaku jako obyčejný beton. Pevnost v tahu je cca o 14 % menší. Výrazný rozdíl je pak v modulu pružnosti a součiniteli dotvarování, jejichž hodnoty jsou v případě lehkého betonu téměř poloviční oproti obyčejnému betonu (obr. 10). Naopak smršťování vysycháním se má uvažovat hodnotou o 20 % větší (obr. 11). Velikost celkového smršťování lze ovlivnit řadou metod. V případě lehkých betonů je možné např. použít pórovité kamenivo vodou nasycené a tím značně snížit hodnoty autogenního smršťování.
Pro výpočet dotvarování a smršťování byly použity tyto vstupní parametry: třída cementu N, relativní vlhkost RH = 70 %, stáří betonu prefabrikovaných segmentů při osazení do konstrukce t0 = 60 dní, doba ošetřování sedm dní, náhradní rozměr průřezu h0 od 103 do 113 mm.
Vyhodnocení je zobrazeno na obr. 12. Vlivem smršťování a dotvarování dochází k svislým deformacím konstrukce směrem nahoru. Těmto deformacím pak odpovídá i nárůst ohybových momentů ve vetknutí do vnějšího prstence. Je patrné, že velký dopad na konstrukci má převážně smršťování. Po dokončení konstrukce (2. fáze výstavby) mají momenty velikost cca 32 kNm. Po jednom roku narostou na hodnotu 61 kNm a na konci životnosti, tedy ve 100 letech, se zvýší už pouze 5 kNm.
| Tab. 1 – Základní parametry obyčejného a lehkého betonu válcové pevnosti 40 MPa | |||
| C40/50 | LC40/50 | ρ = 1 600 kg/m3 | |
| fck = 40 MPa | flck = 40 MPa | ||
| fctm = 3,5 MPa | η1 = 0,4 + 0,6 · 1 600/2 200 = 0,836 | flctm = 0,836 · 6,2 = 2,9 MPa | |
| Ecm = 35,2 GPa | ηE = (1 600/2 200)2 = 0,529 | Elcm = 0,529 · 35,2 = 18,6 GPa | |
| φ(∞,t0) = 1,450 | (1 600/2 200)2 = 0,529 | φl(∞,t0) = 0,529 · 1,450 = 0,767 | |
| εcd,0 = 3,2E-4 | η3 = 1,2 | εlcd,0 = 1,2 · 3,2E-4 = 3,9E-4 | |
ZÁVĚR
Hlavním cílem analýzy předpjaté membrány ve tvaru mezikruží bylo pochopení statického působení a pojmenování základních principů spjatých s tímto typem konstrukcí. Získané poznatky mohou být dále využity na možnou aplikaci mezikruží jako zastřešení tribun hlediště fotbalového stadionu (obr. 13). Vzhledem k velikosti hrací plochy a přilehlých tribun by bylo nutné zvětšit nejen rozměry vnějšího prstence, ale rovněž odpovídajícím způsobem upravit průměr vnitřního prstence tak, aby byl zachován tradiční volný průzor na hrací plochu. Dále se nabízí rovněž možnost změnit kruhový půdorys na eliptický, který z hlediska zastavěné plochy více vyhovuje obdélníkovému tvaru fotbalového hřiště. Eliptická varianta zastřešení, vycházející z předpokladů formulovaných na základě analýzy předpjaté membrány ve tvaru mezikruží, byla řešena a publikována v rámci projektu Technologické agentury ČR, viz [4].
Článek vznikl za podpory projektu Technologické agentury České republiky TA02011322: „Prostorové konstrukce podepřené kabely a/nebo oblouky“.
LITERATURA:
[1] Stráský, J.: Visuté předpjaté střechy. Beton TKS, 2006, č. 1, s. 21–27.
[2] Kadlčák, J.: Statika nosných lan visutých střech. Praha, ACADEMIA, 1990.
[3] ČSN EN 1992-1-1 Eurokód 2: Navrhování betonových konstrukcí – Část 1-1: Obecná pravidla a pravidla pro pozemní stavby
[4] Juchelková, P., Stráský, J.: Předpjatá membrána nad eliptickým půdorysem jako zastřešení fotbalového stadionu. Beton TKS, 2013, č. 2.
An Analysis of a Prestressed Membrane with a Shape of Annulus
Article deals with static analysis of prestressed membrane in the shape of annulus. The membrane is made from ligth structural concrete. The notions of initial state or self-anchored system are explained. Finally, creep and shrinkage of ligth concrete are presented.