Výpočet dynamických sil v základech masivního padostroje při drop-in testech velkých těles

• Foto

PADOSTROJ - 3D MODEL PRO MKP
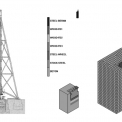
Pro řešení dynamického rázu (dopadu beranu) na zkušební těleso je nejvhodnější vytvořit model sítě konečných prvků a pak (po jeho řešení) provést analýzu reakčních sil v základech. Pro praktické výpočty (vysoký padostroj, viz obr. 3) byl zvolen program MSC. MARC/MENTAT, viz např. [1] až [4].

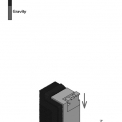
Na obr. 3 je vidět výkres celku a také model zkoumaného místa – síť konečných prvků (14 828 uzlů a 16 731 elementů), který byl vytvořený podle výkresové dokumentace. Model se skládá z několika částí. Ocelový beran (v obr. 3 značeno jako „STEEL-BERAN“) dopadá velkou rychlostí na ocelové zkušební těleso (značeno jako „STEEL-WHEEL“). Zkušební těleso je uloženo na ocelové kovadlině (značeno jako „STOCK-STEEL“), která je uložena na třech vrstvách dubových dřevěných trámů (značeno jako „WOOD‑FD1“, „WOOD‑FD2“ a „WOOD‑FD3“). Dřevěné vrstvy jsou uloženy na betonovém základu (značeno jako „BETON“). Veškeré materiály jsou považovány za elastické a izotropní (modul pružnosti, Poissonovo číslo a hustota). Při definici materiálu bylo také použito materiálové tlumení. Mezi beranem a zkušebním tělesem byl uvažován mechanický kontakt, který souvisí s dopadem beranu na zkušební těleso. Počáteční rychlost beranu je –5,695 m.s^–1 (čas t = 0 s, poznámka – z důvodů zkrácení výpočtu je zvolena počáteční poloha beranu již cca v 1/3 své dráhy) ve zvolené výšce 10,599 m (měřeno i se statickým zatížením základů, které je v místě dopadu 2,697 mm). Beran se po uvolnění pohybuje rovnoměrně zrychleným pohybem vlivem vlastní tíhy směrem ke zkušebnímu tělesu. Zkoumaný čas lze tedy rozdělit na dobu před prvním dopadem beranu t d (0 ; 1) s a na dobu po prvním dopadu beranu t Є (1 ; 5) s. Na soustavu také působí gravitační síly (tíhové zrychlení g = 9,807 ms^–2) a také pružný Winklerův podklad, který nahrazuje jednoduchým způsobem poměrně komplikované vlastnosti jílového podloží (modul podloží K = 2,5 × 10⁷ Nm^–3), viz obr. 4. Pružný podklad tedy obklopuje betonový základ ze spodu a z boku. Při řešení této nelineární úlohy byla nastavena proměnlivá délka kroku v implicitním řešiči software MSC.MARC. Nutno podotknout, že program MSC. MARC umožňuje také použití explicitního řešiče. Vlivem rázu beranu do zkušebního tělesa vznikne v základech padostroje kmitání, které se následně utlumí vlivem materiálového tlumení.

PADOSTROJ - VÝSLEDKY VÝPOČTU POMOCÍ MKP
Beran se až do okamžiku dopadu pohybuje rovnoměrně zrychleným pohybem (proti směru souřadnicové osy Z). Průběhy rychlostí v časech t = 0 s (0. krok, počátek řešení), t = 0,5 s a t = 1 s (dopad beranu na zkušební těleso) je znázorněn na obr. 5. Vypočtená dopadová rychlost beranu na kovadlinu je –15,502 m.s^–1 (čas t = 1 s). Obrázky 6 znázorňují průběhy rychlostí v časech t = 1,00101 s (60. krok řešení), t = 1,26748 s (144. krok řešení) a t = 3,65352 s (165. krok řešení). Z uvedeného je také zřejmé, že se beran po odrazu pohybuje směrem nahoru (proti směru souřadné osy Z) a po dosažení horní úvrati, se opět pohybuje směrem dolů a naráží podruhé na zkušební těleso. Druhý ráz již není tak významný, protože jeho rázová energie je menší než při prvním rázu.

Nutno podotknout, že v obecném případě je velikost odrazu silně ovlivněna nejen tlumícími účinky a pasivními odpory ve vedení beranu, ale především také způsobem uchycení zkušebního tělesa a hlavně materiálovými vlastnostmi zkušebního tělesa a beranu (např. křehké těleso, vlivem křehkého lomu, tj. expandování trhlin, odvádí větší množství pádové energie a dráha po odrazu beranu je pak menší nebo dokonce nulová).

Na obr. 7 jsou znázorněny ve čtyřech pohledech výsledné průhyby [m] v základové části padostroje těsně před dopadem beranu (t = 1 s), které jsou vyvolené statickým zatížením od vlastní tíhy a také uložením na pružném podkladu. Maximální hodnota tohoto průhybu je Δ_{MAX t=1} = 2,780 mm.

Na obr. 8 jsou znázorněny ve čtyřech pohledech výsledné průhyby ve spodní části padostroje v čase po dopadu beranu (dynamické zatížení 54. krok výpočtu, t = 1,00055 s). Maximální hodnota tohoto průhybu je Δ_{MAX t=1,00055} = 6,082 mm. Na obr. 9 jsou znázorněny ve čtyřech pohledech výsledné průhyby v základové části padostroje v čase po dopadu beranu (dynamické zatížení 91. krok výpočtu, t = 1,02685 s). Maximální hodnota tohoto průhybu je Δ_{MAX t=1,02685} = 9,050 mm. Právě hodnota Δ_{MAX t=1,02685} je největší výsledný průhyb základů v celém intervalu řešení.

Pro dynamický koeficient výsledných průhybů základů stroje (tj. poměr maximálního výsledného průhybu vyvoleného rázem a maximálního průhybu od statického předpětí) platí:

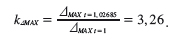
Pro další potřeby je třeba provést rozbor průhybů w [m] ve směru osy Z a to na spodní části betonových základů padostroje (potřebné pro zjištění reakčních sil v podloží). Pro tuto analýzu je vhodné si zvolit několik charakteristických uzlů sítě konečných prvků. Závislost průhybu w na čase t je pro tyto uzly znázorněná v [1] a [2]. Od statické hodnoty jsou v intervalu t Є (1 ; 5) s zřejmé dvě dynamické změny vyvolané prvním a druhým dopadem beranu. Z průběhů těchto závislostí je zřejmé, že průhyb pod betonovým základem je prakticky totožný po celé ploše spodní části styku betonových základů s jílovou půdou. Proto se nabízí praktické zprůměrování těchto hodnot, které je zatíženo vzhledem k přijatým zjednodušením jen malou chybou. Zprůměrování těchto hodnot (referenční hodnoty průhybů) již pro interval t Є (1 ; 5) s je znázorněno na obr. 10.

Z uvedeného je zřejmé (obr. 10), že pro deformační zatížení základů padostroje od vlastní tíhy (statické předpětí, tj. stlačení ve směru osy Z) lze stanovit referenční hodnotu w_STAT = –2,651 mm (čas t = 1 s). Dynamické chování spodní části základů padostroje, po dopadu beranu na zkušební těleso, lze charakterizovat jeho referenčními špičkami w^-_DYN = –8,967 mm (čas t = 1,02685 s) a w⁺_DYN = 3,655 mm (t = 1,07785 s), viz obr. 10. Pro dynamický koeficient průhybů w spodní části základů padostroje (tj. poměr největšího referenčního průhybu (myšleno v absolutní hodnotě) vyvoleného rázem a maximálního průhybu od statického předpětí) platí:

Obdobným postupem lze také stanovit výslednou referenční hodnotu síly F_R = p_RA = KwA [N], která působí ve směru souřadnicové osy Z a která se přenáší ze spodní části základů padostroje do jílové půdy, kde p_R = Kw [Pa] je tlak v podkladu dle Winklera a A [m²] je plocha spodní části styku základů padostroje s jílovou půdou. Závislost síly F_R v čase t d (1 ; 5) s je znázorněná na obr. 11.

Z uvedeného je zřejmé (obr. 11), že pro silové zatížení základů padostroje od vlastní tíhy (statické předpětí, tj. referenční výsledná reakční síla ve směru osy Z) lze stanovit referenční hodnotu FR_STAT = -755 479 N (čas t = 1 s). Dynamické chování spodní části základů padostroje, po dopadu beranu na zkušební těleso, lze charakterizovat jeho referenčními špičkami sil F^-R_DYN = -2 555 721 N (čas t = 1,02685 s) a F⁺R_DYN = 1 041 657 N (čas t = 1,07785 s),viz obr. 11. Pro dynamický koeficient reakčních sil FR spodní části základů padostroje (tj. poměr největší referenční síly (myšleno v absolutní hodnotě) vyvolené rázem a maximální referenční síly od statického předpětí) platí:

ZÁVĚR
Uvedeným postupem byly pomocí MKP stanoveny reakční síly v podloží nově projektovaného masivního padostroje znázorněného na obr. 3, což dává důležitou informaci pro konstruktéry (zadavatelskou firmu).

Článek vznikl v rámci projektu CZ.1.05/2.1.00/03.0069 „ENET – Energy Units for Utilization of non Traditional Energy Sources“ (ENET – Energetické jednotky pro využití netradičních zdrojů energie).

LITERATURA:
[1] Frydrýšek, K., Nikodým, M.: Beams and Frames on Elastic Foundation 3 (Nosníky a rámy na pružném podkladu 3), ISBN 978-80-248-2257-0, VŠB – Technical University of Ostrava, Ostrava, Czech Republic, 2010, pp. 611
[2] Frydrýšek, K., Fries, J.: Aplikace konstrukcí na pružném podkladu, ISBN 978-80-248-2361-4, VŠB - Technical University of Ostrava, Ostrava, Czech Republic, pp. 204
[3] Frydrýšek, K.: Praktikum software MSC.MARC/MENTAT – část 1 (Practicum of MSC.MARC/MENTAT Software – Part 1), Faculty of Mechanical Engineering, VŠB-Technical University of Ostrava, ISBN 978-80-248-2125-2, Ostrava, Czech Republic, 2009, pp. 154
[4] Frydrýšek, K., Fusek, M., Hrabec, J.: Praktikum software MSC. MARC/MENTAT – část 2, Faculty of Mechanical Engineering, VŠB – Technical University of Ostrava, Ostrava, ISBN 978-80-248-2211-2, Ostrava, 2010, Czech Republic, pp. 144

Calculation of Dynamic Forces in the Foundations of a Massive Drop-Tester During the Drop-In Testing of Big Bodies
In technical practice, seen e.g. in Fig. 1 and 2, drop tests of parts or machinery units are often required. In test rooms there is really modern equipment for high-speed collision tests with demanding opto-electronics and electronics. In our country and abroad there are many types of drop testers for various drop heights (about hundred meters) various weights (tenths of tons) and various drop energies (more than 106 J), see [1], [2]. In the article reaction forces were set using mentioned procedure by the means of MKP in subsoil of newly projected massive drop tester shown in Fig. 3, which provides important information for constructers. (Contracting company).

Autor

• Doc. Ing. Frydrýsek Karel Ph.D.