Vyhodnocení porušení a plasticity betonu u rovinných úloh

K vyhodnocování stavu porušení, případně plasticity betonu u rovinných úloh nestačí pouze pracovní diagram pro jednoosý stav napjatosti. Problém se řeší formulováním dvojrozměrné podmínky porušení a plasticity. Podmínky betonu musí respektovat odlišné chování betonu při namáhání tlakem a tahem. Pro uvedený problém bylo postupně formulováno několik podmínek, které jsou definovány pro dva a více parametrů [8, 9]. Pro pružnoplastické konstitutivní modely betonu jsou nejznámější podmínky, které navrhl Chen [1] a Willam a Warnke [16]. K vyhodnocení dosažení meze porušení betonu je zase rozšířená Kupferova podmínka [5] nebo modifikovaná podmínka von Mises. Další možností je použití doporučení dle CEB‑FIB Model Code 90 [3].

Příspěvek se zabývá blíže srovnáním Chen-Chenovy podmínky [2] a doporučením dle CEB-FIB Model Code 90 [3]. Pro ukázku je při grafickém vyhodnocení podmínek v rovinně hlavních napětí uvedena také modifikovaná podmínka von Mises pro beton.

PODMÍNKA PORUŠENÍ DEFINOVANÁ CEB-FIB
Vhodnou možností vyhodnocení stavu betonu u rovinných úloh je použití doporučení uvedeného v CEB-FIB Model Code 90 [3]. Podmínka vznikla na základě experimentů. Parametry podmínky CEB‑FIB Model Code 90 jsou jednoosá pevnost betonu v tlaku f_uc a v tahu f_ut. Hodnota dvouosé pevnosti betonu v tlaku se uvažuje 1,2 f_uc. Pro formulování a vyhodnocení podmínky se vychází z předpokladu, že platí σ1 > σ2. Pomocný součinitel se vypočte α = σ1 / σ2. Vymezení podmínky CEB-FIB Model Code 90 pro oblasti definované v intervalu σ2 jsou:

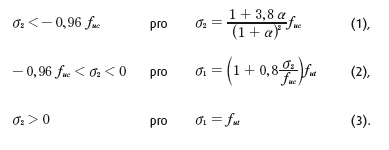
CHEN-CHENOVA PODMÍNKA
Pro pružnoplastické konstitutivní modely betonu je vhodná například podmínka, kterou navrhl Chen [2]. Chen-Chenova podmínka porušení a plasticity byla formulována na základě experimentů provedených Kupferem [5]. V oblasti tlak – tlak je podmínka plasticity popsána funkcí:



Podmínka je tedy definována pomocí mezí plasticity materiálu v jednoosém tlaku f_yc, mezí plasticity ve dvojosém tlaku f_ybc a mezí plasticity v jednoosém tahu f_yt. V numerické studii srovnávající podmínky porušení jsou za parametry v Chen-Chenově podmínce použity pevnosti betonu místo mezí plasticity betonu.

MODIFIKOVANÁ PODMÍNKA VON MISES PRO BETON
Uvedená podmínka porušení betonu modifikuje kritérium von Mises [13] a [10].

Má tvar:



Podmínka porušení je pro namáhání tah-tah omezena pevností betonu v tahu. Pro kombinaci tah-tlak je nutné uplatnit při vyhodnocování podmínky obě pevnosti.

SROVNÁNÍ PODMÍNEK
Numerická studie srovnává v rovině hlavních napětí podmínky porušení pro vybraný model betonu, který má v jednoosém tlaku pevnost 20 MPa. Srovnány jsou Chen-Chenova podmínka, doporučení dle CEB-FIB Model Code 90 a modifikovaná podmínka von Mises pro beton.

Pevnost betonu v jednoosém tahu se určila pro studii [14]:



Modul pružnosti betonu je 30 GPa a Poissonův součinitel 0,2. Grafické vyhodnocení zvolených podmínek porušení v rovině hlavních napětí je zobrazeno na obr. 1.

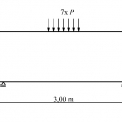
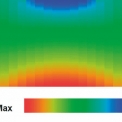
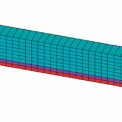
Druhou částí numerické studie je srovnání Chen-Chenovy podmínky pro porušení [1] a doporučení dle CEB-FIB Model Code 90 [3] u výpočetního modelu, který tvoří vysoký nosník. Zatížení tvoří sedm bodových sil na horním okraji. Rozměry vysokého nosníku jsou 3 m × 1 m. Poloha zatížení a okrajových podmínek jsou patrné z výpočetního modelu na obr. 2. Délka uložení je 0,3 m a tloušťka konstrukce je 0,2 m. Výpočetní model tvoří pravidelná síť izoparametrických konečných prvků se čtyřmi integračními body, ve kterých se vyhodnocovaly podmínky pro beton. Výpočetní model tvoří 900 konečných prvků ve tvaru obdélníků. Průběh normálových napětí je zobrazen na obr. 3.

Grafické vyhodnocení podmínek u vysokého nosníku je znázorněno na obr. 5.

PRUŽNOPLASTICKÝ MODEL BETONU
Dále je uvedená studie parametrů počáteční podmínky plasticity. Zvolený pružnoplastický model betonu kombinuje Chen-Chenovu podmínku plasticity [1] a model zpevnění vypracovaný Ohtanim [7]. Uvedený konstitutivní model betonu je implementován v software BSA vyvíjeném na VŠB-TU Ostrava [14, 15]. Chen-Chenova podmínka plasticity [1] je definována pomocí mezí plasticity materiálu. Pro použití konstitutivního modelu betonu je také nutné definovat podmínku porušení, která se získá z pevnosti betonu v jednoosém tlaku f_uc, pevnosti betonu v dvojosém tlaku f_ubc a pevností betonu v jednoosém tahu f_ut. Mez plasticity materiálu je možné následně vyjádřit pomocí koeficientu a pro jednotlivé způsoby namáhání jako:

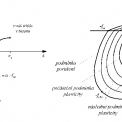
Hodnoty koeficientu a se nejčastěji volí od 0,3 [2] až 0,5 [13]. Parametrická studie je provedena pro pět vybraných hodnot koeficientu α. Počáteční plocha plasticity, následné plochy plasticity a plocha porušení jsou zobrazeny v rovině hlavních napětí na obr. 6. Na obrázku je také znázorněn pracovní diagram betonu.

STUDIE PRO PARAMETRY POČÁTEČNÍ PODMÍNKY PLASTICITY
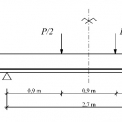
Modelovaným experimentem zvoleným pro studii parametrů počáteční podmínky plasticity je železobetonový nosník, který je zatížený dvěma silami. Zvolený experiment provedli a publikovali Gaston, Siess a Newmark [4]. Podklady z provedeného experimentu jsou převzaty z publikace [6]. Schéma experimentu je zobrazeno na obr. 7.

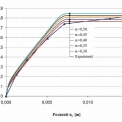
Nosník je z betonu o pevnosti v tlaku 32,3 MPa. Modul pružnosti betonu E_c je 27,1 GPa a Poissonův součinitel 0,17. Výpočet je proveden postupně pro koeficient α s hodnotou 0,3, 0,35, 0,4, 0,45 a 0,5, který se použil k výpočtu parametrů (10), (11), (12) počáteční podmínky plasticity. Stupeň vyztužení ρ železobetonového průřezu vztažený k efektivní výšce průřezu je 0,0062. Pracovní diagram výztuže se předpokládá ideálně pružnoplastický. Mez kluzu oceli f_y je 323,6 MPa a modul pružnosti E_s je 198,0 GPa. Rovinný výpočetní model [11] je prezentován na obr. 8. Pro názornost je vizualizace výpočetního modelu provedena prostorově v preprocesoru výpočetního systému ANSYS [12].

Porovnáním experimentu a výsledků numerických výpočtů je možné konstatovat, že ve většině výpočtů je mírně nadhodnocena počáteční tuhost výpočetního modelu. Pouze u výpočtu pro α = 0,30 je tuhost výpočetního modelu mírně podhodnocená. Dále je při zatěžování rozdíl pracovních diagramů numerických výpočtů a experimentu malý. Celkový průběh pracovního diagramu experimentu a maximální únosnost nosníku nejlépe vystihuje výpočet pro α = 0,45. Dobrou shodu celkového průběhu pracovního diagramu experimentu má také výpočet pro α = 0,40.

ZÁVĚR
Uvedené podmínky mohou být využity při návrhu konstrukcí pro ověřování mezního stavu použitelnosti a analýz konstrukčních detailů, kde je nutné ověřit vznik trhlin betonu. Z grafického porovnání podmínek porušení pro beton v rovině hlavních napětí vyplývá, že modifikovaná podmínka von Mises podhodnocuje pevnost betonu v tlaku a oblasti namáhané tahem  nadhodnocuje. Podmínka definovaná CEB-FIB Model Code 90 respektuje vlastnosti betonu v tlaku a tahu. Podmínka je definována pouze pro dva vstupní parametry. Chenova podmínka také dobře vystihuje chování betonu, kdy je nezbytné určit tři vstupní parametry. Třetí parametr je pevnost betonu v dvouosém tlaku. Chenova podmínka ve srovnání s ostatními podmínkami podhodnocuje pevnost betonu v tahu. U příkladu vysokého nosníku byla oblast porušení pro Chenovu podmínku a podmínku dle doporučení CEB-FIB podobná. Rozdíl porušení betonu v integračních bodech činil u zvolených podmínek 0,22 %.

Příspěvek se dále zabýval volbou parametrů počáteční podmínky plasticity u pružnoplastické analýzy železobetonových konstrukcí. Z provedené parametrické studie pro pět hodnot koeficientu α byl pro zvolený experiment nejvhodnější α = 0,45.

Projekt byl realizován za finanční podpory ze státních prostředků České republiky prostřednictvím Studentské grantové soutěže v rámci specifického výzkumu na Vysoké škole báňské – Technické univerzitě Ostrava. Registrační číslo projektu je SP2012/94.

LITERATURA:
[1] Chen, A. C. T., Chen, W. F. Constitutive Relations for Concrete. Journal of the Engineering Mechanics Division ASCE, 1975
[2] Chen, W. F. Plasticity in Reinforced Concrete. Mc. New York: Graw Hill, 1982
[3] CEB‑FIP Model Code 1990: Design Code. by Comite Euro-International du Beton, Thomas Telford, 1993. ISBN: 978-0727716965
[4] Gaston JR, Siess CP, Newmark NM. A layered finite element non-linear analysis of reinforced concrete plates and shells. Civil Engineering Studies, SRS No. 389, Univ. of Illinois, Urbana, 1972
[5] Kupfer H., Hilsdorf H.,K., Rüsch H. Behaviour of Concrete Under Biaxial Stress, Journal ACI, Proc. V. 66, č. 8, 1969
[6] Kwak, HG, Kim, SP, Bond-slip behavior under monotonic uniaxial loads, Journal Engineering structures, Vol. 23, Iss.: 3, pp. 298–309, 2001. ISSN 0141-0296
[7] Ohtani, Y., Chen, W. F.: Multiple Hardening Plasticity for Concrete Materials. Journal of the EDM ASCE,1988
[8] Programový systém ATENA 2D: Theory Manual. Praha: Červenka Consulting, 2000
[9] PROCHÁZKA, J. a kol.: Navrhování betonových konstrukcí 1. 2. vyd. Praha: ČVUT v Praze, 2006. ISBN 80-903807-1-9
[10] Ravinger, J. Programy – statika, stabilita a dynamika stavebných konštrukcií. Alfa, Bratislava, 1990
[11] Rombach, G.: Anwendung der Finite-Elemente-Methode im Betonbau. 2. Auflage. Berlin: Ernst & Sohn, 2007, ISBN 978-3-433-01701-2.
[12] RELEASE 11 DOCUMENTATION FOR ANSYS, SAS IP, INC., 2007
[13] Servít, R. a kol.: Teorie pružnosti a plasticity II, Praha: SNTL/ALFA, 1984. ISBN 978-80-7318-440-7
[14] Sucharda, O., Brožovský, J.: Pružnoplastické modelování železobetonového nosníku: implementace a srovnání s experimentem. Sborník vědeckých prací VŠB-TUO, řada stavební. 2011, roč. 11, č. 1, s. 237–244. ISSN: 1213-1962
[15] Sucharda, O., Brožovský, J. Modely betonářské výztuže pro konečněprvkovou analýzu konstrukcí. Sborník vědeckých prací VŠB-TUO, řada stavební, 2011, roč. 11, č. 2, s. 249–258. ISSN 1213-1962
[16] Willam, K., J., Warnke, E., P.: Constitutive Model for the Triaxial Behavior of Concrete, Proceedings of International Association for Bridge and Structural Engineering, Bergamo, 1975

Comparison of failure and plasticity conditions for concrete in plane problems
The paper deals with a comparison of selected failure and plasticity conditions of concrete. The article includes the study carried out for parameters of initial plasticity conditions. The selected conditions of failure are compared in 2D and two of them are used by the analysis of high beam. The reinforced concrete beam loaded by two forces is chosen for study of parameters of initial plasticity condition. The used constitutive model of concrete for the nonlinear analysis combines Chen-Chen plasticity condition with Ohtani hardening model.

Autoři

• Ing. Sucharda Oldřich
• Doc. Ing. Brožovský Jiří Ph.D.