Teoretické a konštrukčné problémy novodobých ľahkých sústav z ocele, lán a membrán

Pri vytváraní týchto sústav pracujeme zväčša s materiálmi ako je oceľ, zliatiny hliníka a kompozitné materiály. Vytvárame tak rôzne sústavy z ocele, lán a membrán (obr. 1). Návrh každej takejto sústavy prináša so sebou aj nové teoretické a konštrukčné problémy. Bez ich vyriešenia nie je možné napredovať a ich riešenie veľa krát nie je jednoduché.

Obr. 1 – Ľahká sústava z ocele lán a membrán

PROBLÉMY NOVODOBÝCH SÚSTAV
Hovoriť o novodobých sústavách z ocele, lán a membrán má svoje opodstatnenie. A to, že práve tieto sústavy stoja na vrchole súčasných staviteľských možností. Limity sú dané fyzikálnymi vlastnosťami a zákonmi materiálu a konštrukčného systému. Tieto je pri tvorbe novodobej sústavy potrebné dokonale zohľadňovať a využívať. V praxi sa najčastejšie stretávame s riešením týchto problémov:

• prútové sústavy – stabilitné problémy tlačených a ohýbaných prútov,
• lanové sústavy – predpätie, tuhosť konštrukcie, nutnosť riešenia teóriou II. Rádu,
• membránové sústavy – predpätie, dynamická odolnosť, riešenia s použitím veľkých deformácii.

MEMBRÁNY
Membránové konštrukcie, sú veľa krát označované za textilné konštrukcie (stany). Skutočná membránová konštrukcia je však klasickému stanu značne vzdialená. Hlavným rozdielom je jej presný geometrický tvar. Pre fungovanie membránovej konštrukcie musia byť dodržané výpočtom presne stanovené geometrické kritéria. Základným kritériom je dodržanie výmeny konkávnosti a konvexnosti hlavných smerov plochy membrány. Po dodržaní tohto princípu môžeme hovoriť o základných štyroch typoch membrán (obr. 2):

• sedlový tvar (hyperbolický paraboloid),
• kužeľový tvar,
• tvar vlny,
• klenbový tvar.

Ďalším kritériom ľahkej membránovej konštrukcie je jej predpätie. Správny geometrický tvar a predpätie zaručuje jej stabilitu, tuhosť a dynamickú odolnosť. Zároveň umožňuje konštrukcii odolávať vplyvom na ktoré bola navrhnutá, napr. dažďu, vetru a snehu.

GEOMETRICKÝ TVAR MEMBRÁN
Základný geometrický tvar membránovej sústavy vychádza z plochy hyperbolického paraboloidu (obr. 3).

Túto plochu dokážeme matematicky popísať vzťahom [3]:

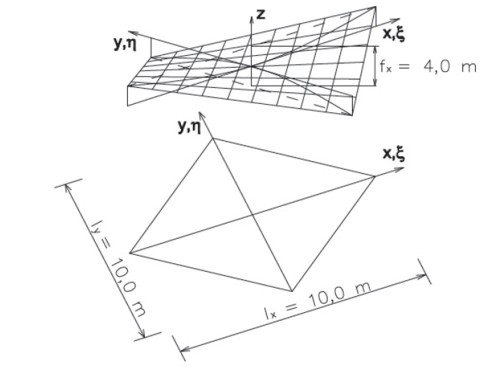
Pre plochu s paralelnými okrajmi zakrivenia a pravouhlým pôdorysom môžeme zadefinovať nasledujúce rozmery plochy l_x, l_y, f_x, a f_y (obr. 4). Z okrajových podmienok:



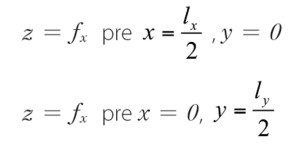
potom vyplývajú koeficienty:


po dosadení dostaneme:

Vyjadríme si dĺžkové súradnice, ktoré potom budú:



Po zjednodušení výrazu (3) dostaneme:


MATERIÁLOVÉ VYHOTOVENIE MEMBRÁN
Novodobé membránové sústavy sú vyrábané z rôznych typov textilných membrán. Tieto sú vyrábané ako kompozitné materiály a takmer vždy sú tvorené nosným tkaným jadrom a povrchovým filmom (obr. 5). Nosné jadro má nosnú funkciu a teda prenáša silové zaťaženie na membránu. Povrchový film ma ochrannú funkciu, zabezpečuje nepremokavosť a nepriedušnosť membrány.

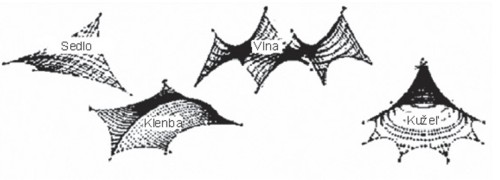
Obr. 2 – Základne typy membránových konštrukcii

Textilné membrány používane v stavebníctve môžeme podľa chemického zloženia rozdeliť do niekoľkých skupín:

PTFE (Polytetrafluoroethylene)
Teflon je syntetický fluoropolymer, má veľmi široké uplatnenie v priemysle a stavebníctve. Má vysokú odolnosť voči chemickým látkam a extrémne nízky koeficient trenia. Za najznámejší membránový materiál z PTFE sa dá považovať Gore-Tex. Najväčšou konštrukciou z PTFE môžeme označiť strechu „Hubert H. Humphrey Metrodómu“ v Mineapolise s plochou cca 80 000 m2, kde je použitá dvojvrstvová membrána s nosnou konštrukciu so sklených vláken. Pevnosť PTFE membrán v ťahu je 2 300–4 500 N/5 cm. V prípade, že ako nosný materiál budú použité sklenené vlákna, pevnosť v ťahu takejto membrány bude 3 500–7 500 N/5 cm.

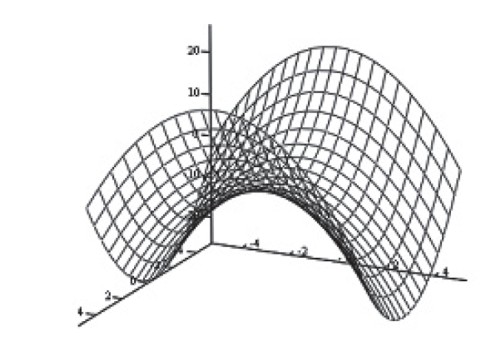
Obr. 3 – Všeobecná plocha hyperbolického paraboloidu

ETFE (Ethylene Tetrafluoroethylene)
ETFE je fluorocarbon – základný polymér (fluoropolymér) druh plastu. Bol navrhnutý ako materiál s vysokou odolnosťou proti korózii a odolnosťou v širokom rozsahu teplôt. Bol použitý napr. pre pneumatické panely plášťa futbalového štadiónu „Allianz Arény“, alebo v Pekingu na „Národné centrum vodných športov“ – najväčšia konštrukcia na svete zhotovená z ETFE membrány. Tiež na panely „Tropického Ostrova“ 20 000 m2 v Nemecku. ETFE sa bežne používa v nukleárnom priemysle pre priečky alebo lanovú bandáž. Pretože ETFE má výbornú mechanickú tuhosť a chemickú odolnosť, s ktorou môže súperiť s polytetrafluóretylénom (PTFE). Navyše má ETFE vysoký – energetický radiačný odpor a môže znášať mierne vysoké teploty pre dlhé časové obdobie. Komerčné označenie ETFE sú Tefzel od Du- Pont, Fluon od Asahi Glass a Texlon od Foiltec. Pevnosť ETFE membrán v ťahu je cca 1 200 N/5 cm a ETFE fólií 430–500 N/5 cm.

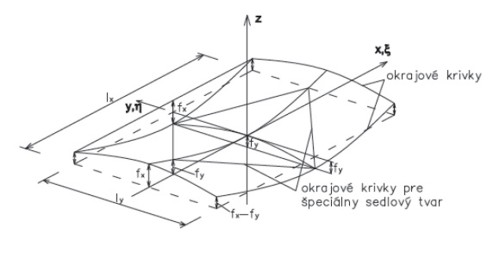
Obr. 4 – Hyperbolický paroboloid s paralelnými okrajmi zakrivenia


Obr. 5 – Skladba materiálu membrány

PVC (Polyvinylchlorid)
PVC je menej pevný a viac deformovateľný materiál, ale zároveň odolnejší voči mechanickým deformáciám. Má nižšiu životnosť v porovnaní z PTFE materiálom. Nosným materiálom u týchto membrán je polyesterové, alebo aramidové vlákno. Výhodou je najnižšia cena zo všetkých používaných materiálov a nižšia horľavosť. Pevnosť PVC membrán v ťahu v kombinácií s polyesterovým nosným vláknom je 3 000–9 800 N/5 cm a s aramidovým nosným vláknom 7 000–24 500 N/5 cm.

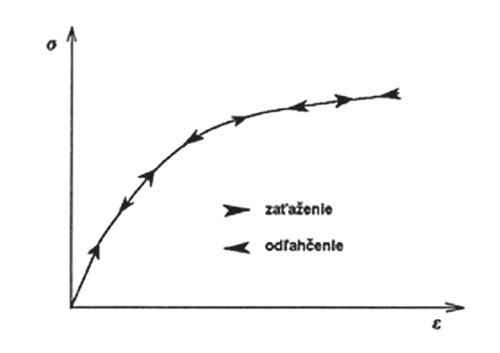
Obr. 6 – Hyperelastické zaťaženia a odľahčenie

Silikon
Silikón je veľmi progresívny materiál, používa sa v kombinácii s nosnou konštrukciou so sklených vláken. Má vysokú životnosť nad 30 rokov, tretinovú cenu PTFE materiálu a ako u jediného z používaných materiálov nie je jeho dym toxický. Silikón sa používa prevažne v kombinácií so sklenenými nosnými vláknami a pevnosť v ťahu takejto membrány je 3 500–6 000 N/5 cm.

Obr. 7 – Geometria riešenej plochy membrány

MATERIÁLOVÉ MODELY PRE MODELOVANIE MEMBRÁN
Materiálové, alebo pracovné modely membrán, sú prenesením reálneho správania sa materiálu a aproximačného pohľadu na ich modelovanie. Vzhľadom na šírku škály používaných materiálov a ich prevedenia, sa aj spôsoby ich modelovanie líšia. Najjednoduchší spôsob je interpretovať materiál membrány ako zidealizo-vaný izotropný materiál, s konštantným modulom pružnosti a Poisonnovou konštantou. Táto interpelácia má svoje výrazne nedostatky hlavne vzhľadom na štruktúru textílii. Za presnejší model možno považovať anizotropne ortogonálny – ortotropný materiálový
model. Týmto sme schopný zachytiť vzdialenosť vlastností materiálu v dvoch na seba kolmých smeroch. Ortogonalita materiálu vzniká ako nutná imperfekcia pri výrobe – tkaní, nosného jadra.

Obr. 8 – Diskretizovaný model membrány

• Izoparametrický model
• Anizotropne ortogonálny (ortotropný)
• Hyperelastický material (Neo-Hook, Mooney-Rivlin, Ogden)
• Viscoelastický material (Maxwell)

HYPERELASTICKÝ MATERIÁLOVÝ MODEL
Hyperelasticita je jav keď sa teleso po deformácií vracia do pôvodného stavu [2]. Závislosť medzi napätím a pomerným pretvorením sa dá popísať nelineárnou krivkou (obr. 6). Zaťaženie aj odľahčenie prebieha po tej istej krivke. Konštitutívne modely pre takéto materiály sú odvodené z potenciálu deformačnej energie pričom sa vychádza z predpokladu izotropnej deformácie. Ďalej treba brať do úvahy že hyperelastické materiály sú takmer nestlačiteľné teda ich Poissonová konštanta o = 0,5. Typickým príkladom hyperelastického materiálu je guma. Je ním možne modelovať tiež takmer všetky polyméry uhlíka, sklené vlákna a v neposlednom rade aj biomateriál (cievy, svaly).
Najčastejšie používane konštitutívne materiálové modely sú:

• Neo-Hookov model,
• Mooney-Rivlinov model,
• Ogdenov model.

Napätie u hyperelastického materiálu je funkcia deformačnej energie, čo môžeme symbolicky vyjadriť ako (5):

Deformačnú energiu je možno vyjadriť funkciou invariantov Cauchy-Greenovho napätia:


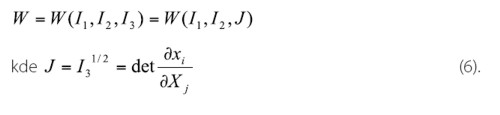
Invarianty redukovaných napätí sú:



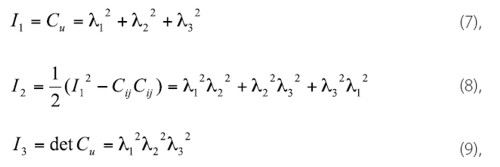
kde  sú hodnotý hlavných pretvorení a Cij sú komponenty Cauchy-Greenovho tenzora. Pre hlavné pretvorenia platí (10):



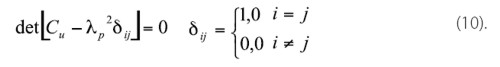
Redukované tvary invariantov budú vyzerať nasledovne:


Mooney-Rivlinov model je jeden z najpoužívanejších modelov, je vhodný pre takmer nestlačiteľný materiál, akým je napr. guma. Môže byť vyjadrený ako 2, 3, 5, 9-parametrický model.



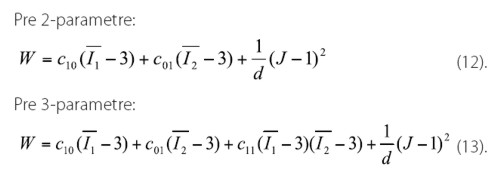
Mooney-Rivlinové materilové parametre c10, c01, c11,… môžeme vyjadriť prostredníctvom Cauchyho napätia (14):


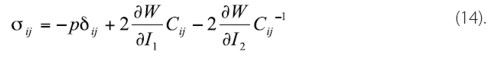
A následnou implementáciou metódy najmenších štvorcov:

MODELOVANIE A VÝPOČET
Pre modelovanie ilustračného príkladu jednoduchej membránovej plochy bol použitý program ANSYS. Membránová plochy bola namodelovaná v tvare hyperbolického paraboloidu (obr. 7). Pôdorysne rozmery tejto plochy sú 10,0 × 10,0 m. Dva protiľahlé rohy pôdorysu od pôvodnej roviny prevýšené o 4,0 m. Spojnice určujúcich bodov sú následne preložené rovinou s minimálnou plochou, čím vznikne už spomínaná plocha heperboloidu. Hrúbka membránovej plochy je 1 mm.

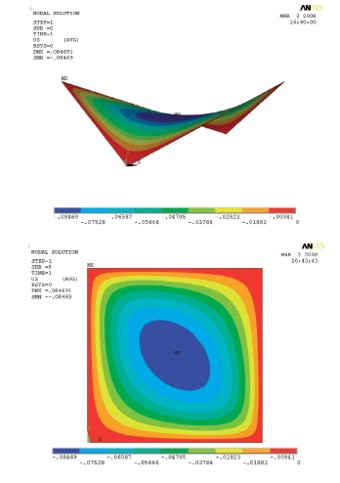
Obr. 9 – Deformácia v smere z

Diskretizácia plochy bola vykonaná pomocou plošného elementu Shell 181 (obr. 8). U tohto elementu je možne voliť medzimembránovým a doskovým stavom, dokáže pracovať s veľkými deformáciami a je možne použiť hyperelastický materiál. Pre základný prípad bol použitý izotropný materiál s modulom pružnosti E = 1 000 MPa a Poissonovou konštantou o = 0,3. Okrajové podmienky sú definovane ako kĺbové uloženie po obvode plochy. Do membránovej plochy bolo následne vnesené predpätie 330 kN, ktoré vylúčilo tlakové sily. Membrána je ďalej zaťažené plošným zaťažením 1 kN/m², ktoré predstavuje približne zaťaženie snehom.

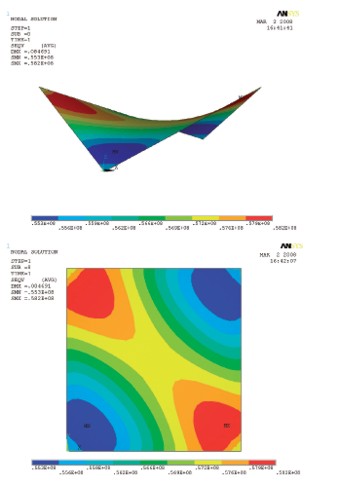
Obr. 10 – Von Mises napätie

Bol prevedený nelinárny výpočet s použitím plnej Newton Raphsonovej iterácie a s pripustením veľkých deformácii. Následne sme dospeli k výslednej membránovej sile 60,90 kN/m´ (3 045 N/5 cm) (obr. 9) a vertikálnej deformácii v strede rozpätia –84,7 mm (obr. 10). Z čoho možno konštatovať, že ide o pomerne veľkú deformáciu a napätie od predpätia bude niekoľko násobne vyššie ako napätie vyvolané plošným zaťažením.

ZÁVER
Modelovanie a analýza membránových konštrukcií pomocou programu ANSYS je pomerne náročná záležitosť, najmä dokiaľ pri ňom dochádza ku kombinácií viacerých typov elementov, napríklad plošného s prútovým. Pre návrh reálnej konštrukcie ma význam len model ktorý bude zohľadňovať reálny stav. V súčasnosti pracujem na doladení modelu v ktorom bude predpätie do membrány vnášane prostredníctvom lán a plošné zaťaženie bude vnášané do plochy membrány ako reakcia vznikajúca prúdením vzduchu.

Autoři

• Ing. Vaník Peter
• Prof. Ing. Dr. Agócs Zoltán Ph.D.