Stanovení tlaků ve styku mobilní výztuže s počvou

• Foto

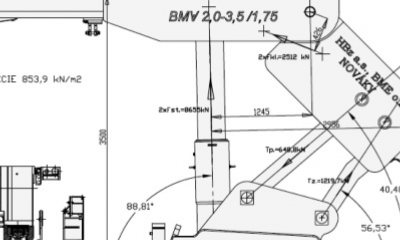
Bylo zadáno provedení výpočtu rozložení tlaků ve styku spodní části výztuže s počvou a to pro šest variant polohy při různých pojistných tlacích, viz např. obr. 2.

Pro řešení byla využita metoda konečných prvků (software MSC.MARC/MENTAT 2008 r1). Vzhledem k neurčitým vlastnostem podloží (tj. počva může být z různých materiálů s různou tuhostí a s různým stupněm defektů vzniklých důlní činností – reálná situace při důlní těžbě), se nabízí modelování s uvažováním pružného podkladu Winklerova typu, viz [1] až [4].

Nutno podotknout, že použití mechanického kontaktu (nelineární úloha) není vzhledem ke složitostem a neurčitostem stykové plochy vhodné. Z tohoto důvodu je uvažování jednoduššího pružného podkladu lepším a přesnějším modelem než aplikace mechanického kontaktu.

STYK SPODNÍ ČÁSTI VÝZTUŽE S POČVOU - MODEL SÍTĚ KONEČNÝCH PRVKŮ, OKRAJOVÉ PODMÍNKY A METODIKA ŘEŠENÍ
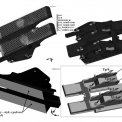
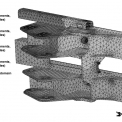
Dle zadaných rozměrů a podkladů dodavatele, byl vytvořen model spodní části výztuže a síť konečných prvků, viz obr. 3.

Celý model obsahuje 43 574 objemových čtyřstěnových prvků s meziuzly „tetra10“ a 82 406 uzlů s třemi hledanými neznámými posuvy v každém uzlu a to ve směru os kartézského souřadného systému.

Symbol „PODLOZI_K“ (obr. 3) značí působení pružného podkladu (tj. uložení na podloží o modulu podloží K [Nmm^–3] – nahrazení počvy spojitým pružným podkladem dle Winklerovy teorie, pro který byly zvoleny čtyři hodnoty: 0,1 Nmm^–3, 1 Nmm^–3, 3,5 Nmm^–3 a 6 Nmm^–3, a to tak aby respektovaly měkké až tuhé podloží. Vyšší hodnota K znamená vyšší tuhost podloží (počvy). Podloží zachycuje reakční účinky na dosedací ploše výztuže (tj. na dvou spodních obdélníkových plochách), viz také obr. 3. Podrobné informace o okrajových podmínkách (uchycení, zatížení, nesymetrie atp.) jsou uvedeny v knihách [3] nebo [4].

Dle zadání bylo tedy provedeno celkem 6 × 4 = 24 výpočtů (tj. pro šest variant A1 až B3 a to vždy ještě pro další čtyři subvarianty související s rozdílnou tuhostí podloží K: 0,1 Nmm^–3, 1 Nmm^–3, 3,5 Nmm^–3 a 6 Nmm^–3).

Materiál výztuže (tj. ocel) byl považován za homogenní, izotropní a lineární, kde modul pružnosti 210 000 MPa a Poissonovo číslo 0,3. Vliv plastických deformací oceli není třeba uvažovat.

Vzhledem ke zrychlení výpočtu bylo využito paralelizace a úloha byla řešena paralelně na čtyřech procesorech (běžný počítač) pomocí metody doménové dekompozice s aplikací FETI algoritmu (tj. moderní trend využití výkonu počítače pro řešení soustavy rovnic), viz rozdělení sítě konečných prvků na čtyři domény na obr. 4.

STYK SPODNÍ ČÁSTI VÝZTUŽE S POČVOU - VÝSLEDKY
Dle zadání z kapitoly byly provedeny výpočty různých variant styku spodní části mobilní výztuže s počvou, viz např. obr. 5 (výsledné celkové průhyby) a obr. 6 (průhyby v [mm] ve směru osy Y a také rozložení tlaků ve styku spodní části výztuže s počvou).

Dle Winklerovy teorie pružného podkladu totiž platí, že vypočtený tlak je přímo úměrný průhybu v (tj. p = -Kv). V obrázcích 6 je také vyznačena poloha maximálního tlaku p_MAX a minimálního tlaku p_MIN. Je zřejmé, že kontaktní tlak je proměnlivý.

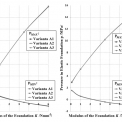
Z rozboru výsledků, viz podrobněji [3] a [4], lze stanovit následující. S velikostí modulu podloží K (tj. se zvětšující se tuhostí podloží) roste nelineárně velikost tlaku p_MAX (respektive nelineárně klesá velikost tlaku p_MIN) u variant A i B, viz obr. 7. Je zřejmé, že získané hodnoty tlaků ve styku s počvou se mění především v závislosti na velikosti modulu podloží. Podle průběhů tlaků ve styku s počvou, lze tedy považovat varianty A1 až A3 za téměř shodné (dále v textu nazýváno jako varianty A). Ze stejných důvodů lze také považovat varianty B1 až B3 za téměř shodné (dále v textu nazýváno jako varianty B).

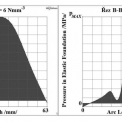
Zajímavý je také průběh tlaku p v řezu A-A po šířce styku a řezu B-B po délce styku důlní výztuže s počvou, viz obr. 8. Tyto řezy, provedené vždy přes polohu místa maximálního tlaku, jsou znázorněny na obr. 6d. Obrázek 8 tedy prokazuje značnou proměnlivost po šířce i délce stykové plochy spodní části výztuže. Tato podélná i příčná proměnlivost je také dobře patrná z obr. 6. Tlak p_MAX dosahuje u variant A i B maximálních teoretických hodnot p_{MAXA TEOR} = 15,857 MPa a p_{MAXB TEOR} = 14,1127 MPa, viz [3] a [4]. Uvedený výpočet je teoretické povahy (uvažuje konstantní rovnoměrnou a spojitou tuhost po obou obdélníkových stykových plochách důlní výztuže, dokonalý kontakt a samozřejmě ideální neporušené a hladké podloží bez poruch). Pro přesnější výpočet je vhodné tlaky p_{MAXA TEOR} a p_{MAXB TEOR} vynásobit koeficientem respektujícím reálnou situaci uložení konstrukce v dolech. Pro tento koeficient lze navrhnout hodnotu 1,15 (tj. bezpečné navýšení o 15 %). Pro reálný odhad maximálních hodnot tlaků pro varianty A, B pak platí:

p_{MAXA SKUT} = 1,15 x p_{MAXA TEOR} = 18,24 MPa,
p_{MAXB SKUT} = 1,15 x p_{MAXB TEOR} = 16,23 MPa,

kde p_{MAXA SKUT} respektive p_{MAXB SKUT} jsou tedy odhady skutečných maximálních tlaků působících ve styku výztuže s počvou pro velmi tuhá podloží (situace kdy K = 6 Nmm^–3), které lze použít pro další potřebu (např. výpočet pevnosti podkladu počvy atp.). Nutno podotknout, že takto vypočtené hodnoty p_{MAXA SKUT} a p_{MAXB SKUT} mají jen lokální charakter (tj. vyskytují se jen jako lokální špičky).  Vzhledem k obvyklé neznalosti a velké variabilitě vlastností podloží v dolech, je vhodné pro návrhové výpočty používat hodnoty p_{MAXA SKUT} respektive p_{MAXB SKUT}.

ZÁVĚR
Uvedeným postupem byly pomocí MKP stanoveny tlaky ve styku mobilní důlní výztuže s počvou a použity při návrhu provozu a posouzení uhelných slojí v daném dole. Blíže viz [3] nebo [4].

Článek vznikl v rámci projektu Ministerstva průmyslu a obchodu ČR FT-TA4/018 „Moderní trendy zvyšování spolehlivosti zařízení pro povrchovou těžbu užitkových nerostů“.

LITERATURA:
[1] Frydrýšek, K.: Nosníky a rámy na pružném podkladu 1 (Beams and Frames on Elastic Foundation 1, Faculty of Mechanical Engineering, VŠB – Technical University of Ostrava, ISBN 80-248-1244-4, Ostrava, Czech Republic, 2006, pp. 463
[2] Frydrýšek, K., Jančo, R.: Nosníky a rámy na pružném podkladu 2 (Beams and Frames on Elastic Foundation 2), Faculty of Mechanical Engineering, VŠB – Technical University of Ostrava, ISBN 978-80-248-1743-9, Ostrava, Czech Republic, 2008, pp. 516
[3] Frydrýšek, K., Nikodým, M.: Beams and Frames on Elastic Foundation 3 (Nosníky a rámy na pružném podkladu 3), ISBN 978-80-248-2257-0, VŠB – Technical University of Ostrava, Ostrava, Czech Republic, 2010, pp. 611
[4] Frydrýšek, K., Fries, J.: Aplikace konstrukcí na pružném podkladu, ISBN 978-80-248-2361-4, VŠB – Technical University of Ostrava, Ostrava, Czech Republic, 2010, pp. 204

Determination of Pressures in the Contact Between the Powered Mining Supports and Foot-wall
Pressures in the contact between the powered mining supports and foot-wall were determined in article by the means of MKP and were used during the operation proposal and corner lodges in particular mine.

Autor

• Doc. Ing. Frydrýsek Karel Ph.D.