Stabilita tenkostenných rúr vyplnených betónom
Rubrika: Projektování
V článku sú prezentované výsledky teoretickej analýzy lokálnej a globálnej stability centricky tlačených stĺpov štvorhranného obdĺžnikového prierezu bez uvažovania začiatočných geometrických imperfekcií. V práci je predstavená teória pružných kritických napätí pri lokálnom vydúvaní pravouhlých stenových prvkov namáhaných rovnomerným tlakovým zaťažením. Taktiež je uvedená numerická metóda výpočtu súčiniteľa kritického napätia pomocou diferenciálnej rovnice štíhlej steny s rôznym uložením po obvode. Pre modelovanie správania sa kompozitných prvkov bol použitý výpočtovo – grafický softvér ABAQUS. Analyzované stĺpy sú zaťažované tlakovou silou, ktorá sa vnáša rôznymi spôsobmi do kompozitného prierezu.
Využívanie inovatívnych nosných konštrukcií v pozemných a dopravných inžinierskych stavbách je stále aktuálnejšie, pretože sú hospodárnejšie a využívajú najnovšie výsledky vedy a výskumu. K takýmto konštrukciám patria aj kompozitné konštrukcie, tvorené efektívnym spojením dvoch alebo viacerých materiálov, napríklad ocele a betónu. Kompozitné stĺpy sú veľmi dôležitou súčasťou kompozitných konštrukcií a sú široko používané pri výstavbe výškových budov a mostných konštrukcií v miestach s vysokým tlakovým zaťažením s relatívne malými ohybovými momentmi. Do tejto kategórie môžeme zaradiť aj oceľové rúry pravouhlého prierezu vyplnené betónom. Takéto konštrukčné prvky majú svoje prednosti oproti prázdnym oceľovým rúram, ako je to uvedené v prácach [1] a [2], ale jednou z hlavných statických výhod je vyššia odolnosť proti strate lokálnej a globálnej stability.
V súčasnosti sa problematike kompozitných stĺpov venujú viaceré práce [3 – 5]. Sakino a kol. [6] sa venoval problematike krátkych centricky tlačených rúr vyplnených betónom. Storozhenko a kol. [7] a Liu a kol. [8] vykonali experimentálne skúšky stĺpov z vysokopevnej ocele a betónu, ktoré boli vystavené excentrickému zaťaženiu. Ellobody a Young [9] vo svojej štúdii predstavili dostatočne presný nelineárny model (pomocou metódy konečných prvkov) správania sa centricky tlačených kompozitných stĺpov s pravouhlým a kruhovým prierezom.
Eurocode 4 [10] umožňuje navrhovať kompozitné prierezy s kompaktnou oceľovou časťou. Autori Kanishchev a Kvočák v práci [1] ukázali, že pre hospodárnejší návrh stĺpov zo štvorhranných rúr vyplnených betónom je možné využiť aj prierezy triedy 4 (podľa normy STN EN 1993-1-1 [11]), čo je už mimo platnosti Eurocode 4.
LOKÁLNA STABILITA TLAČENÝCH PRAVOUHLÝCH STIEN
Základné princípy navrhovania prierezov 4. triedy založil Bryan [12], ktorý spracoval analýzu pružných kritických napätí σcr pri lokálnom vydúvaní dlhých pravouhlých stenových prvkov s jednoduchými (kĺbovými) podperami všetkých hrán pri pôsobení rovnomerného tlakového zaťaženia. Vzťah pre kritické napätia (1) zahrňuje rôzne okrajové podmienky a distribúciu síl prvku pomocou súčiniteľa kritického napätia kσ:
![]() (1).
(1).
Minimálne hodnoty súčiniteľa kritického napätia kσ sú uvedené v STN EN 1993-1-5 [13]. V prípade vnútorných tlačených časti prierezov (stena pravouhlej rúry) tento súčiniteľ sa mení od kσ = 4 pri čistom tlaku až do kσ = 23,9 pri kombinácii tlaku a ohybu. Tento súčiniteľ je možné používať pri prázdnej štvorhrannej rúre. Keď táto rúra bude vyplnená betónom (vnútorné podopretie po výške steny oceľovej časti prierezu zmení okrajové podmienky jej uloženia z kĺbového pri prázdnej rúre na skoro votknutie pri vyplnenej betónom), táto norma neposkytuje hodnotu kσ.
Stabilita kĺbovo podopretých tlačených pravouhlých stien
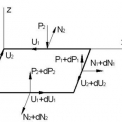
Problematike lokálneho vydúvania štíhlych tlačených stien bola venovaná výskumná práca Timoshenko [14], kde bola predstavená diferenciálna rovnica štíhlej steny s dĺžkou a, šírkou b (obr. 1a), ktorá je kĺbovo uložená po obvode:
![]() (2),
(2),
kde w je priehyb štíhlej steny, [m]; N je tlaková sila, [kN].
Tuhosť steny C:
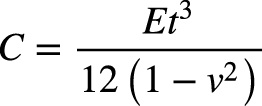 (3),
(3),
kde E je modul pružnosti ocele, [MPa]; t je hrúbka steny, [m]; v je Poissonov pomer.
Partikulárne riešenie diferenciálnej rovnice (2), reprezentujúce rovnováhu síl v jednom z možných vlastných tvarov steny:
![]() (4).
(4).
Dané riešenie spĺňa okrajové podmienky (obr. 1b, c): pri x = 0 a x = a → w = 0 a M1 = 0; pri y = 0 a y = b → w = 0 a M2 = 0. Pričom: N1 = –N; U1 = U2 = N2 = 0.
Dosadíme výraz (4) do rovnice (2) a nájdeme tlakovú silu N:
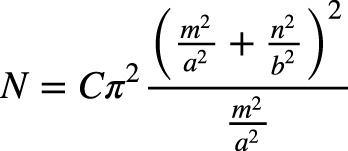 (5),
(5),
kde m a n sú polovlny po dĺžke a po šírke steny.
Zo všetkých možných vlastných tvarov rovnováhy síl v priereze steny treba nájsť ten, pri ktorom hodnota sily N bude minimálna, preto treba aby pravá časť rovnice (5) bola minimom. To bude vtedy, ak n = 1, čo je zrejmé, a hodnota m podľa práce [14] sa vyjadruje pomocou vzťahu (6). Z uvedeného vzťahu vychádza, že medzná hodnota dĺžky a, pri ktorej doska dostane prvý vlastný tvar, sa skladá z m polovĺn.
![]() (6).
(6).
Ak uvážime, že P/(t.b) = σ, kde σ je hodnota tlakového napätia, teda vzorec (5) upravíme s ohľadom na n = 1 a tuhosť steny:
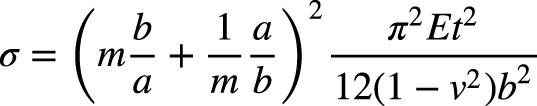 (7).
(7).
Podľa Eurocode 3 časť 1-5 [13] výraz (7) je hodnota pružného kritického napätia stien σcr = kσσE. Teda súčiniteľ kritického napätia kσ sa vyjadrí výrazom (obr. 2):
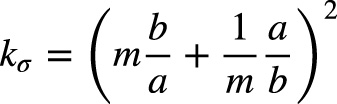 (8).
(8).
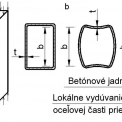
Tento súčiniteľ kritického napätia je možné použiť pri vydúvaní stien oceľového prierezu pravouhlej rúry (obr. 3b), pretože v danom prípade je umožnené pootočenie rohov prierezu, čo je kĺbové uloženie stien po obvode.
Stabilita pravouhlých stien votknutých na nezaťažených hranách a kĺbovo podopretých na hranách pri pôsobení tlakového zaťaženia
Ak je v rúre prítomné betónové jadro (obr. 3c), vytvorí sa kompozitný prvok, čím sa zabraní pootočeniu rohov oceľovej časti prierezu a okrajové podmienky uloženia stien oceľovej rúry sa zmenia v pozdĺžnom smere z kĺbového uloženia na čiastočné votknutie. Zmena okrajových podmienok uloženia steny z kĺbových na votknutie v nezaťažených hranách vyžaduje iné partikulárne riešenie diferenciálnej rovnice (2), ktoré podľa teórie Timoshenka [14] bude mať tvar:
![]() (9).
(9).
Partikulárne riešenie (9) spĺňa okrajové podmienky na priečnych hranách steny (obr. 1) pri x = 0 a x = a a na pozdĺžnych hranách y = 0 a y = b → w = 0 a ðw / ðy = 0.
Po uvážení vyššie uvedených okrajových podmienok dostaneme transcendentnú rovnicu (10), riešenie ktorej dáva súčiniteľ kritického napätia pri rôznych pomeroch strán štíhlej steny (tab.1):
![]() (10).
(10).
Tabuľka 1 – Závislosť súčiniteľa kritických napätí od pomeru strán steny pri m = 1
| a/b | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
| kσ | 9,44 | 7,69 | 7,05 | 7,00 | 7,29 | 7,83 | 7,69 |
MODELOVANIE KOMPOZITNÝCH PRVKOV
Simulácia správania sa pri centrickom zaťažení dvoch vzoriek prázdnych rúr a štyroch vzoriek rúr vyplnených betónom bola vytvorená vo vypočtovo-grafickom softvére ABAQUS 6.13-4 za účelom zistenia vplyvu betónového jadra na stabilitu kompozitných stĺpov bez uvažovania začiatočných geometrických imperfekcií. V danej teoretickej analýze bol namodelovaný pravouhlý prierez rúry RHS 200 × 100 × 3 (trieda 4 podľa [11]) s dĺžkou 3 500 mm.
Materiálové charakteristiky podľa Eurocode 3: akosť ocele S235; modul pružnosti 200 GPa; Poissonov pomer v pružnom stave 0,3. Správanie materiálu sa modelovalo ako pružnostno-plasticitné s lineárnym spevnením podľa [13]. Jadro kompozitných rúr sa modelovalo ako betónové s triedou betónu C20/25 podľa [15].
Pri modelovaní a vytvorení konečných prvkov bola použitá knižnica ABAQUS [16]: oceľová časť bola vytvorená z prvkov typu „shell“ S4R a betónová z prvkov typu „solid“ C3D8. Interakcia oceľovej a betónovej časti bola namodelovaná pomocou dvoch zložiek: „normálnej“ – ako tlak betónu na oceľovú časť a „tangenciálnej“ – ako šmykový odpor na rozhraní „oceľ-betón“. Koeficient trenia pri modelovaní sa uvažoval hodnotou 0,35.
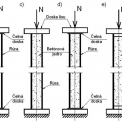
Okrajové podmienky boli simulované v súlade s obr. 4. Zaťaženie stĺpov bolo modelované ako krátkodobé s rovnomernou rýchlosťou cez platňu skúšobného lisu. Simulácia okrajových podmienok stien prázdneho prierezu bola vytvorená v dvoch variantoch: kĺbové uloženie čelných hrán stien (obr. 4a, c, e) a pomocou „fiktívneho“ privarenia čelnej dosky na obidvoch koncoch rúry, čo znamená, že bolo zabránené rotácii týchto hrán (obr. 4b, d, f).
VÝSLEDKY ANALÝZY
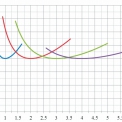
Pružné kritické napätia σcr a súčiniteľ kritických napätí kσ boli skúmané na širších stenách oceľovej časti prierezu. Taktiež bola zistená hodnota kritickej sily Ncr pôsobiaca na skúmané prvky pred začiatkom stáleho zvyšovania deformácií. Výsledky analýzy sú uvedené na obr. 5 – 10 a v tab. 2.
Tabuľka 2 – Výsledky analýzy
| Prvky | Deformácia | kσ | ABAQUS | |||
| podľa [13] | podľa [14] | Ncr [kN] | σcr [MPa] | kσ | ||
| Prázdna rúra | lokálna | 4 | - | 383,78 | 193,05 | 4,46 |
| Prázdna rúra s čelnými doskami | lokálna | 4 | - | 387,02 | 200,55 | 4,63 |
| Rúra vyplnená betónom | lokálna | - | 7 | 496,55 | - | - |
| globálna | - | - | 582,08 | - | - | |
|
Rúra vyplnená betónom s čelnými doskami |
lokálna | - | 7 | 561,55 | 222,86 | 5,15 |
| globálna | - | - | 652,34 | - | - | |
| Rúra vyplnená betónom (zaťaženie rúry) | lokálna | - | 7 | 400,94 | 221,87 | 5,13 |
| Rúra vyplnená betónom s čelnými doskami (zaťaženie rúry) | lokálna | - | 7 | 405,77 | 225,94 | 5,22 |
ZÁVER
Na základe výsledkov v (tab. 2) je možné konštatovať, že pri modelovaní prázdnych rúr bola zistená hodnota súčiniteľa kritického napätia kσ = 4,46, ktorá prevyšuje teoretickú hodnotu o 10,3 %. Privarené čelné dosky zvyšujú danú hodnotu do 4,63, čo prevyšuje teoretickú hodnotu o 13,6 %.
Betónové jadro v kompozitnom priereze zvyšuje lokálnu a globálnu stabilitu analyzovaných prvkov (tab. 2). Modelovanie týchto prvkov ukázalo, že strata lokálnej stability nastáva v plastickej oblasti správania sa materiálu. Táto deformácia sa prejavila bližšie ku koncom vyššie uvedených prvkov (obr. 7 – 10). Privarenie čelných dosiek (obr. 8) znížilo hodnotu kritických napätí z plastickej pružnej oblasti, ale súčiniteľ kritických napätí v porovnaní s prázdnymi rúrami sa zvýšil o 10,1 %. Hodnota kritickej sily (tab. 2) ukazuje aj na vysokú odolnosť vyššie uvedených stĺpov. V rúrach vyplnených betónom s tlačenou iba oceľovou častou prierezu analýza ukázala malý rozdiel hodnôt kσ v porovnaní s výsledkami pri zaťažení celého kompozitného prierezu. V porovnaní s teoretickou hodnotou kσ podľa teorii Timošenka [14], hodnoty získané z modelovania v ABAQUS sú o 25 % nižšie.
Príspevok bol podporený prostredníctvom projektu ITMS: 26220220124 „Vývoj mostov so zabetónovaným oceľovými nosníkmi modifikovaných tvarov“.
LITERATÚRA:
[1] Kanishchev, R. & Kvočák, V. 2015. Effects of Stability on the Resistance of Composite Concrete-Filled Rectangular Steel Pipes According to World Standards. Nara: IABSE, Elegance in Structures: 1–8.
[2] Garanzha, I., Vatin, N. 2014. Analytical methods for determination a load capacity of concrete-filled tubes under axial compression. Applied Mechanics and Materials Vol. 633 – 634: 965 – 971.
[3] Lee S. 2007. Capacity and the moment-curvature relationship of high-strength concrete filled steel tube columns under eccentri loads. Steel and Composite Structures 7(2): 135 – 160.
[4] Yang, Y. & Han L. 2009. Experiments on rectangular concrete-filled steel tubes loaded axially on a partially stressed cross-sectional area. Journal of Constructional Steel Research Vol. 65: 1617 – 1630.
[5] Uy, B. 2008. Stability and ductility of high performance steel sections with concrete infill. Journal of Constructional Steel research Vol. 64: 748 – 754.
[6] Sakino, K., Nakahara, H., Morino, S., Nishiyama, I. 2004. Behavior of centrally loaded concrete-filled steel-tube short columns. Structural Engineering ASCE Vol. 130(2): 180 – 188.
[7] Storozhenko, L.I., Ermolenko, D.A., Demchenko, O.V. 2014. Rabota pod nagruzkoi szhatych trubobetonnych elementov s usilennymi jadrami [The work under load of compressed pipe-concrete elements with strengthened cores]. Efficiency of resource energy of technology in the construction industry of region 4: 288 – 292.
[8] Liu, D., Gho, W.M., Yuan, J. 2003. Ultimate capacity of high-strength rectangular concrete-filled steel hollow section stub columns. Construction Steel Research Vol. 59(12): 1499 – 1515.
[9] Ellobody, E., Young, B. 2006. Nonlinear analysis of concrete-filled steel SHS and RHS columns. Thin-Walled Structures Vol. 44: 919 – 930.
[10] STN EN 1994-1-1 Navrhovanie spriahnutých oceľobetónových konštrukcií. Časť 1-1: Všeobecné pravidlá a pravidlá pre pozemná stavby. Bratislava: SUTN, 2005.
[11] STN EN 1993-1-1 Navrhovanie oceľových konštrukcií, Časť 1-1: Všeobecné pravidlá a pravidlá pre budovy. Bratislava: SUTN, 2006.
[12] Bryan, G.H. 1891. On the stability of a plane plate under trusts in its own plane, with applications to the „bukcling“ of the sides of a ship. Proceedings of the Lon-don Mathematical Society, Vol. 22, pp. 54 – 67.
[13] STN EN 1993-1-5 Navrhovanie oceľových konštrukcií, Časť 1-5: Nosné stenové prvky. Bratislava: SUTN, 2008.
[14] Timoshenko, S.P. Ustojchivost sterghnej, plastin i obolochek [Stability of rods, plates and shells]. Moskva, 1971: Nauka, 807 p.
[15] STN EN 1992-1-1 Navrhovanie betónových konštrukcií. Časť 1-1: Všeobecné pravidlá a pravidlá pre budovy. Bratislava: SUTN, 2005.
[16] Simulia Abaqus 6.13. 2013. Analysis Users Guide. Volume I.