Spriahnuté oceľobetónové stĺpy s plným oceľovým jadrom
Rubrika: Projektování
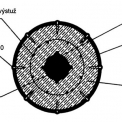
Spriahnuté oceľobetónové stĺpy typu – oceľové rúry vyplnené betónom, sú v praxi veľmi obľúbené z dôvodu uľahčenia technologického procesu betonáže do debnenia (obr. 1). Zo statického hľadiska oceľová rúra zachytáva priečne ťahy v betóne a vzniká tak ovinutie betónu oceľovým plášťom. Doplnením takéhoto prierezu plným oceľovým jadrom sa výrazne zvyšuje osová odolnosť spriahnutého stĺpa. V posledných rokoch je však známe, že takéto plné oceľové profily vykazujú aj nezanedbateľné zvyškové prierezové napätia už od výrobného procesu [4]. Z hľadiska dosiahnutia vyššej štíhlosti a odolnosti takýchto stĺpov je tu tiež možnosť použitia aj vysokopevnostných betónov. Súčasná norma pre navrhovanie spriahnutých oceľobetónových konštrukcií STN EN 1994-1-1 Navrhovanie spriahnutých oceľobetónových konštrukcií, časť 1-1: Všeobecné pravidlá a pravidlá pre budovy [2] sa nezaoberá s navrhovaním stĺpov z takýchto prierezov.
POUŽITIE SPRIAHNUTÝCH STĹPOV S PLNÝM OCEĽOVÝM JADROM V PRAXI
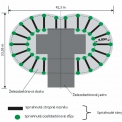
V súčasnej dobe sú tieto typy prierezov spriahnutých oceľobetónových stĺpov najčastejšie požívané vo vysokých budovách. Okrem spomínaných ich statických výhod poskytujú aj ďalšie výhody z praktického hľadiska, zo spôsobu realizácie a požiarnej bezpečnosti. Ide o stĺpy s hladkým povrchom, čiže nevyžadujú dodatočné úpravy pred finálnymi povrchovými úpravami. Umožňujú rýchlejšiu realizáciu výstavby. Z hľadiska požiarnej bezpečnosti nevykazujú špeciálne opatrenia. Uvedieme niekoľko príkladov použitia na niektorých stavbách v Európe. Patria k nim napríklad Post Tower, Bonn, Nemecko (obr. 2, obr. 3) alebo Millennium Tower, Viedeň, Rakúsko (obr. 4, obr. 5, obr. 6). V posledných rokoch boli na Slovensku takéto typy stĺpov použité pri výstavbe budovy v Bratislave, Národnej banky Slovenska. Jednalo sa o oceľový plný kruhový prierez, ktorý bol obalený železobetónom. Spolupôsobenie bolo zabezpečené privarenými oceľovými tŕňmi (obr. 7). V niektorých prípadoch boli tieto stĺpy po výške previazané so stenovým systémom.
NAVRHOVANIE SPRIAHNUTÝCH OCEĽOBETÓNOVÝCH STĹPOV Z OCELE VYŠŠEJ PEVNOSTI
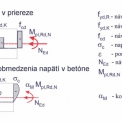
Navrhovanie spriahnutých oceľobetónových stĺpov zjednodušenou metódou podľa STN EN 1994-1-1,[2] je riešené na základe interakčnej krivky odolnosti prierezu za predpokladu plastickej odolnosti materiálov a zanedbaní nekonštantného priebehu napätí v jednotlivých materiálových častiach prierezu. Vplyv skutočného priebehu napätí v priereze a obmedzenie napätí v betóne sú okrem iného zahrnuté v korekčnom faktore ohybovej odolnosti aM = 0,9. Štúdie preukázali, že toto zjednodušenie pri prierezoch z konštrukčnej ocele vyšších pevností ako S355 nevedie k bezpečnému návrhu. Pri centricky zaťažených spriahnutých stĺpov z vysokopevnostnej ocele nie je potrebná žiadna úprava zjednodušenej návrhovej metódy. V prípade takýchto stĺpov zaťažených ohybovým momentom je však nutné uvažovať s prísnejším korekčným faktorom ohybovej odolnosti αM = 0,8. Týka sa to spriahnutých stĺpov s konštrukčnou oceľou S420 a S460 [5]. Obmedzenie napätí v betóne spôsobuje pomerne veľkú pružnú oblasť v oceľovom priereze. V prípade plného oceľového jadra v strede spriahnutého prierezu je tento vplyv obzvlášť výrazný (obr. 8).
Dochádza tu k výraznému rozdielu, pri porovnaní s pôvodným predpokladaným plastickým rozdelením napätí v priereze. V kombinácii so značným vplyvom reziduálnych napätí v oceľovom jadre nie je možné bezpečne použiť žiadny z uvedených korekčných faktorov αM, ktoré uvádza [2].
AKTUÁLNE ODPORÚČANIA PRE NAVRHOVANIE SPRIAHNUTÝCH STĹPOV S PLNÝM OCEĽOVÝM JADROM PODĽA STN EN 1994-1-1 ZJEDNODUŠENOU METÓDOU
Korekčný faktor ohybovej odolnosti prierezu αM
Ako bolo uvedené v predchádzajúcej časti, z dôvodu obmedzenia napätí v betónovej časti spriahnutého prierezu je výsledná odolnosť prierezu stanovená redukovanou plastickou odolnosť prierezu pomocou korekčného faktora αM podľa STN EN 1994-1-1, [2] (obr. 8). Pre prierezy s konštrukčnou oceľou do S355 je αM = 0,9 a s konštrukčnou oceľou do S460 je αM = 0,8.
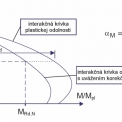
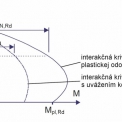
Vzhľadom k možnej rôznej veľkosti oceľového jadra v spriahnutých stĺpoch s plným oceľovým jadrom sa môže výrazne meniť pomer oceľovej časti k betónovej časti v priereze stĺpa, čo vedie k výrazným rozdielom plastickej a redukovanej odolnosti takýchto prierezov. Z tohto dôvodu nie je možné v danom prípade stanoviť konštantný korekčný faktor plastickej odolnosti uvedeného prierezu. Numerickou nelineárnou analýzou boli stanovené redukčné súčinitele αM pre konkrétne prierezy [3] podľa tab. 1. Na obr. 10 až obr. 13 sú graficky znázornené výsledky extrémnych prípadov zo všetkých analyzovaných prierezov. Parciálny súčiniteľ spoľahlivosti pre betóny bol uvažovaný γc = 1,5. Pre oceľové časti prierezu, čiže oceľová rúra a oceľové jadro, bol uvažovaný parciálny súčiniteľ spoľahlivosti γa = 1,1. Uvedené parciálne súčinitele spoľahlivosti materiálov boli pre analýzu stanovené podľa platných nemeckých noriem.
|
Tab. 1 – Analyzované prierezy pre stanovenie korekčných faktorov αM [3] |
|||||
| Prierez | Oceľová rúra | Oceľové jadro | Betón | ||
| fy | Φ | fy,k | fc | ||
| MPa | mm | MPa | MPa | ||
| QS1a | RR406,4 x 8,8 | S235 | - | - | C30/37 |
| QS1b | RR406,4 x 8,8 | S235 | 1) | S235 | C30/37 |
| QS1c | RR406,4 x 8,8 | S235 | 1) | S460 | C30/37 |
| QS2a | RR406,4 x 8,8 | S235 | - | - | C60/75 |
| QS2b | RR406,4 x 8,8 | S235 | 1) | S235 | C60/75 |
| QS2c | RR406,4 x 8,8 | S235 | 1) | S460 | C60/75 |
| QS3a | RR406,4 x 8,8 | S235 | - | - | C100/115 |
| QS3b | RR406,4 x 8,8 | S235 | 1) | S235 | C100/115 |
| QS3c | RR406,4 x 8,8 | S235 | 1) | S460 | C100/115 |
| QS4a | RR406,4 x 8,8 | S460 | - | - | C30/37 |
| QS4b | RR406,4 x 8,8 | S460 | 1) | S235 | C30/37 |
| QS4c | RR406,4 x 8,8 | S460 | 1) | S460 | C30/37 |
| QS5a | RR406,4 x 8,8 | S460 | - | - | C60/75 |
| QS5b | RR406,4 x 8,8 | S460 | 1) | S235 | C60/75 |
| QS5c | RR406,4 x 8,8 | S460 | 1) | S460 | C60/75 |
| QS6a | RR406,4 x 8,8 | S460 | - | - | C100/115 |
| QS6b | RR406,4 x 8,8 | S460 | 1) | S235 | C100/115 |
| QS6c | RR406,4 x 8,8 | S460 | 1) | S460 | C100/115 |
| 1) Priemer plného oceľ. jadra: 50, 100, 150, 200, 250, 300 [mm] | |||||
Výsledky analyzovaných prierezov poukazujú, že korekčný faktor αM výrazne závisí od pevnosti betónu, prierezových rozmerov oceľového jadra a pomeru NEd/Npl,Rd. Na základe výsledkov bol stanovený vzťah (1) pre určenie korekčného faktora αM závislého od pevnosti materiálov spriahnutého prierezu a od veľkosti prierezu oceľového jadra:

kde:
αM0 – základný korekčný faktor ohybovej odolnosti, podľa tab. 2,
αN – korekčný faktor zohľadňujúci vplyv osovej sily, podľa tab. 2,
NEd – návrhová hodnota osovej sily [kN],
Npl,Rd – návrhová hodnota plastickej osovej odolnosti prierezu [kN].
|
Tab. 2 – Analyzované prierezy pre stanovenie korekčných faktorov αM0 a αN [3] (medziľahlé hodnoty interpolovať) |
|||||||
|
Pevnostná trieda ocele oceľového jadra |
fyd,K |
Pevnostná trieda betónu |
fcd |
dk/d = 0 | dk/d = 0,75 | ||
| αM0 | αN | αM0 | αN | ||||
| S235 | 218 | C30/37 | 20 | 0,90 | 0,10 | 0,85 | 0,15 |
| C60/75 | 40 | 0,90 | 0,25 | 0,80 | 0,15 | ||
| C100/115 | 60 | 0,90 | 0,40 | 0,75 | 0,15 | ||
| S460 | 418 | C30/37 | 20 | 0,85 | 0,25 | 0,70 | 0,20 |
| C60/75 | 40 | 0,85 | 0,35 | 0,60 | 0,20 | ||
| C100/115 | 60 | 0,85 | 0,45 | 0,50 | 0,20 | ||
| 0,10 ≤ dk/d ≤ 0,75 | |||||||
ODOLNOSŤ SPRIAHNUTÉHO STĹPA S PLNÝM OCEĽOVÝM JADROM NAMÁHANÉHO TLAKOVOU SILOU A OHYBOVÝM MOMENTOM
Odolnosť spriahnutého stĺpa namáhaného tlakovou silou a ohybovým momentom sa posudzuje podľa vzťahu:
kde:
MEd – návrhová hodnota maximálneho ohybového momentu,
Mpl,N,Rd – návrhová hodnota príslušnej plastickej ohybovej odolnosti prierezu pri zaťažení osovou silou NEd,
αM – korekčný faktor plastickej ohybovej odolnosti prierezu.
Pre určenie ohybového momentu podľa teórie 2. rádu uvádza norma imperfekcie tlačeného prúta v závislosti od jeho geometrie prierezu vo forme počiatočnej excentricity w0. Norma však neponúka žiadnu ekvivalentnú mieru imperfekcie pre prierezy spriahnutých stĺpov s plným oceľovým jadrom. Preto boli nelineárnou numerickou analýzou zisťované imperfekcie takýchto stĺpov s rôznymi štíhlosťami, veľkosťami prierezu oceľového jadra a pevnosťami materiálov [3]. Výsledky poukazujú na nasledovné vplyvy pre imperfekciu spriahnutého stĺpa s tuhým oceľovým jadrom:
- použitie konštrukčnej ocele s vyššou pevnostnou triedou ako S355 vedie k priaznivému zníženiu počiatočnej excentricity w0 (obr. 15, tab. 3)
- veľkosť profilu oceľového jadra do 200 mm priaznivo vplýva (znižuje) počiatočnú excentricitu stĺpa. Pri väčších prierezových veľkostiach oceľového jadra ako 200 mm sa počiatočná excentricita zvyšuje (tab. 3).
|
Tab. 3 – Porovnanie vplyvu veľkosti prierezu oceľ. jadra a triedy ocele na mieru imperfekcie stĺpa (betón C60/75, pomerná štíhlosť = 1,0) [3] |
|||
| Oceľová rúra | Oceľ. jadro [mm] |
Medza klzu ocele [MPa] |
L/w0 |
| CHS 406,4 x 8,8 | - | 360 | 434 |
| 90 | 454 | ||
| 110 | 499 | ||
| 250 | 466 | ||
| 300 | 385 | ||
| CHS 406,4 x 8,8 | - | 460 | 533 |
| 90 | 584 | ||
| 110 | 654 | ||
| 300 | 520 | ||
| CHS 660 x 7,1 | - | 360 | 416 |
| 200 | 576 | ||
| 400 | 396 | ||
| CHS 660 x 7,1 | - | 460 | 515 |
| 200 | 756 | ||
| 400 | 544 | ||
Pre spriahnuté oceľobetónové stĺpy s plným oceľovým jadrom bola stanovená podľa výsledkov základná imperfekcia L/400, ktorú je potrebné modifikovať podľa vzťahu (3) a tab. 4 v závislosti od triedy použitej konštrukčnej ocele, veľkosti prierezu plného oceľového jadra a pomernej štíhlosti spriahnutého stĺpa:

kde:
L – dĺžka stĺpa [m],
w0 – počiatočná excentricita zohľadňujúca imperfekciu stĺpa [m],
k1 – faktor zohľadňujúci pevnostnú triedu ocele (medziľahlé hodnoty interpolovať),
k2 – faktor zohľadňujúci veľkosť prierezu plného oceľového jadra,
k3 – faktor zohľadňujúci pomernú štíhlosť stĺpa.
|
Tab. 4 – Faktory pre určenie imperfekcie spriahnutého stĺpa s plným oceľovým jadrom [3] |
||
| Trieda ocele | S355 | k1 = 1,0 |
| S460 | k1 = 1,25 | |
|
Veľkosť prierezu dk oceľového jadra |
dk ≤ 200 mm | |
| dk > 200 mm | ||
|
Pomerná štíhlosť stĺpa |
k3 = 0,8 | |
Na základe vzťahu (3) a tab. 4 boli vypočítané miery imperfekcie stĺpov L/w0 v závislosti od použitej triedy ocele a veľkosti prierezu plného oceľového jadra, a pomernej štíhlosti stĺpa mrel. Výsledné hodnoty sú uvedené v tab. 5.
| Tab. 5 – Miery imperfekcie L/w0 v závislosti od triedy ocele, štíhlosti stĺpa a veľkosti prierezu oceľ. jadra | ||||||||||||
|
Priemer oceľ. jadra |
≤ S355 | S420 | S460 | |||||||||
| λrel | λrel | λrel | ||||||||||
| ≤ 0,5 | 1,0 | 1,5 | 2,0 | ≤ 0,5 | 1,0 | 1,5 | 2,0 | ≤ 0,5 | 1,0 | 1,5 | 2,0 | |
| 50 | 360 | 405 | 450 | 495 | 416 | 468 | 520 | 572 | 450 | 506 | 563 | 619 |
| 100 | 400 | 450 | 500 | 550 | 462 | 520 | 577 | 635 | 500 | 563 | 625 | 688 |
| 150 | 440 | 495 | 550 | 605 | 508 | 572 | 635 | 699 | 550 | 619 | 688 | 756 |
| 200 | 480 | 540 | 600 | 660 | 554 | 624 | 693 | 762 | 600 | 675 | 750 | 825 |
| 250 | 440 | 495 | 550 | 605 | 508 | 572 | 635 | 699 | 550 | 619 | 688 | 756 |
| 300 | 400 | 450 | 500 | 550 | 462 | 520 | 577 | 635 | 500 | 563 | 625 | 688 |
| 350 | 360 | 405 | 450 | 495 | 416 | 468 | 520 | 572 | 450 | 506 | 563 | 619 |
| 400 | 320 | 360 | 400 | 440 | 370 | 416 | 462 | 508 | 400 | 450 | 500 | 550 |
VÝPOČTOVÝ PROGRAM PRE POSUDZOVANIE SPRIAHNUTÝCH STĹPOV PODĽA UVEDENÝCH ODPORÚČANÍ ZJEDNODUŠENOU METÓDOU STN EN 1994-1-1
V programe Mathcad 14 bol vytvorený program pre posudzovanie oceľobetónových stĺpov s prierezom oceľovej rúry vyplnenej betónom s plným oceľovým jadrom.
Postup je vytvorený na základe zjednodušenej metódy navrhovania spriahnutých stĺpov podľa [2].
MATERÁLOVÉ CHARAKTERISTIKY JEDNOTLIVÝCH ČASŤÍ SPRIAHNUTÉHO PRIEREZU
- Parciálny súčiniteľ spoľahlivosti konštrukčnej ocele; γa = 1,0
- Parciálny súčiniteľ spoľahlivosti betónu; γc = 1,5
- Charakteristická hodnota medze klzu oceľovej rúry; fy = 420 MPa
- Návrhová hodnota medze klzu oceľovej rúry; fyd = 420 MPa
- Modul pružnosti oceľovej rúry; Ea = 210 GPa
- Charakteristická hodnota medze klzu oceľového jadra; fk = 420 MPa
- Návrhová hodnota medze klzu oceľovej rúry; fkd = 420 MPa
- Modul pružnosti oceľovej rúry; Ek = 210 GPa
- Charakteristická hodnota pevnosti betónu v tlaku; fck = 30 MPa
- Návrhová hodnota pevnosti betónu v tlaku; fcd = 20 MPa
- Stredná hodnota pevnoti betónu v tlaku; fcm = 38 MPa
- Stredná hodnota modulu pružnosti betónu; Ecm = 33 GPa
PRIEREZOVÉ CHARAKTERISTIKY JEDNOTLIVÝCH ČASTÍ SPRIAHNUTÉHO PRIEREZU
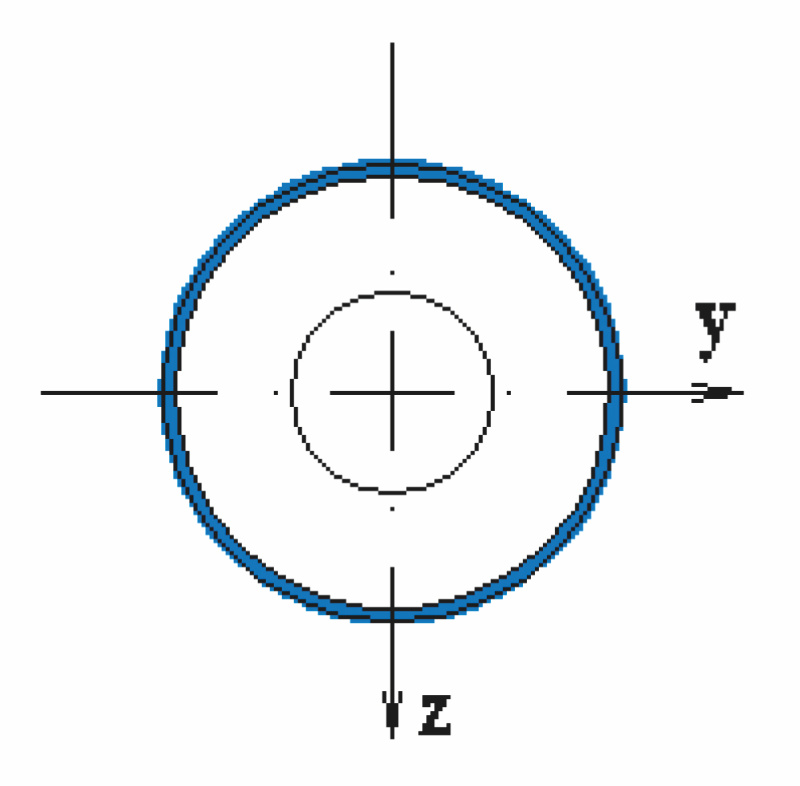
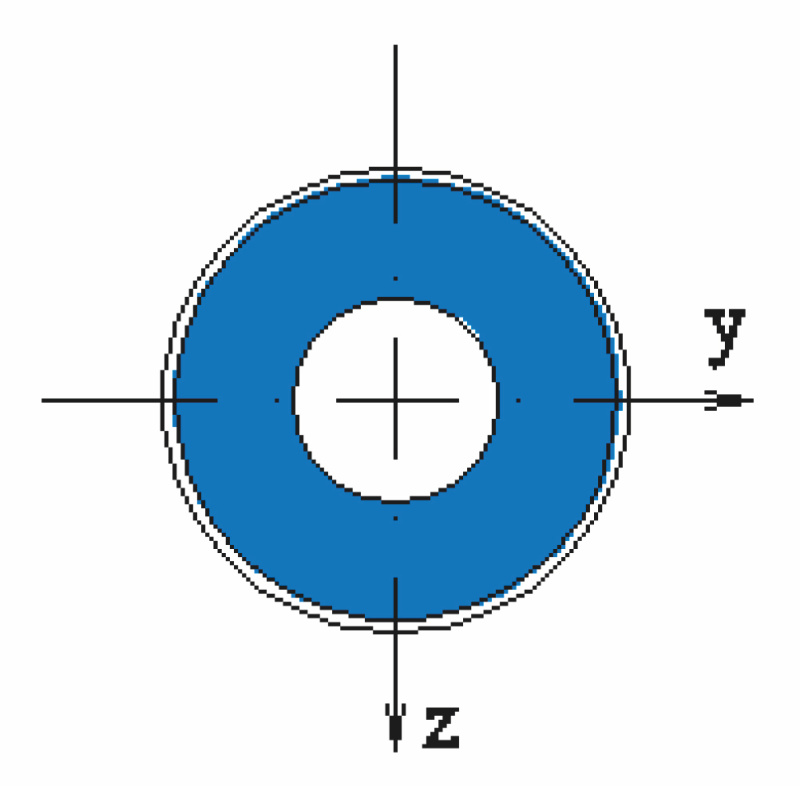
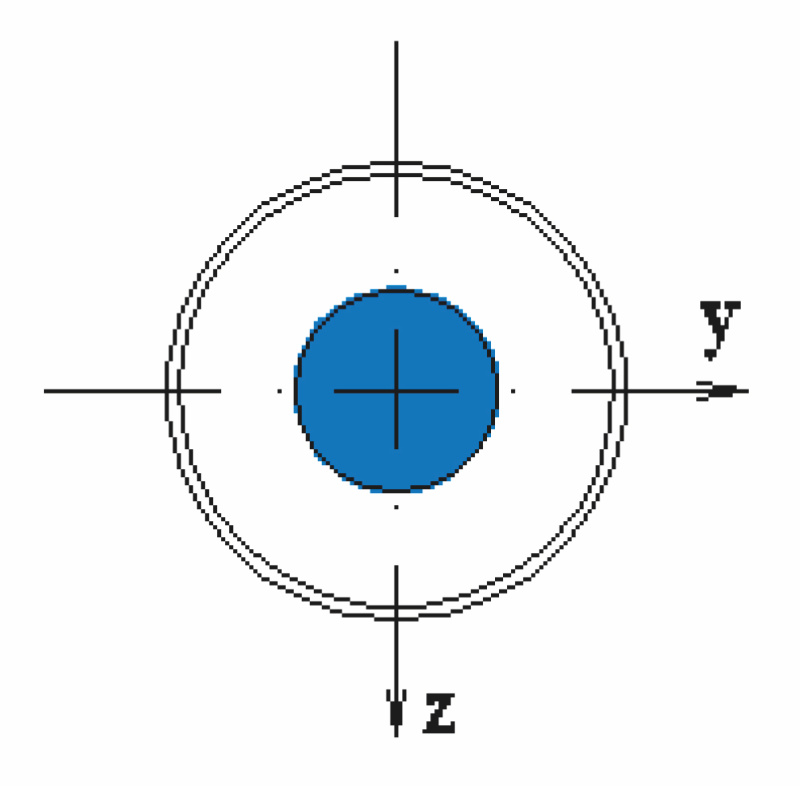
| a) | b) | c) |
 |
 |
 |
a) Prierez oceľovej rúry:
- Prierezová plocha; Aa = 0,017 m2
- Kvadratický moment zotrvačnosti; Ia = 5,306 . 10–4 m4
- Polomer zotrvačnosti prierezu; ia = 0,176 m
- Plastický prierezový modul; Wpl.a = 2,718 . 10–3 m3
b) Prierez betónovej časti:
- Prierezová plocha; Ac = 0,115 m2
- Kvadratický moment zotrvačnosti; Ic = 2,341 . 10–3 m4
- Polomer zotrvačnosti prierezu; ic = 0,143 m
- Plastický prierezový modul; Wpl.c = 0,015 m3
c) Prierez oceľového jadra:
- Prierezová plocha Aak = 0,071 m2
- Kvadratický moment zotrvačnosti Iak = 3,976 . 10–4 m4
- Polomer zotrvačnosti prierezu iak = 0,075 m
- Plastický prierezový modul Wpl.ak = 4,5 . 10–3 m3
ODOLNOSŤ STĹPA NAMÁHANÉHO KOMBINÁCIOU OSOVEJ SILY A OHYBOVÉHO MOMENTU
Maximálna ekvivalentná imperfekcia prúta:
- súčiniteľ zohľadňujúci pevnostnú triedu ocele plného oceľového jadra k1 = 1,200
- súčiniteľ zohľadňujúci vplyv veľkosti priemeru plného oceľového jadra k2 = 1,250
- súčiniteľ zohľadňujúci vplyv pomernej štíhlosti stĺpa k3 = 0,941
Miera imperfekcie: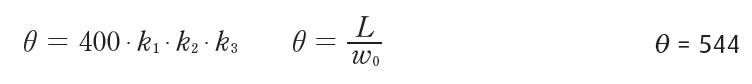
Návrhová hodnota celkovéhp ohybového momentu podle teórie II. rádu (všeobecná metóda):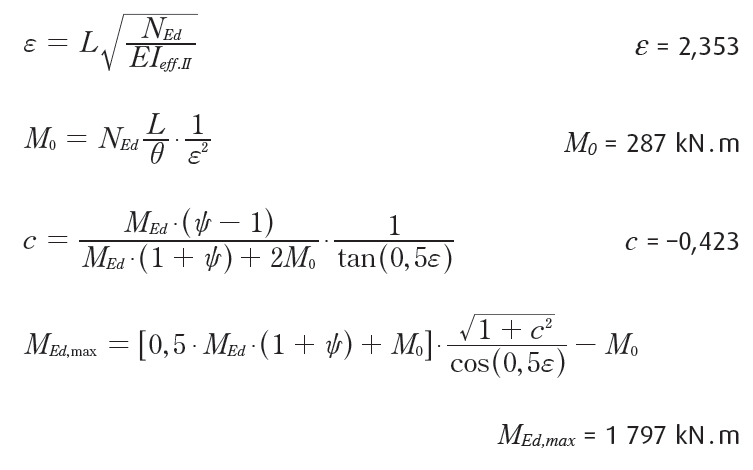
Korekčný faktor ohybovej odolnosti:
Podmienka odolnosti:
Odolnosť prúta na ohyb tlak = VYHOVUJE
Táto práca bola podporovaná Agentúrou na podporu výskumu a vývoja na základe Zmluvy č. APVV-0442-12.
LITERATÚRA:
[1] Frólo J. :Odolnosť spriahnutých oceľobetón. stĺpov s plným oceľovým jadrom, Projekt dizertačnej práce, SvF STU 2014,s.61
[2] STN EN 1994-1-1 Navrhovanie spriahnutých oceľobetón. konštrukcií, časť 1-1: Všeobecné pravidlá a pravidlá pre budovy, SUTN, 2006
[3] LIPPES M. :Zur Bemessung von Hohlprofil – Verbundstutzen aus hochfesten Stahlen und Betonen, Institut fur Konstruktiven Ingenieurbau Bergische Universitat Wuppertal, XI., 2008
[4] HANSWILLE, G., LIPPES, M.:Design of composite columns made of concrete filled tubes with inner massive core profiles and high strength materials, Inter. conference on composite construction in steel and concrete, Devil´s Thumb Ranch in Tebernasch, Colorado, July, 2008
[5] BERGMANN, R.,HANSWILLE, G.: New design method for composite columns including high strength steel, Internat. confernce composite construction in steel and concrete V., South Africa, 2004
Coupled Reinforced Concrete Beams with a Full Steel Core
Coupled reinforced concrete beams of the type – steel pipes filled with concrete are very popular in practice due to simplification of concreting to a falsework process (Fig. No.1). From the point of view of statistics, a steel pipe absorbs transverse tensile forces thus entwining of concrete with steel shell is performed. Adding a full steel core to such cross section, axis endurance of coupled beam significantly improves. During the course of last years it came out that these full steel profiles also show significant residual cross cut tensions already during a production process [4]. From the aspect of reaching higher sleekness and endurance of such beams, there is also possibility of using high-strength concretes. A current norm for designing of coupled reinforced concrete constructions STN EN 1994-1-1 Designing Coupled Reinforced Concrete Constructions, part 1-1: General Regulations and Regulations for Buildings [2] does not deal with designing of beams with such cross sections.















![Obr. 10 – Plastická a nelineárna odolnosť prierezu QS1a [3]](/PublicFiles/UserFiles/image/K/2014/k314/122x122_gram10.jpg)
![Obr. 11 – Plastická a nelineárna odolnosť prierezu QS6a [3]](/PublicFiles/UserFiles/image/K/2014/k314/122x122_gram11.jpg)
![Obr. 12 – Plastická a nelineárna odolnosť prierezu QS1b [3]](/PublicFiles/UserFiles/image/K/2014/k314/122x122_gram12.jpg)
![Obr. 13 – Plastická a nelineárna odolnosť prierezu QS6c [3]](/PublicFiles/UserFiles/image/K/2014/k314/122x122_gram13.jpg)
![Obr. 15 – Porovnanie počiatočných excentricít analyzovaných stĺpov s konštrukčnou oceľou S355 a S460 [3]](/PublicFiles/UserFiles/image/K/2014/k314/122x122_gram15.jpg)







