Řešení interakce plošných konstrukcí s podložím

• Foto

Toto rozdělení ale nesouvisí jen se zatížením, ale také s relativní tuhostí základu a horní stavby vůči podloží, s fyzikálními vlastnostmi podloží (heterogenitou, geologickými zlomy), s existencí sousedních staveb, apod. Proto je nutno při návrhu a posouzení jakékoliv konstrukce, která je ve styku s podložím, neřešit tuto konstrukci izolovaně, ale zabývat se jejich vzájemnou interakcí. To je v praxi reflektováno jen v omezené míře – brání tomu jisté mezery v teoretických podkladech, neexistence vhodné metodologie včetně softwarových nástrojů a velmi často nedostatek relevantních údajů o vlastnostech podloží. To vše je ještě navíc umocněno silnou prostorovou variabilitou. Posledně jmenovaná skutečnost vedla v posledním desetiletí k častější aplikaci stochastických metod při analýze geomechanických problémů i otázek interakce.

V našem prostředí došlo k prvním aplikacím na základové železobetonové nosníky již před řadou let – viz [1] až [3]. Úroveň výpočetní techniky však tehdy neumožnila dostatečné rozvinutí problematiky jak po stránce výzkumné, tak odborné a praktické. Tento stav stimuloval rozvíjející se spolupráci Ústavu stavební mechaniky, Ústavu geotechniky FAST VUT v Brně a firmy FEM consulting, s. r. o.

NAVRHOVÁNÍ BETONOVÝCH ZÁKLADOVÝCH KONSTRUKCÍ
Úskalí statického výpočtu a jeho výstižnosti
Jmenujme nejprve obtíže, se kterými by se měl inženýr-statik při návrhu konstrukce základů vypořádat v zájmu dosažení dostatečně spolehlivého a přitom ekonomicky efektivního řešení:

1. Konstrukce horní stavby a její zatížení, vlastní základová konstrukce a základové prostředí (podloží) s případným přitížením jsou vždy v interakci – tvoří jeden systém, obecně nelineární. Vzájemně se tedy tyto součásti ovlivňují a dostatečně realistické stanovení pole napětí a přetvoření, a tudíž efektivní návrh/posudek není možný bez přihlédnutí k této skutečnosti.
2. Působení zatížení a prostředí, materiálové i geometrické vlastnosti podléhají vždy většímu či menšímu rozptylu; nejvýraznější je to obvykle u vlastností podloží. Tuto okolnost lze zohlednit pomocí stochastických přístupů; to přináší také další výhodu – možnost kvantifikovat spolehlivost pro příslušné mezní stavy.

Poznamenejme, že současné normy/předpisy příslušné tomuto typu úloh se těmito otázkami zabývají jen velmi omezeně. V ideálním případě by pochopitelně bylo nutné při tvorbě výpočetního modelu respektovat obě tyto okolnosti a vytvořit tak postup podporující optimální návrh.

V současné době je však problémem ta skutečnost, že existují specializované geotechnické software, do kterých jsou implementovány pokročilé konstituční modely, které jsou schopny popsat chování zemin pro různé zatěžovací podmínky. Takto koncipované software jsou však především určeny pro modelování speciálních geotechnických úloh (hráze, svahy, podzemní výruby, tunelování a jiné podzemní objekty). Nedostatkem přitom je, že již zde nejsou dostatečně rozpracovány prvky pro modelování horní konstrukce, a proto je lze pouze v omezené míře využít pro posouzení betonových, ocelových či jiných konstrukcí.

Při zakládání běžných staveb nás nezajímají detailně děje uvnitř podloží, ale určující je vliv podloží na statiku stavební konstrukce. V těchto případech proto není nutná podrobná 3D analýza zemního masivu, ale je možné využít pro řešení interakce stavebních konstrukcí s podložím 2D modelu povrchu podloží. Tento postup podporuje i fakt, že pokud bychom chtěli modelovat podloží jako 3D (tedy pomocí prostorových konečných prvků), vzrostl by neznámý počet parametrů deformace tak výrazně, že v praktických případech bychom se dostali až za hranici časových a kapacitních možností současné výpočetní techniky.

Povrchový model podloží
Nejméně věrohodný je Winklerův model (bohužel velmi často aplikovaný), který považuje podloží za soustavu nekonečně hustých  pružinek nebo husté kapaliny. Tento model není schopen postihnout vznik poklesové kotliny nebo spolupůsobení sousedních objektů. Winklerův model zlepšil Pasternak, který za účelem vystihnutí smykových složek napětí přidal konstantu C₂.

Kolem roku 1975 zavedli do této problematiky nové pojetí Kolář a Němec [10]. Jde o sestavení takového povrchového 2D modelu, při jehož deformaci se vykoná stejná virtuální práce jako ve 3D podloží, přičemž lze vybudovat celou hierarchii parametrů C₁, C₂, C₃. Tento model podloží je podrobně popsán ve studiích [10–12]. Z důvodů dalšího výkladu zde proto uveďme jen vztah pro potenciální energii vnitřních sil 2D modelu s parametry C_1z a C_2x, C_2y (odpovídající winklerovské relaci pro svislou složku posunutí a pasternakovské relaci pro svislé smykové síly); w₀ (x,z) je sedání na povrchu:

V tomto pojetí je povrchový model podloží implementován do výpočetních systémů NEXIS 32 [7], Scia Engineer [8] (známého také pod dřívějším názvem SCIA.ESA PT), RFEM [9] a Renex3D [16] tak, že se potenciální energie nahromaděná v podloží přičte k potenciální energii konstrukce.

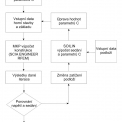
Zůstává tedy otázkou, jak co možná nejvěrohodněji zjistit dané parametry. Za tím účelem byl vytvořen program SOILIN [7, 8, 9, 13, 16], který na základě napjatosti pružného homogenního poloprostoru a normového modelu zeminy zjistí v jakémkoliv místě průběh sedání a z něho hledané parametry C. Protože tyto parametry ovlivňují kontaktní napětí a naopak průběh kontaktního napětí zpětně ovlivňuje sedání základové spáry a tím i parametry C, je nutné provést výpočet interakce konstrukce s podložím iterativně – viz obr. 1.

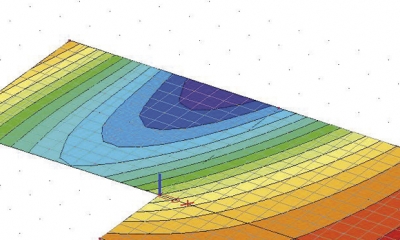
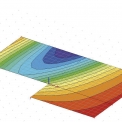
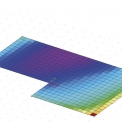
Střídavě tedy probíhá výpočet horní konstrukce včetně základu a výpočet parametrů C (které se následně automaticky přiřazují  příslušným 2D elementům modelujícím základovou konstrukci) a v převážné většině reálných úloh lze dospět z libovolného počátečního předpokladu k relativní shodě. Výchozí předpoklad ovlivní pouze počet iteračních kroků. Výsledkem výpočtu jsou vnitřní síly a deformace stavby, sedání povrchu podloží, kontaktní napětí v základové spáře v jednotlivých iteračních krocích a výsledné parametry interakce C – viz příklady na obr. 2 a 3.

Vliv nelinearity
Jak již bylo naznačeno v úvodu, kontaktní napětí v základové spáře (a tedy i rozložení a intenzita vnitřních sil) závisí mj. na tuhosti základu, horní stavby i podloží. Je proto vhodné/nutné uvažovat vliv: (a) nelineárního chování konstrukce – např. u železobetonové konstrukce namáhané na ohyb (nosníky, desky) dochází ke změně tuhostí po vzniku tahových trhlin – viz [1] a (b) nelineárního chování podloží – viz např. fyzikální model zeminy podle ČSN [14].

STOCHASTICKÉ MODELOVÁNÍ
Nejistoty podloží
Při modelování interakce staveb s podložím se zpravidla vždy objevuje nejistota pramenící především v určení příslušných geomechanických vlastností podloží. Je to způsobeno kvalitativními rozdíly mezi informacemi, které má statik k dispozici pro materiály horních staveb a pro materiály vrstev podloží, jejichž spolehlivost bývá výrazně nižší. Situaci komplikuje nejen fyzikální povaha zeminy, ale také i nemožnost podrobné znalosti geologického profi lu, protože v nejlepším případě jsou k dispozici výsledky několika sond a vlastní určení průběhu geologických vrstev a jejich mocností je jen otázkou odborného odhadu resp. zkušenosti zpracovatele inženýrsko-geologického průzkumu.

Znamená to, že úloha interakce konstrukce s podložím by se měla řešit s různými variantami geomechanických vstupních dat. Nepřímo k tomu nabádá i norma ČSN [14], která uvádí hodnoty modulů přetvárnosti E_def ve formě intervalů. Norma EC7 [15] v čl. 2.4.3 a 2.4.6 přímo uvádí, že při výpočtech se musí uvažovat s náhodnými změnami vlastností základové půdy, musí se vzít v úvahu nejistoty v geometrických údajích a že pro tyto hodnoty lze využít statistické metody. Z toho vyplývá, že problematika interakce konstrukce s podložím je typickým případem, kdy je potřeba ve výpočtu uvažovat i proměnlivost vstupních veličin, tedy řešit úlohu jako stochastickou. K tomu ale bližší pokyny norma neposkytuje.

Randomizace problému
Byl vypracován interface mezi programy FEM analýzy a pravděpodobnostním software FReET [4–6], který představuje simulační nástroj k řešení spolehlivostních problémů. Vstupní veličiny jsou modelovány jako náhodné s určitým teoretickým rozdělením pravděpodobnosti (normální, lognormální, Weibullovo aj.). Statistická závislost mezi nimi je popsána korelační maticí a zpracována metodou simulovaného žíhání. Pomocí stratifi kované simulace typu Monte Carlo (zpravidla Latin Hypercube Sampling) jsou realizovány tyto náhodné veličiny a poté použity ve výpočetním modelu analyzovaného problému, následuje část statistického a spolehlivostního vyhodnocení.

Citlivostní analýzu lze pak provádět metodou neparametrické pořadové korelace. Pravděpodobnostní software FReET je možno použít jako samostatně pracující modul vhodný pro řešení prakticky jakéhokoliv spolehlivostního problému. Je však orientován především na výpočtově náročnější problémy mechaniky kontinua, u nichž velký počet simulací klasické metody Monte Carlo nelze realizovat a kde reálné počty simulací musí být spíše v řádu desítek.

Pilotní výpočtová studie
Za účelem ověření vhodnosti navrženého postupu byla zpracována jednoduchá pilotní studie. Předmětem zkoumání byla obdélníková oblast 8 × 10 m. Hloubka výkopu se střední hodnotou 0,5 m se uvažovala s normálním rozdělením o variačním koeficientu 0,2. Pro geologický profil byly vybrány 3 vrstvy zeminy, jejichž vlastnosti byly vzaty ze směrných normových charakteristik. Pro tloušťky vrstev bylo odhadnuto normální rozdělení s variačním koeficientem 0,2. Modulům přetvárnosti bylo zadáno rozdělení rovnoměrné s mezemi, které odpovídají hodnotám udaným v normě. Ostatní veličiny byly zadány deterministicky opět s ohledem na normu. Výpočet byl proveden pro střed obdélníka, realizováno 1.000 simulací. Výsledné statistické charakteristiky sedání a parametru C_1z jsou včetně histogramů prezentovány na obr. 4 a 5.

Uvedené hodnoty ukazují, v jakých rozptylech se mohou výsledky přibližně pohybovat. Zaměříme-li se např. na základní veličinu ovlivňující interakci, což je parametr C_1z, je vidět, že může dosahovat hodnot rámcově od 3,5 až do 10,5 MN/m³. Tak velmi rozdílné hodnoty popisující podepření mají samozřejmě pro výpočet deformací a vnitřních sil horní konstrukce velký vliv a mohou konečné výsledky ovlivnit v řádech desítek procent, což je pro dimenzování alarmující. Je to ukázáno i v následujícím příkladu.

Statistická analýza interakce konstrukce s podložím
Možnosti analýzy uvedené v předcházející kapitole jsou zajímavé a poučné, ale nevypovídají o tom, jak se vlastně bude chovat konstrukce horní stavby. K tomu je potřeba přímo propojit pravděpodobnostní program s některým vhodným MKP systémem. Za tím účelem byly využity programy FReET a Scia Engineer a byla řešena přímo kompletní statistická analýza interakce horní konstrukce s podložím. Objektem zkoumání se tak nestaly parametry interakce a sedání, jako ve studii uvedené v předcházející kapitole, ale již přímo deformace a vnitřní síly horní konstrukce, které jsou pro analýzu stavby rozhodující.  Pro stochastickou analýzu byla vybrána jedna nádrž kruhového půdorysu z lokality Klobouky u Brna – viz [17]. V rámci geotechnického průzkumu [17] bylo pod nádrží provedeno pět sond statické penetrace.

Nejprve byla úloha řešena jako deterministická ve výpočetním systému Scia Engineer. Základová konstrukce byla modelována kruhovou betonovou deskou o průměru cca 34 m a tloušťce 400 mm, zatíženou ocelovou nádrží a náplní. Vše bylo počítáno v interakci s podložím, které bylo definované pěti sondami. Poloha, mocnost vrstev a geomechanické vlastnosti (E_def a v) byly vzaty z výsledků geologického průzkumu, který pro každou zeminu stanovil podle zatřídění zeminy příslušné průměrné hodnoty. Objemová tíha a součinitel strukturní pevnosti byly určeny odborným odhadem dle charakteru zeminy.

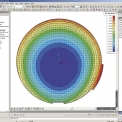
Pro výpočet interakce byl využit program SOILIN. Výsledné svislé deformace u_z po výpočtu interakce této základové desky s podložím jsou zobrazeny na obr. 6. Maximální průhyb základové desky činil 155 mm a největší hodnota dimenzačního momentu m_x,dim na spodním líci desky byla přibližně 195 kNm/m.

Před vlastní stochastickou analýzou bylo nutné definovat vstupy, tedy provést randomizaci úlohy, tj. uvážit možný rozptyl hodnot, jaký se v realitě může vyskytovat. To znamená, že pro každou z těchto pěti vrstev byly deformační modul E_def a Poissonovo číslo v uvažovány jako náhodné proměnné, celkem tedy bylo použito 10 náhodných proměnných. Pro získání statistických charakteristik rozdělení byla použita změřená data ve všech pěti penetračních sondách, pro každou náhodnou proměnnou tak byl k dispozici soubor 80–180 realizací. Na tato data byl následně aplikován Kolmogorov-Smirnovův test dobré shody pro nalezení nejvhodnějšího rozdělení pravděpodobnosti implementovaný v programu FReET. Jako nejvhodnější rozdělení se ve většině případů ukázalo Beta rozdělení, které bylo kvůli své flexibilitě použito u všech 10 náhodných proměnných.

Následně bylo spuštěno 2.000 simulací v programu FReET. Každá simulace zahrnovala generování padesáti náhodných veličin E_def a ν pro každou sondu a vrstvu a dále spuštění výpočetního jádra systému Scia Engineer, pomocí něhož byl proveden iterativní výpočet interakce základové desky s příslušným podložím. Toto podloží bylo defi nováno polohou, mocností vrstev a příslušnými  geomechanickými charakteristikami, přičemž v každé simulaci byla použita jiná sada veličin E_def a v. Výsledky 2000 výpočtů byly následně podrobeny statistickému vyhodnocení v programu FReET. Vypočtené statistické charakteristiky maximální svislé deformace desky a dimenzačního momentu m_x,dim v desce, včetně histogramů, jsou prezentovány na obr. 7 a 8.

Střední hodnota svislé deformace desky u_z,max je rovna 0,174 m, přičemž hodnota uz,d získaná deterministickým výpočtem je rovna 0,155 m. Vzhledem ke kladné šikmosti rozdělení je pravděpodobnost, že bude deterministická hodnota překročena, relativně vysoká, neboť činí 68 %.

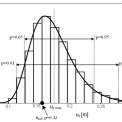
Střední hodnota maximálního dimenzačního momentu m_x,dim,max na spodním líci desky je rovna 212 kNm/m a hodnota m_x,dim,d, získaná deterministickým výpočtem, je rovna 195 kNm/m. Šikmost rozdělení je stejně jako pro deformaci uz kladná, což opět znamená vysokou pravděpodobnost překročení deterministické hodnoty, v tomto případě 66%.

Podobně jako u grafu u_z jsou i na obr. 8 vyznačeny 1%, 5%, 95%, 99% kvantily. Stojí za povšimnutí, že dimenzační moment 275 kNm/m, odpovídající 95% kvantilu (což je v podstatě běžně doporučovaná úroveň spolehlivosti), je o 41 % vyšší, než je maximální hodnota deterministického výpočtu (195 kNm/m). Pro návrh výztuže by pak bylo nutné použít právě tento extrémní moment. Je tedy zřejmé, že deterministický výpočet poskytuje hodnoty výrazně na straně nebezpečné.

Shrňme tedy, že v tomto konkrétním případě byla nejprve provedena deterministická interakce základové desky s podložím definovaným průměrnými hodnotami geomechanických veličin, které byly doporučeny v geotechnickém průzkumu [17]. Po provedení stochastické analýzy se ukázalo, že pravděpodobnost překročení deterministických hodnot je u sledovaných veličin u_z a m_x,dim více jak 60 %. Navíc hodnota momentu m_x,dim odpovídající 95% kvantilu byla oproti deterministickému o více než 40 % vyšší, což je zjištění za daných vstupních podmínek pro praxi alarmující – možná nespolehlivost návrhu při neuvažování náhodné proměnlivosti parametrů podloží je vysoká.

ZÁVĚR
Z výše uvedeného je patrné, že při řešení interakce konstrukce s podložím je nutno se zabývat náhodnou proměnlivostí vstupních dat podloží, neboť ta má výrazný vliv na deformace a vnitřní síly základové konstrukce. Také lze konstatovat, že navržený způsob použití 2D modelu podloží, implementovaný do programu SOILIN, umožňuje efektivně řešit interakci stavebních konstrukcí a podloží, což potvrzují i stovky jeho použití v rámci výpočetních systémů NEXIS 32, Scia Engineer (resp. SCIA.ESA PT) a RFEM. Teoretická odvození i praktické výpočty ukazují, že tento způsob výpočtu je akceptovatelný pro 3D, 2D i 1D modely konstrukcí, přičemž plně respektuje požadavky normy [14].

Tento příspěvek vznikl za podpory grantového projektu GAČR č. 103/08/0752 a výzkumného záměru MSM0021630519.

LITERATURA:
[1] Teplý, B., Materna, A., Keršner, Z.: K výpočtu základových konstrukcí, Beton a zdivo 4/1994, 30 –31
[2] Novák, D., Teplý, B.: Statistical analysis of random behavior of RC beams, Knižnice odbor a věd spisů VUT, roč 1991, sv A-51, p. 127–136
[3] Teplý, B., Materna, A., Keršner, Z., Novák, D.: Statistická analýza základových železobetonových nosníků, NUMEG 87, Vys. Tatry, 1987
[4] Novák, D., Vořechovský, M., Rusina, R.: Freet version 1.5 – User‘s Manual and Theory Manual. Brno/Červenka Consulting, 2007, http://www.freet.cz
[5] Novák, D., Vořechovský, M., Rusina, R.: Small-sample Probabilistic Assessment – software FREET, ICASP 9, 9th International Conference on Applications of Statistics and Probability in Civil Engineering, San Francisco, USA, Millpress, Rotterdam, 2003, 91–96
[6] Novák, D., Vořechovský, M., Rusina, R.: Small-sample simulation methods for statistical, sensitivity and reliability analyse. 3rd Probabilistic Workshop Technical systems Natural Hazards, Vienna, Austria, 2005, 51–60
[7] NEXIS 32 (Esa-Prima Win) 2005: Program system for the analysis of structure composed of 1D and 2D elements, SCIA Group nv, Industrieweg 1007, B-3540 Herk-de-Stad, Belgium
[8] SCIA ENGINEER 2008: Software System for Analysis, Design and Drawings of Steel, Concrete, Timber, Aluminium and Plastic Structures, SCIA Group nv, Industrieweg 1007, B-3540 Herk-de-Stad, Belgium
[9] RFEM 2006: Finite Elements for Plates, Shear Walls, Shells, Solids and Frameworks, Ingenieur-Software Dlubal GmbH, Am Zellweg 2, D-93464 Tiefenbach, Germany
[10] Kolář, V., Němec, I.: Studie nového modelu podloží staveb, ACADEMIA Praha, 1986, 184 s.
[11] Kolář, V., Němec, I.: Modelling of Soil-Structure Interaction, New York, Oxford, London, Amsterdam, Tokyo, ELSEVIER, 1989, 334 s. [12] Kolář, V., Němec, I.: Contact Stress and Settlement in the Structure – Soil Interface, Praha, Academia, Studie ČSAV 16.91, 1991, 160 s.
[13] Buček, J., Kolář ,V., Obruča, J.: Soilin Výpočet sedání a parametrů interakce podle norem ČSN, DIN a zásad EC7, Brno, FEM  consulting, s. r. o., 1993, 56 s.
[14] ČSN 73 1001 Základová půda pod plošnými základy, 1988, 75 s.
[15] EC7 Navrhování geotechnických konstrukcí, 1997, 146 s.
[16] RENEX3D, verze 1.03, leden 2009, Výpočet metodou konečných prvků pro stěny, desky a skořepiny v prostředí AutoCAD 2000 a vyšší, RECOC s. r. o., Seydlerova 2451/8, CZ 158 00 Praha 5, 155 s.
[17] GEOTREND s. r. o. 2004: Zpráva o geotechnickém průzkumu na lokalitě Klobouky u Brna – areál ČEPRO pro stavbu: „Obnova skladovacích kapacit PH a nádrž na ropu“

The solution for interaction of plane structures with the subgrade
The term interaction may be used for any mutual action of individual construction elements of building structure and determining how these elements influence each other. A typical case is considering the subgrade when calculating the upper structure. This is often quite difficult because the load of the base is mostly not reflected on the subgrade directly but it depends on the distribution of the effective stress along the footing bottom.

Autoři

• Ing. Arch. Buček Jiří
• Doc. Ing. Němec Ivan CSc.
• Ing. Rusina Radoslav Ph.D.
• Ing. Míča Lumír Ph.D.
• Prof. Ing. Novák Drahomír DrSc.
• Prof. Ing. Teplý Břetislav CSc.