Přístup k modelování a analýze železobetonových konstrukcí
Rubrika: Projektování
V předkládaném článku jsou srovnávány tři různé alternativy výpočetní analýzy prvků železobetonových konstrukcí, které jsou konfrontovány s publikovanými výsledky laboratorních zkoušek. Studovány byly nosníky s obdélníkovým průřezem a T‑průřezem a obdélníková stěna. Cílem příspěvku je porovnat potřebná vstupní data a získané výsledky.
V některých případech, např. u významných průmyslových zařízení [6], je potřebné posouzení statického chování železobetonové konstrukce s vyšší výstižností než jakou poskytují běžné normové postupy. Protože nelineárnímu modelování betonu je celosvětově a dlouhodobě věnována značná pozornost [4], je možné vybrat si z nejrůznějších typů materiálových modelů (například [3, 7, 11]), které jsou implementovány v řadě programových produktů.
Určitým problémem při praktickém použití je volba vhodného materiálového modelu pro danou úlohu, ale zejména stanovení výstižných vstupních dat, jejichž výstižnost má rozhodující vliv na kvalitu dosažených výsledků. Tento příspěvek si proto klade za cíl u několika vybraných příkladů experimentálně ověřených železobetonových prvků porovnat použitá vstupní data a ukázat jaké shody bylo dosaženo mezi naměřenými a vypočítanými výsledky.
MATERIÁLOVÉ MODELY
Při výpočtech byly použity tři různé materiálové modely. Z teorie nelineární lomové mechaniky [3, 5] vychází model SBETA poskytovaný výpočetním software Atena [9]. Zbývající dva materiálové modely byly pružno-plastické: model CONCRETE výpočetního software ANSYS [13], který je založen na podmínce plasticity a porušení podle Willama a Warnkeho [15] a model využívající Chen-Chenovy podmínky s Ohtaniho modelem zpevnění, který je implementován v software BSA vyvíjeném na VŠB-TU Ostrava [14].
VÝPOČETNÍ MODELY
Úlohy byly modelovány za předpokladu rovinné napjatosti a byly využívány čtyřuzlové konečné prvky [12] poskytované programy Atena a BSA. Pouze v případě modelů sestavených pro software ANSYS byly používány modely prostorové, neboť uvedený programový nástroj neumožňuje kombinovat materiálový model CONCRETE s konečnými prvky pro 2D úlohy. Proto byly použity osmiuzlové prostorové konečné prvky SOLID65.
Při nelineárních výpočtech byla ve všech případech využívána Newtonova-Raphsonova přírůstkově-iterační metoda a bylo používáno silové zatížení.
POUŽITÁ VSTUPNÍ DATA
Rozsah údajů o parametry materiálu, které jsou postačující pro běžné normové výpočty, pro lineární výpočty zpravidla nedostačuje. Protože získání chybějících údajů je zpravidla obtížné, je možné v literatuře najít přibližné vztahy pro jejich určení (například lomovou energii [5]), případně tyto vztahy uvádí i autoři použitého software [9]. Problémem může být omezená platnost takových údajů jen na betony určitých parametrů. U software Atena byly přímo využívány hodnoty stanovené softwarem na základě zadané krychelné pevnosti. U modelů pro software ANSYS se využívaly níže definované vztahy podle [15] a [17]:
- Pevnost betonu v tlaku Fc (1)
- Pevnost betonu v tahu Ft (2)
- Pevnost betonu v dvouosém tlaku Fbc = 1,2 * Fc (3)
- Hydrostatický tlak σh = √3 * Fc, (4)
- Smykový koeficient pro otevření trhlin rt = 0,0 - 0,5 (5)
- Smykový koeficient pro uzavíraní trhlin rc = 0,5 - 0,9 (6)
- Jednoosý hydrostatický tlak drcení betonu F1 = 1,45 * Fc (7)
- Dvouosý hydrostatický tlak drcení betonu F2 = 1,725 * Fc (8)
- Faktor tahových trhlin 0,6 (9)
V dalším textu jsou pro úsporu místa uváděny pouze základní materiálové parametry. Hodnoty, které je možné získat automaticky nebo pomocí výše uvedených vztahů, byly vynechány.
Numerický příklad 1: Nosník obdélníkového průřezu
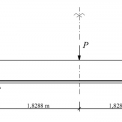
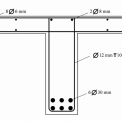
Experiment tvoří nosník zatížený osamělou silou uprostřed rozpětí [2]. Nosník má rozpětí 3,658 m, průřez nosníku je obdélníkový, výška průřezu je 0,508 m a šířka 0,203 m. Výztuž tvoří dvě výztužné vložky uložené u spodního okraje nosníku.
Schéma experimentu, polohy osamělé síly, okrajové podmínky a vyztužení zobrazuje obr. 1. Zatížení působí na horní hraně a má velikost 200 kN. Výchozí materiálovou charakteristikou betonu je modul pružnosti Ecm = 26 182 MPa [8]. Přehled ostatních použitých parametrů pro jednotlivé materiálové modely je uveden v tab. 1.
| Tab. 1 – Materiálové parametry betonu pro příklad 1 | ||||||
| Charakteristika/Model | Značka | Jednotka | Experiment | Concrete | SBETA | Pružnoplastický |
| Modul pružnosti | E | MPa | 26 182 | 26 182 | 26 182 | 26 182 |
| Pevnost betonu v tlaku | Fc | MPa | 33 | 40 | 19 | 20 |
| Pevnost betonu v tahu | Ft | MPa | 2,1 | 1,9 | 2 | |
Výztuž tvoří dva ocelové pruty o průměru 25 mm. Pracovní diagram oceli je ideálně pružnoplastický se zpevněním. Počáteční modul tuhosti má hodnotu Es1 = 203 255 MPa. Mez kluzu oceli je fy = 309,36 MPa. Po dosažení meze kluzu je modul tuhosti Es2 = Es1 /100.
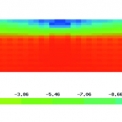
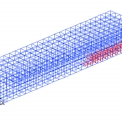
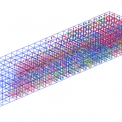
Porovnáním experimentu a výsledků jednotlivých výpočtů je možné konstatovat, že všechny mají dobrou shodu. Pro ilustraci provedených výpočtů jsou na obr. 3 a obr. 4 uvedeny výsledky pro pružnoplastický model betonu v programu BSA pro počáteční stav rozvoje plastické oblasti v tažené oblasti a stav, kdy dochází ke koncentraci tlaku na horním okraji. Další zatěžování pak vede do poslední fáze, kdy dojde k plastizaci výztuže a drcení betonu. Výsledky jednotlivých výpočtů se odlišují pouze v konečné fázi zatěžování.
Numerický příklad 2: Nosník s T- průřezem
Druhým modelovaným experimentem je nosník s T-průřezem zatíženým dvěma silami.
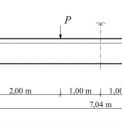
Celková délka nosníku je 7,04 m [1]. Výška nosníku včetně desky je 0,625 m, výška horní desky 0,11 m, šířka horní desky 1,00 m. Šířka žebra je 0,20 m. Geometrii testovaného nosníku, rozmístění sil a tvar průřezu zobrazuje obr. 5. Zatížení má hodnotu 600 kN. Poloha výztuže je patrná z obr. 6, kterou tvoří především hlavní nosná výztuž z šesti prutů o průřezu 30 mm.
Vlastnosti materiálu stanovené autory [1] a použité pro výpočty jsou uvedeny v tab. 2.
| Tab. 2 – Materiálové parametry betonu pro příklad 2 | ||||||
| Charakteristika/Model | Značka | Jednotka | Experiment | Concrete | SBETA | Pružnoplastický |
| Modul pružnosti | E | MPa | 31 380 | 31 380 | 31 380 | 31 380 |
| Pevnost betonu v tlaku | Fc | MPa | 23,4 | 40 | 24,5 | 23,4 |
| Pevnost betonu v tahu | Ft | MPa | 2,16 | 2,5 | 2,45 | 2,16 |
Poissonův součinitel pro beton se uvažoval 0,15. Výztuž se při výpočtu předpokládala ideálně pružnoplastická. Výztužné vložky o průměru 6 a 8 mm měly ocel s mezí kluzu fy = 482,45 MPa a zbylé výztužné vložky o průměru 12 a 30 mm měly mez kluzu fy = 567,77 MPa.
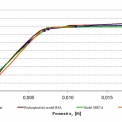
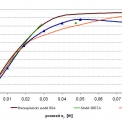
U druhého experimentu je shoda numerických řešení s experimentem nižší. Na pracovních diagramech je možné ilustrovat dobrou shodu zejména při nižších úrovních zatížení. Model SBETA dosahuje lepší shody v dosažené úrovni zatížení, pružnoplastický model dosahuje lepší shody tvaru pracovního diagramu zatěžovací křivky, ale vypočtené hodnoty jsou oproti experimentu nadhodnocené. V grafu je dále uveden zelený bod, který patří k výsledkům získaným pomocí modelu SBETA, ale u uvedeného stavu již nejsou splněny konvergenční kriteria. Pro ilustraci provedených výpočtů jsou zvoleny výsledky z programu ATENA. Obrázky 8 a 9 zobrazují vznik počátečních trhlin uprostřed rozpětí na dolním okraji a dále pak vznik smykové trhliny pro vyšší úrovně zatížení. Poloha trhlin v programu ANSYS je pak uvedena na obrázcích 10 a 11. Počáteční rozvoj trhlin zachycuje obr. 10 a stav rozvoje trhlin pro zatěžovací krok před kolapsem nosníku je zobrazen na obrázku 11.
Numerický příklad 3: Stěna
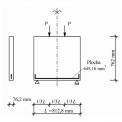
Posledním numericky modelovaným experimentem byla stěna zatížená dvěma silami [10]. Schéma experimentu je patrné z obr. 12. Rozměry stěny jsou 812,8 × 762 mm. Stěna má tloušťku 76,2 mm. Parametry betonu jsou uvedeny v tab. 3.
| Tab. 3 – Materiálové parametry betonu pro příklad 3 | ||||||
| Charakteristika/Model | Značka | Jednotka | Experiment | Concrete | SBETA | Pružnoplastický |
| Modul pružnosti | E | MPa | 31 724 | 31 724 | 31 724 | 31 724 |
| Pevnost betonu v tlaku | Fc | MPa | 27,31 | 45 | 27,2 | 27,31 |
| Pevnost betonu v tahu | Ft | MPa | 2,483 | 3,0 | 2,48 | 24,81 |
Celková plocha výztuže ve stěně je 645,16 mm2 a modul pružnosti je Es1 = 200 000 MPa. U oceli se předpokládá ve výpočtu pružnoplastický pracovní diagram s lineárním zpevněním Es2 = Es1/1 000. Mez kluzu oceli je 317,24 MPa. Zatížení P má velikost 350 kN.
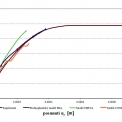
Srovnání vypočítaných pracovních diagramů s experimetem je uvedeno na obr. 13. Je patrná velmi dobrá shoda hodnot posunutí a zatížení pro lineární oblast zatížení a oblast počátku rozvoje trhlin. Při vyšších hodnotách zatížení se jednotlivé výpočty rozcházejí již výrazněji.
U uvedeného experimentu podstatně ovlivňuje dosažené výsledky také způsob modelování okrajových podmínek – podpor – kde vznikají velké koncentrace napětí. Rozvoj trhlin a vznik smykové trhliny jsou zobrazeny na obr. 14 a 15, který byly vytvořeny ve výpočetním systému ANSYS pro model CONCRETE.
ZÁVĚR
Provedené numerické analýzy u zvolených experimentů poskytly u použitých konstitutivních modelů betonu dobrou představu o jejich skutečném chování.
Oblast zatěžování, ve které docházelo k větším rozporům s experimentálními daty, leží již v oblasti speciálních aplikací, pro které nejsou pružno-plastické modely vhodné.
Je ovšem nutné upozornit, že ilustrovaná výstižnost jednotlivých modelů (zejména v případě pružnoplastického modelu v programu BSA) má platnost u běžných betonů, zatímco například u vysokopevnostních betonů mohou použité vztahy pro dopočet vstupních dat selhávat.
Na uvedených experimentech je také možné ilustrovat vyšší obtížnost vystižení chování konstrukce složitějších tvarů – zatímco u tvarově jednoduchého nosníku obdélníkového průřezu bylo dosaženo vynikající shody výpočtů a experimentu, u ostatních modelů jsou rozdíly větší. Je také patrné, že samotné použití 3D modelu nemusí nutně vést k lepším výsledkům než u vhodně sestaveného 2D modelu, jako tomu bylo u třetího příkladu.
Další problematickou oblastí, které může výsledky podstatně ovlivnit, je modelování podpor a zatížení, kdy bodové podpory, obvyklé u prutových modelů, musí být nahrazeny modelem co nejlépe odpovídajícím skutečnosti (velikost kontaktních ploch, tuhost podpor). Velikost roznášecích oblastí je patrná například z obrázků 8 a 9.
Získané výsledky budou využívány jakou součást podkladů pro modelování rozsáhlejších železobetonových konstrukcí.
Projekt byl realizován za finanční podpory ze státních prostředků České republiky prostřednictvím Studentské grantové soutěže v rámci specifického výzkumu na Vysoké škole báňské – Technické univerzitě Ostrava. Registrační číslo projektu je SP2011/74.
LITERATURA:
[1] Abdel-Rahman, H. H.: Computational Model for the Nonlinear Analzsis of Reinforced Concrete Flexural Slab systems, Ph.D. thesis, Dept. of Civil Eng., Univ. Coll. of Swansea, Swansea, 1982
[2] Barzegar F.: Layering of RC Membrane and Plate Elements in Nonlinear Analysis, Journal of the Struct. Div. 1988, Vol. 114, No. 11, p. 2474–2492
[3] Bazant, Z. P., Planas J.: Fracture and Size Effect in Concrete and Other Quasibrittle Materiále, Boca Raton,CRC Press, 1998
[4] CEB – FIP Model Code 1990: Design Code, by Comite Euro-International du Beton, Thomas Telford, 1993, ISBN: 978-0727716965
[5] Karihalo, O., B. L.: Fracture Mechanics and Structural Concrete, Essex: Longman Group Limited, 1995
[6] Králik J., Hukel D.: Nelineárna analýza interakcie oceľovej výstelky a železobetónovej steny šachty lokalizácie havárie za extrémneho pôsobenia tlaku a teploty, In Modelování v mechanice 2010, Mezinárodní konference, Ostrava: VŠB – TU Ostrava, 2010, ISBN 978-80-248-2234-1
[7] Hofstetter, G., Mang, H., A.: Computational Mechanics of Reinforced Concrete Structures, Wiesbaden: Vieweg, 1995, ISBN 3-528-06390-4
[8] Meguid Hekal S. A.: Solution of Plate Structures Respecting Real Material Properties, Disertační práce, Brno: Brno University of Technology, 1992
[9] Programový systém ATENA 2D: Theory Manual. Praha: Červenka Consulting, 2000
[10] Ramakrishnan, V., Ananthanarayana, Y. A.: Ultimate strength of deep beams in shear. J. ACI 65, 87–98, 1968
[11] Ravinger, J.: Programy – statika, stabilita a dynamika stavebných konštrukcií, Alfa, Bratislava, 1990
[12] Rombach, G.: Anwendung der Finite-Elemente-Methode im Betonbau, 2. Auflage, Berlin: Ernst & Sohn, 2007, ISBN 978-3-433-01701-2
[13] RELEASE 11 DOCUMENTATION FOR ANSYS, SAS IP, INC., 2007
[14] Sucharda, O., Brožovský, J.: Pružnoplastické modelování železobetonového nosníku: implementace a srovnání s experimentem. Sborník vědeckých prací VŠB-TUO, řada stavební. 2011, roč. 11, č. 1, s. 237–244, ISSN: 1213-1962
[15] Willam, K., J., Warnke, E., P.: Constitutive Model for the Triaxial Behavior of Concrete, Proceedings of International Association for Bridge and Structural Engineering, Bergamo, 1975
Approach to Modelling and Analysis of Reinforced Concrete Structures
In this presented article, three different alternatives of computer analysis of reinforced concrete structure elements are compared. These are confronted with published results of laboratory tests. The beams of a rectangular cross-section and T-section and a rectangular wall were studied. The aim of this contribution is to compare the required input data and results obtained.