Příspěvek k výpočetní optimalizaci rotačních skořepin

• Foto

Předkládaný článek se zabývá jedním z možných přístupů k optimalizaci konstrukcí: vychází z předpokladu, že základní geometrie konstrukce je dána předem a k optimalizaci tedy zbývá „jen“ navrhnout odpovídající rozměry jednotlivých konstrukčních prvků. Přitom je třeba respektovat fakt, že rozměry prvků a dílců jsou omezeny dostupným sortimentem stavebnin a konstrukčními zásadami a je tedy možné je definovat v podobě řady diskrétních hodnot. Také je obvykle potřebné respektovat vztahy mezi parametry jednotlivých prvků (například nutnost stejné tloušťky pro všechny prvky v určité části konstrukce). Po uplatnění uvedených předpokladů je možné vytvořit velmi mnoho variant modelu konstrukce s různými parametry konstrukčních prvků. Ty by bylo možné postupně posoudit a určit jejich cenu a následně vybrat nejlevnější variantu, která vyhoví požadavkům spolehlivosti. Aby byl takový postup časově únosný, je samozřejmě nutné co nejvíce využít možností výpočetní techniky.

Je samozřejmě dosti obtížné vytvořit obecný programový systém, který by byl schopen posuzovat a optimalizovat libovolné stavební konstrukce, proto je vhodnější zaměřit se na optimalizaci konkrétních typů konstrukcí. V článku je prezentován takovýto přístup a vyvinutý software, který vznikl v rámci studentské výzkumné aktivity na Fakultě stavební Vysoké školy báňské – Technické univerzity Ostrava. Oblast řešených úloh je proto omezena na rotačně symetrické skořepiny a byla uplatněna i některá další zjednodušení, která jsou uvedena v příslušných pasážích. V budoucnu se předpokládá další vývoj a rozšiřování vyvinuté metodiky a software na další typy úloh.

V dalším textu je popsáno modelování rotačních skořepin metodou konečných prvků, zvolený přístup k posuzování spolehlivosti konstrukce a metodika optimalizačního výpočtu. Uveden je i ilustrující příklad.

Výpočetní modelování
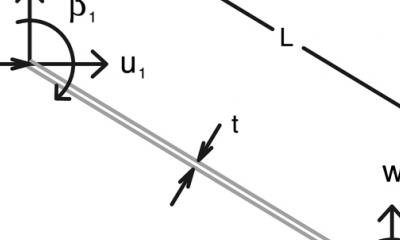
Výpočetní model konstrukce využívá metody konečných prvků [9]. Použity jsou dvojuzlové konečné prvky pro řešení rotačně symetrických úloh [7], které poskytují dobrý poměr mezi výpočetní náročností a přesností řešení. Každý uzel konečného prvku má tři stupně volnosti: posunutí ve směru svislém a ve směru radiálním a pootočení. Tento konečný prvek respektuje jak membránové, tak ohybové složky vnitřních sil.

Nevýhodou použití konečného prvku pro rotačně-symetrické úlohy je problematičtější zavádění nesymetrických zatížení do výpočtu. Jde sice o řešitelný problém, nicméně zde řešené úlohy se zaměřují jen na problémy s rotačně symetrickým zatížením a uložením konstrukcí.

Posouzení spolehlivosti
Při posouzení spolehlivosti konstrukce je možné vycházet buď ze vztahů definovaných technickými normami (obvykle Eurocode, které používají polopravděpodobnostní přístup) nebo použít přístup přímo využívající nástrojů matematické statistiky a teorie spolehlivosti. Podrobný postup a zásady použití pravděpodobnostních metod uvádí [10, 11]. Příkladem může být využití pravděpodobnostího výpočtu podle zásad metody SBRA [4, 5], které je použito v dále uvedeném demonstračním příkladu.

U železobetonových skořepin sloužících jako zásobníky kapalných látek je obvyklým požadavkem podmínka, že v materiálu nesmí vzniknout trhliny. Tato podmínka byla proto využita jako kritérium spolehlivosti v řešených úlohách – pokud v konstrukci vznikají trhliny, ta nesplňuje požadavky na vodotěsnost, a tedy neplní svoji základní funkci a nevyhovuje tak požadavkům návrhu.

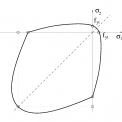
Na základě [8] bylo použito kritérium spolehlivosti v podobě nerovnice (1), která využívá prostorového stavu napjatosti. Pro potřeby posudku rotačních skořepin byly výrazy pro invarianty napětí (I₁ je první invariant tenzoru napjatosti, J₂ je druhý invariant deviátoru tenzoru napjatosti) vyjádřeny na základě napětí vznikajících na rotační skořepině. Hodnota fcm odpovídá meznímu napětí betonu na mezi vzniku trhlin.

Typický tvar podmínky (1) uvádíme na obr. 2 ve formě rovinného řezu podmínkou.

Výpočetní optimalizace
Proces výpočetní optimalizace vychází předpokladů, že základní geometrie konstrukce je dána předem, a že optimalizovány mohou být rozměrové parametry konstrukčních prvků, případně materiálové charakteristiky. Tyto parametry musí být možné popsat řadami diskrétních hodnot, což ovšem plně vyhovuje stavební praxi, kdy je možné volit z omezené řady diskrétních parametrů (průřezové charakteristiky dostupných typů válcovaných profilů, tloušťky betonových konstrukcí vyplývající z konstrukčních zásad a možností provádění, materiálové vlastnosti jednotlivých tříd betonů nebo ocelí).

Je samozřejmě potřebné, aby byl definován jak způsob výpočtu ceny konstrukce, tak kritérium spolehlivosti.

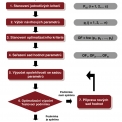
Proces optimalizace je pak možné popsat v následujících krocích:

1. Stanovení jednotlivých kritérií vycházejících z požadavků na konstrukci z hledisek bezpečnosti (únosnosti) a použitelnosti; počet těchto kritérií je označen c. Každému kritériu odpovídá jedna funkce spolehlivosti RF_i a návrhová pravděpodobnost P_d,i (i = 1, 2, ... c).
2. Výběr návrhových parametrů p_j (j = 1, 2, ... n), jejichž hodnoty budou v optimalizačním výpočtu měněny (například tloušťka stěny). Každému parametru odpovídá sada jeho hodnot (například přípustné hodnoty tloušťky stěny). Dále je možno stanovit vzájemné kombinace hodnot parametrů, které jsou v návrhu přípustné (pokud to nejsou všechny). Počet těchto kombinací (sad hodnot) je označen m.
3. Následuje stanovení optimalizačního kritéria (zpravidla náklady na konstrukci) a definice odpovídající optimalizační funkce OF, která je funkcí návrhových parametrů: OF = f (p₁, p₂, ... p_n). Cílem optimalizačního výpočtu je najít takovou sadu hodnot všech parametrů, při kterých jsou splněna všechna kritéria (krok 1) a při kterých zároveň hodnota optimalizační funkce dosahuje extrému (v případě nákladů nejlépe minima).
4. Seřazení sad hodnot parametrů podle jim odpovídající hodnoty optimalizační funkce. Získá se posloupnost OF₁, OF₂, ... OF_m.
5. Výpočet spolehlivosti se sadou parametrů odpovídající OF_k (v prvním kroku je k = 1), kterým se stanoví hodnoty pravděpodobností poruchy P_f,i,k.
6. Pokud platí P_f,i,k ≤ P_d,i,k pro všechna kritéria (i = 1, 2, ... c), je optimalizační výpočet ukončen a k-tá sada parametrů představuje optimální návrh. Tato sada hodnot parametrů se někdy označuje jako návrhový bod (v n-rozměrném prostoru).
7. Pokud výše uvedená nerovnost neplatí alespoň pro jedno z kritérií, provede se spolehlivostní výpočet (krok 5) s následující sadou hodnot parametrů k + 1.

Software
Pro ověření popisovaných přístupů byl vytvořen účelový software [2]. Ten umožňuje provádět statické řešení rotačních skořepin a řešit úlohu výběru optimální varianty konstrukce. Cena konstrukce je zde definována jako násobek objemu materiálu, přičemž pro jednotlivé části konstrukce je možné definovat rozdílné ceny a tak zahrnout například vliv složitější montáže u specifických prvků (například výztuh). Tento postup není univerzální, avšak postačuje pro skupinu úloh zatím řešitelnou diskutovanou metodikou.

Software umožňuje provádět optimalizaci s využitím jak normového posudku na vznik trhlin (s využitím zásad uvedených v [8]), tak s využitím pravděpodobnostního přístupu například podle principů metody SBRA [4] založené na simulační technice Monte Carlo. Problém vyšší výpočetní náročnosti při použití simulačního přístupu je možné podstatně omezit využitím paralelního provádění výpočtů na moderních počítačích, který je implementován v používaném simulačním jádru [1]. Výhledově se plánuje zrychlení výpočtů i pomocí dalších technik [3].

Příklad
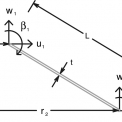
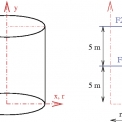
Použití popisovaného optimalizačního algoritmu může být ukázáno na příkladu rotační skořepiny zatížené dvojicí náhodně proměnných rotačně-symetrických silových zatížení (na obrázku 4 jsou označeny jako F1 a F2). Dalším náhodným parametrem byla pevnost betonu v tahu. Cílem optimalizace bylo najít vhodnou tloušťku stěny rotační skořepiny. Uvažovány byly tloušťky 0,1 m, 0,2 m, 0,3 m, 0,4 m, 0,5 m, přičemž se připouštělo, že každý z úseků skořepiny o výšce 5 m může mít jinou tloušťku.

Sestavený konečně-prvkový model obsahoval celkem 20 konečných prvků.

Algoritmus vedl na 25 možných variant (kombinací tloušťek skořepiny), přičemž jako optimální (tedy varianta s nejnižší cenou, která ještě vyhovuje podmínce spolehlivosti), byla v osmém kroku výpočtu vyhodnocena varianta s tloušťkou 0,3 m po celé výšce.

Úloha byla řešena na běžném notebooku (s frekvencí procesoru 2,4 GHz) a doba výpočtu byla v řádu desítek minut, přičemž v každém z provedených kroků se provádělo 1 000 000 konečně-prvkových výpočtů.

Závěr
Představený přístup je jednou z možných alternativ řešení problematiky optimalizace tvaru stavebních konstrukcí. Jeho výhodou je vysoká míra automatizace řešení a relativní jednoduchost a průhlednost použitých postupů. Určitou nevýhodou je vyšší výpočetní náročnost (zejména v úlohách, kdy se při ověřování spolehlivosti využívá simulačních metod), nicméně současná výpočetní technika již poskytuje dostatečné nástroje k dosažení přijatelných výpočetních časů. Uvedená vzorová realizace je zatím omezena na poměrně úzkou skupinu úloh, avšak stejným způsobem je možné postupovat i u dalších typů konstrukcí, což bude předmětem dalších prací.

Projekt byl realizován za finanční podpory ze státních prostředků České republiky prostřednictvím Studentské grantové soutěže v rámci specifického výzkumu na Vysoké škole báňské – Technické univerzitě Ostrava. Registrační číslo projektu je SP/2010151.

LITERATURA:
[1] Brozovsky et al. Monte software http://fast10.vsb.cz/brozovsky/monte (29. 9. 2010)
[2] Brozovsky et al. Software OPTIMIST http://fast10.vsb.cz/brozovsky/optimist (7. 10. 2010)
[3] Konečný, P. Vliv počtu náhodně proměnných na přesnost odhadu pravděpodobnosti poruchy metodou Monte Carlo. Sborník vědeckých prací VŠB – TUO, řada stavební, 2009, s. 173 –180, ISSN 1213-1962
[4] Marek, P., Gustar, M., Anagnos, T. Simulation-Based Reliability Assesment for Structural Engineers, Boca Raton, Florida, CRC Press, 1995, ISBN 0849382866
[5] Marek , Guštar et al. Simulation Based Reliability Assessment, http://sbra-anthill.com (12. 4. 2007)
[6] Phoon, K. K., S. T. Quek, S., T., Huang, H. Simulation of non-Gaussian processes using fractile correlation. Probabilistic Engineering Mechanics, Volume 19, 4, 2004, p. 287–292
[7] Schneider, P., Vykutil, J. Aplikovaná metoda konečných prvků, Lineární elastická analýza rotačních skořepinových konstrukcí. Brno: VUT v Brně, 1986, ISBN 80-214-0961-4
[8] Sekanina, D. Interakce předpjatých konstrukcí v kontaktu X s podložím, disertační práce, VŠB-TU Ostrava, Ostrava, 2010
[9] Zienkiewicz, O.C, Taylor, R. L., Zhu, J. Z. Finite Element Method, Its Basis and Fundamentals. Butterworth-Heinemann, Burlinghton, 2006
[10] JCSS: Probabilistic model code. JCSS working materials, http://www.jcss.ethz.ch/
[11] ISO 2394 General principles on reliability for structures, ISO, 1998

Approach to Computational Optimization of Axisymmetric Shells
The building structure has to be always designed not only reliably but also economically. Whereas the reliability and the efficiency assessment of the designed structure are possibly carried out by the relatively unambiguously defined procedures, the preparation and the finding of the optimal structure’ alternate of the structure is a task less exact and can be very elaborate. The submitted article deals with one of the possible approaches.

Autoři

• Ing. Sucharda Oldřich
• Ing. Valihrach Jakub
• Doc. Ing. Brožovský Jiří Ph.D.