Osová sila a ohyb prúta

1. ÚVOD
Pri priamom prúte osová sila neovplyvňuje priebeh ohybových momentov. To ale neznamená, že osová sila nemôže ovplyvniť ohybovú tuhosť prúta. V moderných konštrukciách sa stretávame s konštrukčným prvkom, kde sklenené tabule sú podoprené napnutými lanami. Aby sme boli schopní tento problém analyzovať je nutné použiť geometricky nelineárnu analýzu.

2. GEOMETRICKY NELINEÁRNA ANALÝZA PRÚTA
Na obr. 1 je rozkreslená deformácia diferenciálneho elementu strednice prúta. Pri bežnom riešení prútov uvažujeme pomerné predĺženie prúta pomerom medzi priemetom deformovaného elementu a pôvodnou dĺžkou, čo vedie na vzťah

   (1)

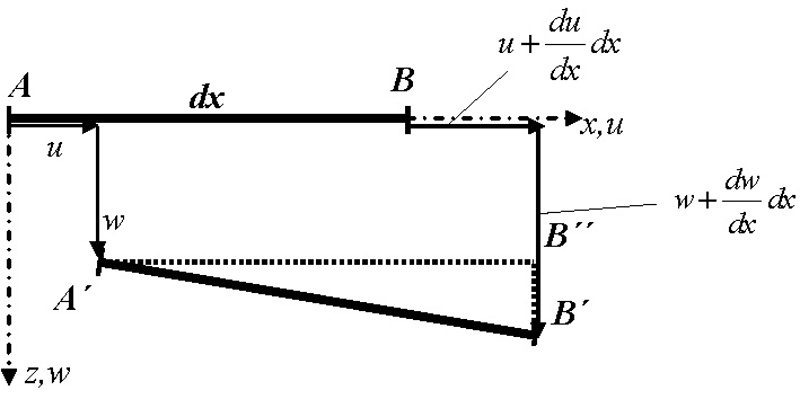
Obr. 1 – Deformácie diferenciálneho elementu strednice prúta

Ak vypíšeme pomerné predĺženie elementu v deformovanom stave postupne dostávame

   (2)

Použijeme Pytagorovu vetu a odmocninu rozpíšeme do binomického radu, z ktorého zoberieme iba prvý a druhý člen. V konečnom dôsledku dostávame výraz pre pomerné predĺženie

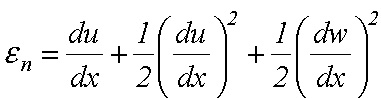   (3)

Keďže premiestnenia v smere prúta zvyknú byť výrazne menšie ako premiestnenia kolmo na prút (u << w), tak môžeme zjednodušiť

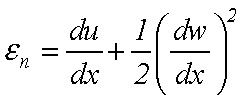   (4)

Získaný výraz už nie je lineárny. Z binomického rozvoja sme akceptovali iba prvý a druhý člen a podľa toho nazývame túto teóriu i teóriou druhého rádu.

Pre ďalšie riešenia budeme uvažovať lineárne pružný materiál

σ = E(ε −ε₀ ) (5)

kde E je modul pružnosti a indexom „0“ sme označili počiatočné deformácie.

Vypíšeme celkovú potenciálnu energiu. Pre ďalšie riešenia budeme využívať Ritzovou variačnú metódu. Takto postavená úloha, v dôsledku uvažovania druhej mocniny v pomernom predĺžení, v obecnom prípade vedie na systém kubických algebrických rovníc. V príklade priameho prúta sa kubické členy vzájomne eliminujú.

3. PRÚT NAMÁHANÝ OSOVOU SILOU A PRIEČNYM ZAŤAŽENÍM
Na obr. 2 sú ukázané dva príklady namáhania prúta, ktorým budeme venovať pozornosť.

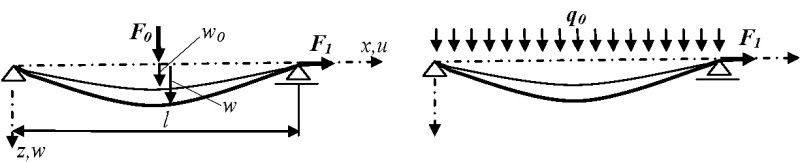
Obr. 2 – Prút namáhaný osovou silou a priečnym zaťažením

Uvažujeme prút so začiatočným zakrivením. Ako priečne zaťaženia budeme uvažovať dva príklady – zaťaženia sústredenou silou v strede a rovnomerné zaťaženie po celej dĺžke nosníka.

Ako už bolo spomenuté použijeme Ritzovu variačnú metódu s uvažovaním nasledovných základných variačných funkcií

   (6)

Detaily odvodenia nájde čitateľ v prácach [6,7,8]. Po úpravách úloha vedie na rovnicu

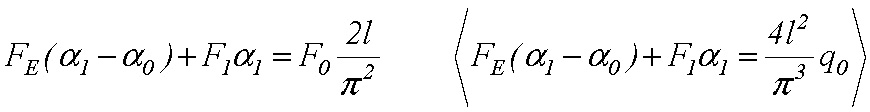   (7)

je 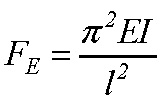 Eulerova kritická sila, EI – ohybová tuhosť prúta, l – rozpätie prúta.

Rovnica v zátvorke  platí pre príklad s rovnomerným zaťažením.

Realizujme kontrolu pre príklad priameho prúta (α₀ = 0 )a s nulovou osovou silou. Pre priehyb v strede dostávame

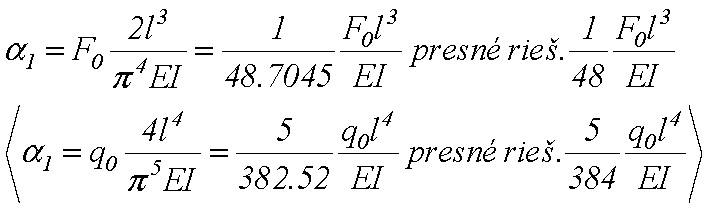   (8)

Vidíme, že sme nedostali presný výsledok. Je to dôsledok toho, že sme uvažovali sínus ako priehybovú funkciu. Rozdiely sú ale iba 1,5 % pre silu a 0,64 % pre rovnomerné zaťaženie.

Ďalšiu jednoduchú kontrolu urobíme pre príklad pôsobenia tlakovej sily a bez uvažovania priečneho zaťaženia. Potom dostávame známy výsledok pre vzper prúta so začiatočným zakrivením

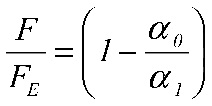  , kde    (9)

4. PRÚT S MALOU OHYBOVOU TUHOSŤOU NAMÁHANÝ ŤAHOVOU OSOVOU SILOU
Extrémnym príkladom je prút namáhaný ťahovou osovou silou a pritom tento prút má veľmi malú ohybovú tuhosť. Napríklad oceľové lano. V takomto prípade môžeme uvažovať že Eulerova kritická sila je rovná nule (F_E = 0 ) . Rovnica (7) sa zjednoduší na tvar

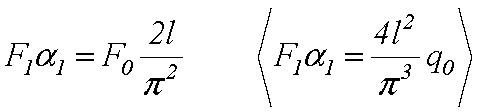   (10)

Venujme najprv pozornosť príkladu s priečnym zaťažením sústredenou silou. Zaujíma nás veľkosť osovej sily (sily v lane)

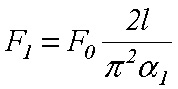   (11)

Tuhosť na priehyb limitujeme podielom voči rozpätiu  , kde zvykneme uvažovať v hodnotách n = 250-800. Dosadením do rovnice (11) dostávame

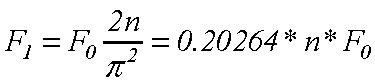   (12)

Pre ilustráciu uvažujme F₀ = 1000 N, n = 500 . Dostávame silu v lane F₁ = 101321N .

Veľkou zaujímavosťou je skutočnosť, že do tohto vzťahu nevstupuje rozpätie nosníka ani jeho tuhosť. Pre porovnanie si ukážeme závislosti medzi silami na napnutom lane obr. 3.

Obr. 3 – Sily na napnutom lane

Z podmienky rovnováhy vertikálnych síl dostávame

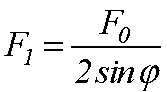   (13)

Jedná sa o malý uhol „ϕ“, pre ktorý môžeme urobiť úpravu

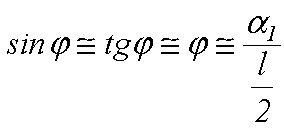   (14)

Dosadením dostávame výsledok

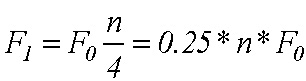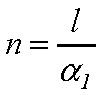 ,    (15)

Rozdiel medzi výsledkami rovn. (12) a rovn. (15) nie je veľký. Pri rovn. (12) sme uvažovali priehybovú funkciu v tvare sínus a pri rovn. (15) je to lomená čiara. Veľkou zaujímavosťou je skutočnosť, že do týchto vzťahov nevstupuje rozpätie nosníka ani jeho tuhosť. Pre priečne rovnomerné zaťaženie analogickými úpravami, aké sme urobili pre rovn. (12), dostávame vzťah

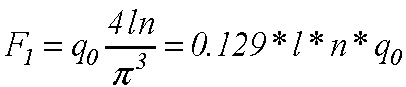   (16)

Uvažujme príklad l = 5.0m, q₀ = 200N / m, n = 500. Sila v lane je F₁ =64503N .
Príklad rovnomerného zaťaženia a lana vedie na úlohu visutého lana resp. reťazovky.

5. STABILITA A KMITANIE PRÚTA
Ak osová sila je tlaková, tak prechádzame do problémov stability. Zaujímavý je problém kombinácie stability a kmitania prúta. Ak uvažujeme lineárnu dynamiku resp. úloha je geometricky lineárna, tak problém voľného kmitania vedie na rovnicu

   (17)

kde K_L je tuhostná matica, ω – vlastná kruhová frekvencia , K_M – matica hmotnosti.

V príkladoch stability pre mnohé úlohy je postačujúce použiť teóriu lineárnej stability. Lineárna stabilita predpokladá, že osové sily v prúte resp. membránové sily v tenkostennej konštrukcii nie sú závislé na priečnej deformácii. Takto postavená úloha umožňuje určiť kritické sily resp. kritické napätia a tvary vybočenia. Ak predpoklady lineárnej stability uvažujeme i v úlohe kmitania konštrukcie, tak rovnica (17) sa zmení na

   (18)

kde K_G je tzv. geometrická matica, λ – násobiteľ kritického zaťaženia.

Ak ale uvažujeme geometricky nelineárnu analýzu bez linearizujúcich zjednodušení, tak úloha vedie na systém kubických algebrických rovníc. Jedným z vhodných postupov je výpočtový model vychádzajúci z prírastkovej formulácie, z ktorého vyústi prírastkový postup i Newton-Raphsonova iterácia. Ak takto postavenú úlohu rozšírime do dynamiky, tak problém vlastného kmitania vedie na rovnicu

   (19)

kde K_INC je prírastková tuhostná matica.

Prírastková tuhostná matica zahŕňa v sebe začiatočné deformácie, hladinu zaťaženia i deformácie sústavy zodpovedajúce danému zaťaženiu. Detailné vysvetlenie teoreticko-numerického pozadia daného problému je spracované v prácach citovaných v závere. Na tomto mieste uvedieme iba niekoľko výsledkov.

Kmitanie a vzper prúta
Základným príkladom pre kombináciu stability a kmitania je prút kĺbovo podopretý na koncoch zaťažený osovou silou. Už tento jednoduchý príklad upozorní na zložitosť daného problému. V mieste pôsobenia sily musíme uvažovať posuvnú podperu. Ak takýto model uvažujeme i pre príklad kmitania prúta, tak pri kritickej sile dostávame nulovú frekvenciu. Tento výsledok ale odporuje realite. Napríklad banský predák keď kontroluje výdrevu, tak preťaženosť podperných stĺpov je sprevádzaná vysokými frekvenciami. Aby sme dostali výsledok zodpovedajúci realite, musíme v procese kmitania prúta uvažovať neposuvnú podperu. Výsledok je dokumentovaný na obrázku 4. Výsledky sú spracované do bezrozmerných veličín, kde

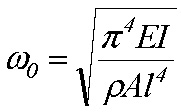 je vlastná kruhová frekvencia nosníka, ρ – objemová hmotnosť, A – prierezová plocha, r – polomer zotrvačnosti prierezu.

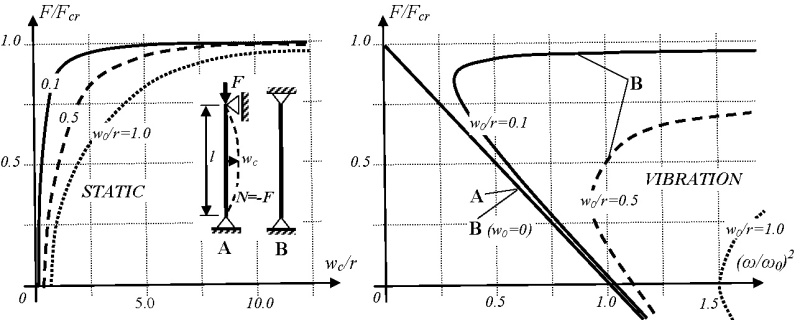
Obr. 4 – Stabilita a kmitanie prúta so začiatočnou deformáciou

Vplyv tvaru počiatočnej deformácie na kmitanie prúta
V prípade ideálneho prúta je tvar kmitania zhodný s tvarom vybočenia. To má za následok, že závislosť medzi zaťažením a štvorcom vlastnej kruhovej frekvencie je priamka. Pri úlohe statiky ako najnepriaznivejší tvar začiatočnej deformácie je tvar zhodný s tvarom vybočenia zodpovedajúci najnižšej kritickej sile („tvar 1“). Obr. 5 poukazuje na zaujímavosť vznikajúci pri kmitaní prúta. Aj keď prút má tvar začiatočnej deformácie blízky „druhému tvaru vybočenia“, prút kmitá v prvom tvare.

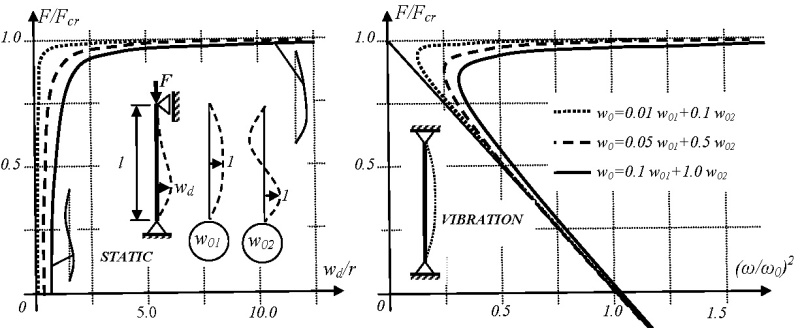
Obr. 5 – Stabilita a kmitanie prúta so začiatočnou deformáciou v druhom tvare vybočenia

Experimentálne merania
Vo všeobecnosti platí, že dobrý výskum teórie konštrukcií je kombinácia teoretického, numerického a experimentálneho výskumu. Už úvodné príklady pre kombináciu stability a kmitania ukázali prekvapivé výsledky. Pre overenie týchto výsledkov pripravili autori špeciálne zariadenie pre experimentálne merania v laboratóriu. Schéma zariadenia je ukázaná na obrázku 6. Obrázok 7 ukazuje skúšku spojitého nosníka so sústredenou silou v strede. Pripraveným zariadením bolo realizovaných množstvo meraní. Niektoré výsledky si dovolíme ukázať.

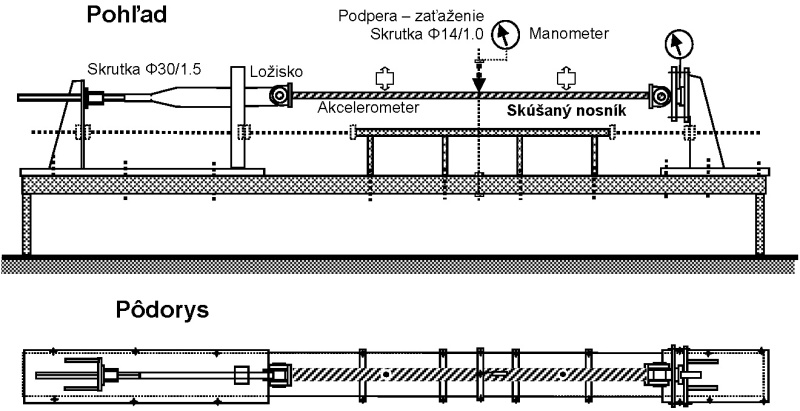
Obr. 6 – Schéma zariadenia pre skúšku stability a kmitania prútov

Obr. 7 – Pohľad na skúšku nosníka

Sily sú generované skrutkami s malým stúpaním závitu. Znamená to, že skúška bola realizovaná pri tzv. tuhom režime. Sily boli merané manometrami. Deformácie boli merané kombináciou mechanických a bezkontaktných priehybomerov. Pri meraní frekvencie boli mechanické priehybomery odložené. Vplyv koncových podperných ložísk na vlastnú kruhovú frekvenciu je ukázaný na obr. 8.

Obr. 8 – Vplyv koncových podperných ložísk na maticu hmotnosti

Matica hmotnosti s vplyvom koncových podporných ložísk je

   (20)

Uvažuje sa udávanie všetkých vstupov v rozmeroch [kg, m, s]. Pri realizovaných experimentoch tento vplyv bol nižší ako 1,5 %.

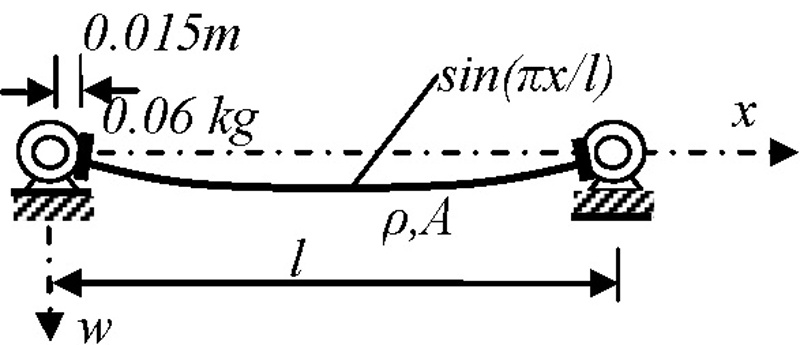
Tenkostenný oceľový profil Jäckl 30/15/1.5 mm
Oceľ má stály modul pružnosti i objemovú hmotnosť (E = 210 000 MPa, ρ = 9850 kg/m³). Kombináciou merania a váženia bolo možné spresniť dimenzie skúšaného Jäcklového profilu, kde otvorenou otázkou je hrúbka steny. Skúšaný bol nasledovný profil:

Jäckl 29.9 / 14.8 / 1.53, A = 121.4 mm², I = 4286.0 mm⁴, r = 5.94 mm, l = 1450 mm
E = 210000 MPa, μ = 7850 kg / m³, F_cr = 4225.1 N, ω₀ = 144.2 s^-1

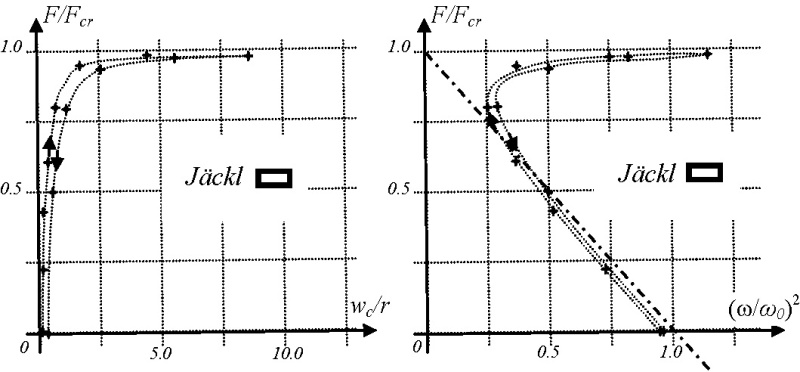
Obr. 9 – Skúška stability a kmitania tenkostenného oceľového profilu

Drevený nosník
Premeraním a odvážením vieme presne určiť objemovú hmotnosť dreva. Otvorenou otázkou je určenie modulu pružnosti. Autori si pomohli nasledovným postupom. Pri skúške stability sa dalo postrehnúť stav, kedy rastie deformácia prúta pri minimálnom raste sily. Túto silu môžeme považovať ako Eulerovu kritickú silu. Keďže poznáme rozmery prierezu i dĺžku nosníka, tak z Eulerovej sily vieme určiť modul pružnosti. Tento postup ukazuje na možnosť využitia pripraveného zariadenia pre nedeštruktívnu metódu určovanie modulu pružnosti. Získaný výsledok pre dva drevené nosníky je spracovaný na obr. 10.

Drevený nosník 47 / 47 mm, A = 2209 mm², I = 406640 mm⁴, r = 13.57 mm, l = 2040 mm
E = 10200 MPa, ρ = 472 kg / m³, F_cr = 9836.7 N, ω₀ = 147.3 s^-1
Drevený nosník 42 / 32 mm, A = 1344 mm², I = 114888 mm⁴, r = 9.24 mm, l = 1650 mm
E = 9750 MPa, ρ = 454 kg / m³, F_cr = 4060.8 N, ω₀ = 1154.9 s^-1

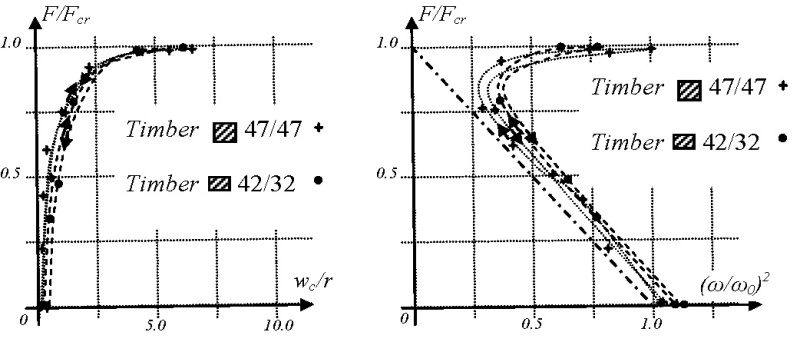
Obr. 10 – Skúška stability a kmitania drevených nosníkov

Prezentované výsledky jasne potvrdzujú skutočnosť, že pri približovaní sa zaťažujúcej sily ku kritickej sile, rastie vlastná kruhová frekvencia do vysokých hodnôt.

Spojitý nosník
Obr. 11 udáva rozmery skúšaného spojitého nosníka. Skúška bola realizovaná na dva kroky. (Obr. 12). Získané výsledky sú spracované na obrázkoch 13 a 14. Vidíme, že vďaka podpere v strede osová sila mohla prekročiť kritickú silu pre prostý nosník.

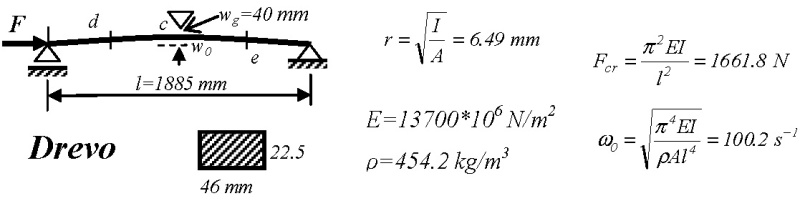
Obr. 11 – Rozmery skúšaného dreveného spojitého nosníka

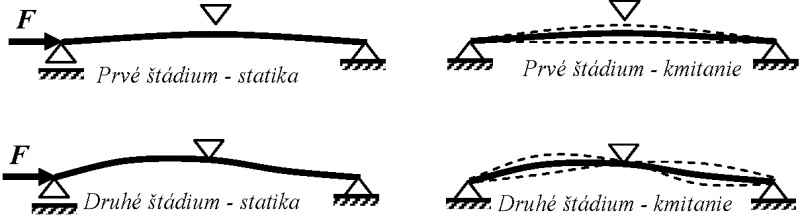
Obr. 12 – Dve štádia pôsobenia spojitého nosníka

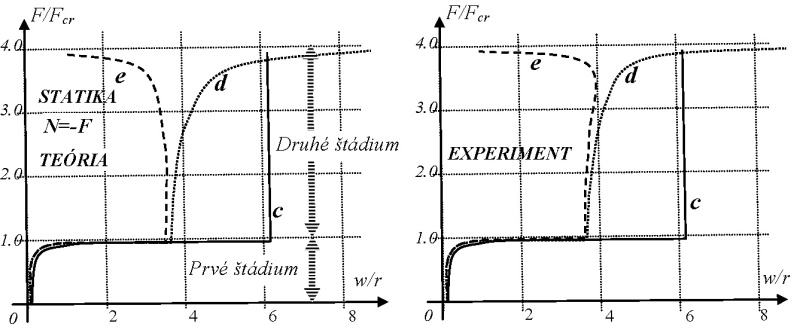
Obr. 13 – Statika pôsobenia spojitého nosníka

6. ZÁVER
Autori článku sa venujú problémom stability konštrukcií. Riešiť úlohy stability si vyžaduje zvládnuť riešenie geometricky nelineárnych úloh. Stačilo zmeniť tlakovú silu za ťahovú, zachovať plne geometricky nelineárnu analýzu a dostavil sa zaujímavý výsledok pre určenie vplyvu osovej sily na ohybovú tuhosť prúta.

Postavenie kombinácie stability a kmitania umožňuje určiť frekvenciu sústavy s uvážením hladiny zaťaženia ako i vplyv veľkosti a tvaru počiatočnej deformácie. Porovnávanie teoreticko-numericky vyhodnotenej frekvencie s frekvenciou nameranou na reálnej konštrukcii je základom pre skupinu nedeštruktívnych metód identifikácie vlastností resp. kvality konštrukcií. Jedna z možností použitia prezentovanej teórie je ukázaná na obr. 15. Pri mohutných objektoch nie sme schopní realizovať rozkmitanie objektu ako celku. Dokážeme ale rozkmitať dielčie časti. Analyzovanie kmitania stĺpov si vyžaduje použiť prezentovanú teóriu s geometricky nelineárnym pozadím.

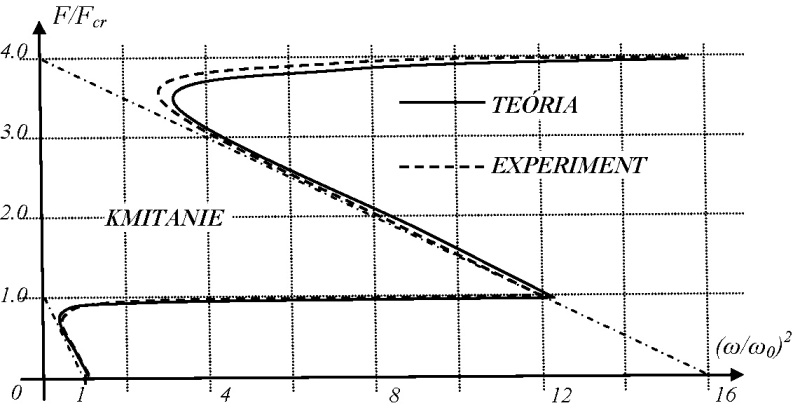
Obr. 14 – Závislosť štvorca kruhovej frekvencie na zaťažení

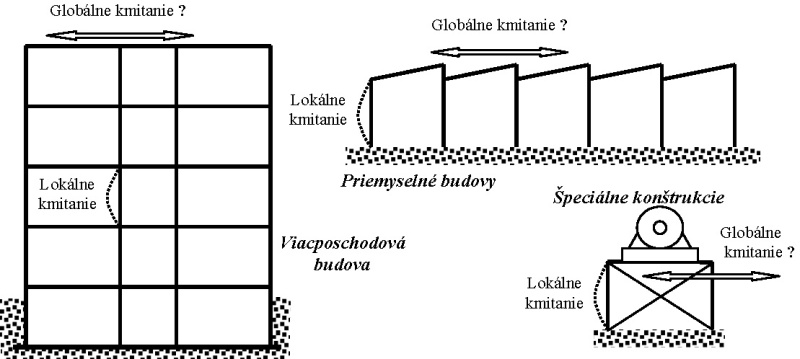
Obr. 15 – Schéma pre nedeštruktívnu metódu identifikácie vlastností konštrukcie

Predložený článok bol spracovaný s podporou Slovenskej vedeckej grantovej agentúry, grant č. 1/0272/15.

LITERATÚRA:
[1] Bažant Z. P., Cedolin, L.: Stability of Structures: Elastic, Inelastic, Fracture and Damage Theories. Oxford University Press, New York, Oxford, 1991.
[2] Bolotin V. V.: Dinamičeskaja ustojčivosť uprugich system. CITL. Moskva, 1956 (Anglický preklad: Holden Day. San Francisco, 1994.)
[3] Burgreen D.: Free Vibration of Pined Column with Constant Distance Between Pin-ends. J. Appl. Mechan., 18, 1951. 135–139.
[4] Kolakowski K., Kowal-Michalska K.: Statics, Dynamics and Stability of Structures, Vol. 2. Statics, Dynamics and Stabilty of Structural Elements
and Systems. Quick-Druck, Lodz, 2012.
[5] Krolak M., Mania R. J.: Statics, Dynamics and Stability of Structures, Vol. 1. Stability of Thin-Walled Plate Structures. Quick-Druck, Lodz, 2011.
[6] Ravinger J.: Vibration of an Imperfect Thin-walled Panel. Part 1: Theory and Illustrative Examples. Part 2: Numerical Results and Experiment.
Thin-Walled Structures, 19, 1994, 1-36.
[7] Ravinger, J., Kleiman, P.: Natural Vibration of Imperfect Columns and Frames. Building Research Journal, 2002, Vol. 50, No. 1, 49-68.
[8] Ravinger J.: Stability & Vibration. STU Bratislava, 2012
[9] Volmir A.S.: Nelinejnaja dinamika plastinok i oboloček. Nauka. Moskva. 1972.

Axial force and bending of beam
Geometric nonlinear theory had to be used for an investigation of the effect of axial force to bending stiffness. Tension force increases bending stiffness. In the case of the beam with very small bending stiffness (e.g. the rope) the problem is reduced and we are able to evaluate axial force that is necessary to reach defined bending stiffness. Assuming compression force we enter the stability problems. Elastic critical load is limit for compression force. This rule does not valid in the case of having initial deformation opposite to action of transverse force. We can use measuring of frequencies for the identification of axial forces. In the case of compression forces we have problem of stability and vibration.

Autoři

• Dr.h.c. prof. Ing. Ravinger Ján DrSc.
• Ing. Šnirc Luboš