Odolnosť nosníkov žeriavových dráh podľa eurokódov
Rubrika: Zajímavosti
METÓDY POSÚDENIA NOSNÍKOV ŽERIAVOVÝCH DRÁH
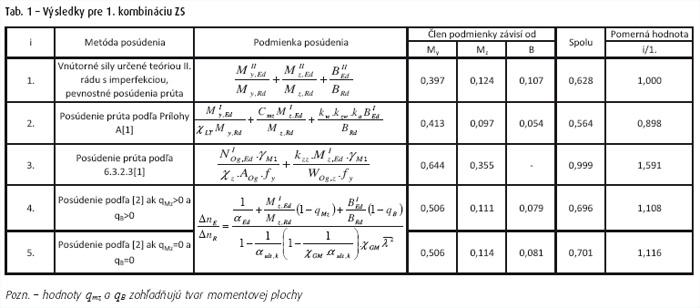
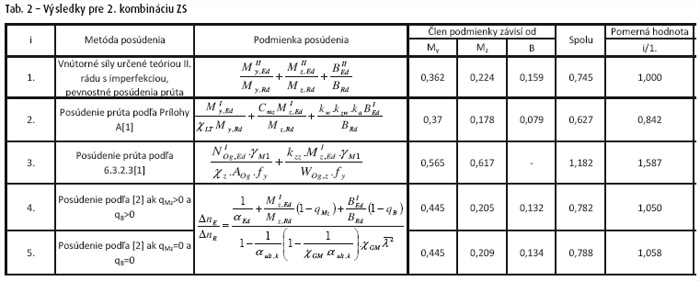
Podľa platnej normy pre navrhovanie nosníkov žeriavových dráh [1], je možné pri zisťovaní odolnosti použiť tri metódy. Dve metódy pracujú s vnútornými silami získanými teóriou prvého rádu bez imprefekcií, potom sa nosník žeriavovej dráhy posúdi ako náhradný prút. Tretia metóda spočíva v pevnostnom posúdení prierezu, kde vnútorné sily sú určené teóriou druhého rádu s imperfekciami. Okrem týchto postupov sú v článku uvedené výsledky pre postup publikovaný v dizertačnej práci Naumesa [2].
Posúdenie nosníka podľa 6.3.2.3 [1]
Podľa tejto časti sa odolnosť nosníka žeriavovej dráhy overí tak, že sa posúdi tlačená pásnica plus jedna pätina steny ako tlačený prút na rovinný vzper (vybočenie z roviny nosníka). Takýto prút sa má posúdiť na osovú tlakovú silu rovnú ohybovému momentu od zvislého zaťaženia, vydelenému vzdialenosťou ťažísk pásnic. Vziať do úvahy sa má tiež ohybový moment od priečneho vodorovného zaťaženia a účinky krútenia.

Posúdenie nosníka podľa Prílohy A[1]
Táto metóda sa môže použiť pre posúdenie únosnosti pri klopení prostého NŽD konštantného prierezu so zvislým zaťažením a priečnym vodorovným zaťažením pôsobiacim mimo stredu šmyku. Zaťaženie sa má vyjadriť ako zvislé a vodorovné sily pôsobiace v strede šmyku plus krútiaci moment Tw od viazaného krútenia. Prúty namáhané kombináciou ohybu a krútenia majú splniť nasledujúcu podmienku:

Redukčný súčiniteľ klopenia χLT sa určí podľa 6.3.2.3 [3] pre valcované alebo ekvivalentné zvárané prierezy so zhodnými pásnicami alebo rôznymi pásnicami, kde b je šírka tlačenej pásnice, za predpokladu, že:
Iz,t /Iz,c ≥ 0,2
Kde Iz,c a Iz,t sú kvadratické momenty plochy k osi z-z tlačenej a ťahanej pásnice.
Hodnoty odolností prierezov sa určia podľa časti 6.2 [3]
- Pri prierezoch triedy 1 a 2 možno využiť plastickú odolnosť,
- Pri prierezoch triedy 3 a 4 elastická odolnosť.
Posúdenie prierezu pre vnútorné sily určené teóriou II. rádu s imerfekciami
V tejto metóde sa nosník posudzuje v najviac namáhanom priereze a vplyv všetkých imperfekcií je nahradený geometrickou imperfkeciou v tvare sínusoidy (paraboly). Hodnoty imperfekcií sa určia ako pre ohýbaný nosník.
V súčasnosti sa hodnota takejto imperfekcie rovná polovičnej hodnote pre vybočenie kolmo na rovinu väčšej tuhosti. Výpočet vnútorných síl je teóriou druhého rádu.

PRÍKLADY POSÚDENIA NOSNÍKOV ŽERIAVOVÝCH DRÁH
Posúdenie jednopoľového nosníka s dvojososymetrickým prierezom
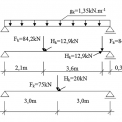
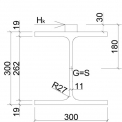
Proste uložený NŽD o dĺžke 6 m z ocele S 235. Nosník je z profilu HEB 300. Zaťažený podľa obr. 1. Zvislé zaťaženie pôsobí v strede šmyku (podľa 6.3.2.2 (1) [1]). Vodorovné zaťaženie pôsobí na temene koľajnice (podľa obr. 2).
Zaťažovacie stavy:
- Zaťažovací stav predstavuje vlastná tiaž [(+ tiaž koľajnice) obr. 1a].
- Zaťažovací stav (obr. 1b) sú účinky kolesových tlakov podľa zaťažovacej skupiny 1
- Zaťažovací stav (obr. 1c) sú kolesové tlaky podľa zaťažovacej skupiny 5.
Hodnota krútiaceho momentu sa určí z obr. 2 keď vodorovnú silu presunieme do stredu šmyku a prídavný krútiaci moment sa následne určí ako Tk = r . Hk
pre 2. zaťažovací stav je Tk = 0,18 m . 12,9 kN = 2,322 kNm
pre 3. zaťažovací stav je Tk = 0,18 m . 20,0 kN = 3,600 kNm
Kombinácie zaťažovacích stavov
- Kombinácia ZS – Maximálny moment My 1,35 (ZS1 + ZS2)
- Kombinácia ZS – Maximálny moment Mz 1,35 (ZS1 + ZS3)
Lokálna imperfekcia bola určená pre vzpernú krivku „c“ a elastickú analýzu
vel = L / 400 = 6 000 mm / 400 = 15 mm
Posúdenie jednopoľového nosníka s jednososymetrickým prierezom
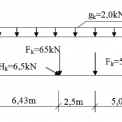
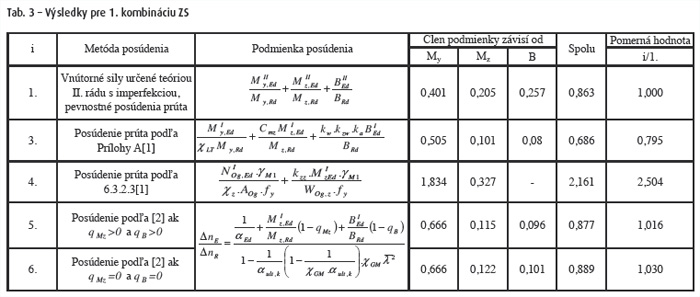
Dĺžka nosníka 14 m, Oceľ S235, Proste uložený NŽD o dĺžke 14 m z ocele S 235. Nosník je zo zváraného profilu podľa obr. 5. Zaťažený podľa obr. 4. Zvislé zaťaženie pôsobí v strede šmyku. Vodorovné zaťaženie pôsobí na temene koľajnice (podľa obr. 5).
Zaťažovacie stavy:
- Zaťažovací stav predstavuje vlastná tiaž (+ tiaž koľajnice) obr. 4a.
- Zaťažovací stav (obr. 4b) sú účinky kolesových tlakov podľa zaťažovacej skupiny 1
Hodnota krútiaceho momentu sa určí ako Tk = r . Hk
pre 2. zaťažovací stav je Tk = 0,299 m . 6,5 kN = 1,9435 kNm
Základné kombinácie zaťažovacích stavov
Kombinácia ZS – Maximálny moment 1,35 (ZS1 + ZS2)
Lokálna imperfekcia bola určená pre vzpernú krivku „c“ a elastickú analýzu
vel = L / 400 = 14 000 mm / 400 = 35 mm
ZÁVER
V článku sú uvedené a v skratke popísané metódy overenia odolnosti nosníkov žeriavových dráh. Z uvedených výsledkov vyplýva, že vzhľadom k vzťažnému prípadu (posúdenie prierezu pre vnútorné sily určené teóriou II. Rádu s imperfkeciami) sú najpresnejšie výsledky pre postup, ktorý publikoval Naumes vo svojej dizertačnej práci [2]. Metódy posúdenia náhradného prúta sú menej presné a pre metódu z Prílohy A [1] na strane nebezpečnej. Pre metódu podľa článku 6.3.2.3 [1] je možné povedať, že je na strane bezpečnej, je však veľmi konzervatívna. Nevýhodou metód podľa Prílohy A a článku 6.3.2.3 [1] je aj to, že ich nemožno aplikovať na spojité nosníky.
Recenzoval Tomáš Živner, Ing., PhD., Slovenská technická univerzita v Bratislave, Stavebná fakulta, Katedra kovovýcha drevených konštrukcií, odborný asistent.
LITERATURA:
[1] STN EN 1993-6: Navrhovanie oceľových konštrukcií Časť 6: Žeriavové dráhy. November 2009.
[2] Naumes, J.: Biegeknicken und Biegedrillknicken von Stäben und Stabsystemen auf einheitlicher Grundlage. Aachen 2010. ISBN 978-3-8322-8754-2
[3] STN EN 1993-1-1/NA: Navrhovanie oceľových konštrukcií Časť 1-1: Všeobecné pravidlá a pravidlá pre budovy/Národná príloha. December 2007.
Resistance Of Craneway Beams According To Eurocodes
The craneway beams represent demanding structures in terms of their operation. The craneway beams can be stressed by bending in two planes and a torsional moment. Under current standards for craneway beams, it is possible for such stressed structures to be designed according to three different methods. Although the usage of two methods out of three is limited to simply supported beams. The other method is the calculation of the theory of II. order on the structure with an imperfection. The article presents the calculations of the two craneway beams using the standard patterns of interaction as well as the method published by Dr. J. Naumes in his dissertation thesis.