Numerický model Z vaznic za požáru

• Foto

NUMERICKÝ MODEL VAZNICE
Cílem numerického modelu bylo co nejvěrněji simulovat požární zkoušku publikovanou již dříve v časopise Konstrukce [2]. Jednalo se o zkoušku vaznic průřezu Z, výšky 200 mm a tl. 1,5 mm. Tyto vaznice byly pnuty na rozpětí 6 m s jedním převislým koncem (mimo pec). Tím měl být zohledněn průběh vnitřních sil, jako je tomu u krajního pole spojitého nosníku. Na podpoře u převislého konce bylo využito rukávu tl. 2 mm, který zajišťuje spojitost vaznic. Zkouška byla provedena pro vaznice s i bez trapézového plechu uloženého na horní pásnici profilů. Numerický model je proveden pouze pro případ vaznice bez trapézového plechu, nicméně závěry jsou společné i pro případ vaznice stabilizované plechem.

K modelování byl použit software Abaqus a SAFIR založený na metodě konečných prvků. V první fázi byl vytvořen trojrozměrný model vaznice z deskostěnových prvků a později zjednodušující „inženýrský“ prutový model.

PROSTOROVÝ MKP MODEL VAZNICE VYUŽÍVAJÍCÍ DESKOSTĚNOVÝCH PRVKŮ
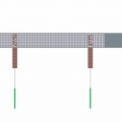
Prostorový model vaznice s využitím deskostěnových (shell) prvků byl vytvořen v programech SAFIR (zde prezentováno) a Abaqus. Použití dvou různých programů bylo důvodem pro další ověření jejich správnosti. Model v programu SAFIR je znázorněn na obr. 1.

V modelu byly modelovány botky, zjednodušeně i šroubový přípoj vaznice na botku. Převislý konec (mimo pec) byl rovněž v modelu uvažován s okrajovými podmínkami odpovídajícími experimentu. Překrytí rukávem nad jednou z podpor bylo v modelu zohledněno pouze zvýšením tl. stěny vaznice z 1,5 mm na 2 mm. Reziduální pnutí byla zanedbána. Geometrické imperfekce byly zohledněny na základě výrobních tolerancí dle doporučení pro MKP modely v EN 1993‑1‑5 [3]. Zatížení bylo modelováno spolu se závěsem (plochá pásová ocel), tj. ve shodě s jeho skutečným zavěšením při zkoušce.

Materiálové charakteristiky byly uvažovány charakteristickou hodnotou pro ocel S 350, přičemž redukční součinitele zohledňující vliv vysoké teploty byly převzaty z Francouzké národní přílohy EN 1993‑1‑2. Ta na rozdíl od základní části normy uvádí součinitele zvlášť i pro ocel za studena tvarovaných průřezů.

Teplota v prvku, resp. částí vystavených požáru byla vypočítána v programu Elefir‑EN na základě tepoty plynu uvažované již zmíněnou normovou křivkou ISO 834. Spočítaný průběh teploty se dobře shodoval s hodnotami naměřenými během zkoušky. V podstatě se jednalo o průměrnou teplotu v prvku.

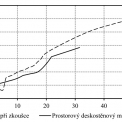
Model byl uvažován nejprve s teplotní roztažností. Stejně jako při experimentu došlo u tohoto modelu vlivem teplotní roztažnosti k vyvození osové síly a dosažení únosnosti prvku v tlaku s ohybem. Pro získání chování následně po vybočení pak byl použit model bez teplotní roztažnosti, který je zde prezentován. Ten nepostihuje věrně chování vaznice v počátku zahřívání (prvních cca 7 min). V další části, kdy již teplotní roztažnost nemá velký význam (jí vyvozená osová síla je uvolněna deformací v některých průřezech vaznice) je skutečné chování postihnuto poměrně věrně, viz obr. 2.

V modelu je patrný náhlý pokles ohybové tuhosti mezi cca 15 – 20 min požáru daný vyčerpáním ohybové únosnosti vaznice. Nicméně i nadále je vaznice schopna přenášet zatížení díky neposuvnému uložení v obou podporách, prut se ale chová jako tažené vlákno, nikoliv nosník. Deformovaný tvar po zkoušce a tvar deformace z modelu je pro vaznici a detail přípoje na patku zobrazen na obr. 3 a 4.

Jedním ze závěrů modelování je, že pomocí numerické simulace je možné postihnout chování vaznice při požáru, byť zde také zůstávají určitá omezení. Pokročilého modelu může být využito například i při plánování požárních zkoušek, které jsou finančně velmi nákladné. Pro běžný inženýrský návrh je ale použití podobného modelu
náročné na čas i softwarové vybavení.

PRUTOVÝ MKP MODEL VAZNICE
Jako inženýrsky přijatelná alternativa byl vytvořen prutový model vaznice. S ohledem na to, že vaznice během požáru rychle ztrácí svou ohybovou tuhost, byla pro průřez vaznice zvolena kruhová tyč, tedy průřez, u kterého je ohybová tuhost zanedbatelná. Plocha průřezu byla totožná s plochou Z vaznice v poli. Prut byl modelován na stejné rozpětí (6 m) a na obou koncích podepřen neposuvným kloubem.

Je samozřejmé, že model nemůže věrně postihnout počáteční fázi zkoušky (nosníkové chování). Na druhou stranu, po vyčerpání ohybové únosnosti (cca po 20 min) je zjednodušení reprezentované zanedbáním ohybové tuhosti prutu poměrně přesné.

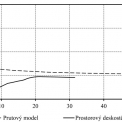
Pro návrh vaznice za požáru se jako klíčový jeví správný návrh přípoje vaznice na krajní podpoře. Účelem prutového modelu je co nejpřesněji stanovit vodorovnou sílu v tomto přípoji. Posouzení přípoje samotného, nebo stanovení ohybové únosnosti vaznice je s využitím EN 1993‑1‑3 [4] a 1993‑1‑2 [1] možné. Porovnání vypočtené vodorovné reakce v přípoji vaznice stanovené pomocí prostorového deskostěnového modelu a prutového modelu je na obr. 5.

ZÁVĚR
Článek na výsledcích numerického modelu názorně ukazuje chování tenkostěnných vaznic za požáru. Během nárůstu teploty je ve vaznici vlivem teplotní roztažnosti nejprve vyvozena osová síla. V důsledku toho pak vaznice může vybočit (celkový vzpěr), nebo dojde k deformaci v průřezech exponovaných při ohybu (uprostřed rozpětí, před místem zdvojení vaznice rukávem apod.). Tato síla zároveň nesmí překročit únosnost přípoje vaznice na botku. Proto musí být tento přípoj na vyvozenou reakci dimenzován. Zjednodušeně a konzervativně je možné přípoj navrhnout na únosnost vaznice v tlaku.

V další fázi je vaznice stále schopna přenášet ohybové zatížení. Ohybovou únosnost prutu za požáru je možné stanovit pomocí EN 1993‑1‑2. Po jejím vyčerpání je možné uvažovat prut jako tažené vlákno (rovnice lana, MKP model prutu bez ohybové tuhosti) a stanovit reakci v podpoře. I když tato reakce bude jistě výrazně nižší, než je vodorovná reakce v počáteční fázi požáru (osová síla od teplotní roztažnosti), bude s ohledem na redukci únosnosti přípoje vlivem vysoké teploty ve většině případů pro správný návrh rozhodující. Během popisované požární zkoušky k jeho porušení nedošlo, neboť bylo místo přípoje chráněno tepelnou izolací.

Samozřejmě je nutné, aby vodorovná síla z reakce vaznice byla dále přenesena ztužujícím systémem a dalšími částmi konstrukce. Tento návrh je specifickým tím, že nestačí posoudit pouze stávající prvek na požární odolnost, ale je nutné zohlednit změnu statického schématu samotné vaznice a s tím spojené důsledky pro vlastní konstrukci objektu. Tyto souvislosti také rozhodují o tom, zda vaznice může stabilizovat primární nosnou konstrukci apod.

Článek vznikl s podporou Studentské grantové soutěže ČVUT v Praze SGS 1611331A134.

LITERATURA:
[1] ČSN EN 1993‑1‑2 Eurokód 3: Navrhování ocelových konstrukcí – Část 1–2: Obecná pravidla – Navrhování na účinky požáru, ČNI, 2006.
[2] Schwarz, I., Jandera, M. Zkouška chování tenkostěnných Z vaznic za požáru, Konstrukce, č. 1, 2015, s. 40–43.
[3] ČSN EN 1993‑1‑5 Eurokód 3: Navrhování ocelových konstrukcí – Část 1–5: Boulení stěn, ČNI, 2008.
[4] ČSN EN 1993‑1‑3 Eurokód 3: Navrhování ocelových konstrukcí – Část 1–3: Obecná pravidla – Doplňující pravidla pro za studena tvarované prvky a plošné profily, ČNI, 2008.

Numerical Model of Z‑Purlins during a Fire
When designing cold‑formed steel elements in the structures, it is often important to take into account their load capacity in case of a fire. If the profiles are not protected against the fire, it is usually difficult to prove even a 15‑minute fire resistance by calculation. This is further complicated by the fact that the design standard ČSN EN 1993‑1‑2 [1] limits the maximum temperature of the cross‑section of the class 4 by the value of 350 °C. Another possibility of the verification of resistance can be an expensive fire test. Introduced article discusses the behaviour of purlins under the fire based on numerical model, which builds on an earlier carried out fire test [2]. Finally, there is also suggested a simplified procedure for the assessment of purlins under the fire.

Autoři

• Ing. Schwarz Ivo
• Ing. Jandera Michal Ph.D.
• MSc. Arrais Flávio Alexandre Matias
• Ing. Slatinka Martin