Numerická analýza vlivu parametrů MKP modelu podzákladí na modální charakteristiky systému podzákladí-konstrukce

Z uvedeného vyplývá nutnost řešit odezvu na dynamické zatížení v interakci s podzákladím. V dynamice nelze nahradit podzákladí například Winkler–Pasternakovým modelem podloží s konstantami C1 a C2, ani efektivním modelem podloží (Kolář, Němec) s celou řadou dalších konstant (liniovými a rohovými pružinami). Toto zjednodušení by bylo přípustné pouze ve statické analýze konstrukce.

Modelování zeminového bloku metodou konečných prvků (MKP) s sebou však nepřináší pouze výhody, ale i problémy. Samotné vytvoření modelu podzákladí je v programovém systému ANSYS relativně jednoduché, avšak problém nastává například ve zvolení velikosti modelu podzákladí, ve volbě jeho tvaru, ve způsobu diskretizace a ve volbě okrajových podmínek. Analýza některých těchto parametrů je hlavním cílem této studie. Prostorový výpočtový model s podzákladím také klade vyšší nároky na výpočetní čas a na objem dat. Z toho důvodu je výpočtový čas sledován jako další parametr (všechny analýzy jsou provedeny na stejném počítači: AMD Phenom II X6 1090 T 3,20 GHz, 8 GB RAM, 64 bitový operační systém).

MODELOVÁNÍ KONSTRUKCÍ
Modelování strojů a jejich základu
K modelování strojního zařízení lze zaujmout dva přístupy. První z nich je vytvoření výpočtového modelu konstrukce bez modelu soustrojí, účinky stroje jsou zohledněny jako budící síly (to jsou síly od stroje v místě kotvení a jeho uložení). Výhodou je zjednodušení výpočtového modelu konstrukce. Nevýhodou je nutnost přesného převedení účinků stroje na soustavu budících sil, jejichž určení není snadné.

Většina strojů je uložena na základové konstrukci, která přenáší statické a dynamické zatížení vyvozené strojem do podzákladí. Z konstrukčního hlediska se základy dělí na masivní a rámové. Masivní základy se chovají jako tuhé těleso. Rámové se skládají ze svislých (sloupy) a vodorovných (příčle, desky) nosných prvků, a umožňují tak využití prostoru pod strojem.

Obecně lze ale říci, že vytváření výpočtového modelu stroje se základem není příliš komplikované.

MODELOVÁNÍ PODZÁKLADÍ
Boussinesqův model
pružného poloprostoru je modelován jako homogenní izotropní podloží, které je charakterizováno dvěma materiálovými konstantami E a v. Je popsán jako plně trojrozměrný u (x, y, z) ≠ 0, v (x, y, z) ≠ 0, w (x, y, z) ≠ 0. Podrobný popis lze nalézt v [4].

Westergaardův model
pružného poloprostoru je modelován jako homogenní anizotropní podloží, charakterizován konstantami E a v. Jsou zavedeny kinematické předpoklady u (x, y, z) = 0, v (x, y, z) = 0, w (x, y, z) ≠ 0.

Winklerův (Fuss-Zimmermannův) model podzákladí
Je jednoparametrický dvojdimenzionální model podzákladí zanedbávající smykové napětí. Předpokládá nulové vodorovné deformace. Vychází z předpokladu redukce dimenze w (x, y, z) = w (x, y) · ψ (z), kde funkce musí splnit podmínky ψ (0) = 1, ψ (h) = 0. Pod každým bodem základové konstrukce je napětí přímo úměrné svislému průhybu. Z toho plyne nevýhoda tohoto modelu – a to nespojitost deformací (v bezprostředním okolí základu je nulová deformace). Dalším problémem je určení konstanty C, která není konstantní (je funkcí velikosti a tvaru zatěžovací plochy, nelze užít přímo z výsledků polních zkoušek) [2].

Pasternakův model podzákladí
Je roršířený Winklerův model podzákladí o vliv smykových sil. Vychází také z předpokladu redukce dimenze w (x, y, z) = w (x, y) · ψ (z), kde funkce ψ musí splnit podmínky ψ (0) = 1, ψ (h) = 0. Na rozdíl od Winklerova modelu je schopen postihnout poklesovou kotlinu [2].

Efektivní model podzákladí (Kolář, Němec)
Je povrchový model podzákladí založený na redukci dimenze 3D → 2D, dále 2D → 1D. Umožňuje tak velice věrně vystihnout chování podzákladí pouze oblastí základové spáry. Lze tak počítat interakci stavby s podzákladím bez zvýšení počtu stupňů volnosti. Je zavedena celá řada dalších konstant a tento model podzákladí je obsažen v komerčních programech IDA NEXIS, SCIA ESA PT a Dlubal RFEM pod názvem SOILIN. Podrobný popis lze nalézt v [1], [2] a [3].

Prostorový model MKP
Všechny výše uvedené modely přistupovaly k podzákladí pouze z hlediska vyjádření jeho tuhosti. V úlohách dynamiky je však nutné počítat s hmotným podzákladím, protože jeho kmitající hmota značně ovlivní modální charakteristiky řešeného systému konstrukce- podzákladí. Možností jak modelovat hmotné podzákladí je prostorový MKP model podzákladí, který přináší řadu výhod jako snadné zavedení nehomogenity a anizotropie. Model podzákladí má ale i své nevýhody plynoucí z jeho ohraničenosti. Je to především otázka volby velikosti modelované oblasti podzákladí, dělení na konečné prvky a zvolení okrajových podmínek na hranici modelované oblasti podzákladí. Například dle [5] je v rovinné úloze model podzákladí modelován do vzdálenosti 116 m od konstrukce 35 konečnými prvky. Prostorový model také klade značně vyšší nároky na výpočetní techniku.

Prostorový model MKP s okrajovou podmínkou nekonečného prvku
Novinkou je modelování hranice modelu podzákladí pomocí nekonečného prvku v jednom či ve více směrech. V článku Yun C. B. a Kim J. M. [6] jsou použity v rovinné úloze nekonečné prvky typu HIE (horizontal infinite element), VIE (vertical infinite element) a CIE (corner infinite element).

METODA ŘEŠENÍ
Modální analýza
Modální analýza (úloha o vlastních hodnotách, zobecněný problém vlastních hodnot) je základní úlohou dynamiky. Výpočet frekvencí a tvarů vlastního kmitání je nedílnou součástí dynamického posouzení všech konstrukcí (strojů, základů, lávek, mostů, stožárů, komínů, atd.). Modální analýza je také nezbytnou součástí výpočtu dynamické odezvy metodou rozkladu podle vlastních tvarů kmitu.

Některé metody řešení úlohy vlastních hodnot: přímé řešení
charakteristického polynomu (např. pomocí Sturmovy posloupnosti STURM SEQUENCE CHECK), inverzní iterace (INVERSE ITERATION), iterace podprostoru (BLOCK SUBSPACE ITERATION), Lanczosova metoda, blokový Lanczosův algoritmus (LANCZOS and BLOCK LANCZOS ALGORITHM), redukovaná soustava pomoci Guynovy redukce (REDUCED). Podrobný teoretický popis výše popsaných metod lze nalézt v [7] a [10].

POPIS ŘEŠENÉ KONSTRUKCE
Řešenou konstrukcí je železobetonový základ stolového typu.

Popis soustrojí
Soustrojí je tvořeno hnací parní turbínou a hnaným odstředivým kompresorem. Soustrojí je usazeno na horní desce stolového základu, do které je kotveno šrouby.

Popis základové konstrukce
Soustrojí je uloženo na silně vyztužený železobetonový základ stolového typu. Horní deska o rozměrech 9 420 × 5 900 × 1 000 (délka × šířka × tloušťka, v mm) je nesena čtyřmi sloupy čtvercového průřezu 800 × 800 mm, délky 2 510 mm. Dolní základová deska o rozměrech 8 800 × 5 900 × 1 200 (délka × šířka × tloušťka, v mm) je uložena na dvanácti beraněných prefabrikovaných pilotách čtvercového průřezu 400 × 400 mm, délky 11 500 mm.

Popis podzákladí
Z měření rychlosti šíření tlakových a smykových vln v zemině byla získána funkční závislost velikosti dynamického smykového modulu pružnosti na hloubce. Dále byla stanovena hodnota Poissonova součinitele a objemové hmotnosti.

VÝPOČTOVÝ MODEL
Při vytváření modelů bylo využito jazyka APDL [7], [8], [9]. Byl sestaven algoritmus, který generuje model podzákladí požadovaných vlastností (velikost, tvar, diskretizace, okrajová podmínka, materiálové charakteristiky).

Model soustrojí
Soustrojí je nahrazeno deskami, které jsou modelovány za použití prvku SHELL43 s různou hustotou tak, aby hmotnost a těžiště modelu soustrojí odpovídalo výkresové dokumentaci. Pro dorovnání hmoty byly proto přidány tři prvky MASS21 o celkové hmotnosti 311,61 kg. Protože skutečná hmotnost soustrojí je tímto způsobem nahrazena, jsou ostatní části modelovány za použití prvku SOLID45 jako izotropní materiál s nulovou objemovou hmotností.

Model podzákladí
Je vytvořen v 54 variantách a to tak, aby bylo možno sledovat vliv daných vlastností modelu podzákladí na modální charakteristiky. Všechny modely jsou vytvořeny z prvků SOLID45 s měnícími se materiálovými charakteristikami ve vertikálním směru.

U modelu podzákladí jsou měněny následující parametry:

1. Tvar modelu podzákladí – tvar válce, tvar kvádru.
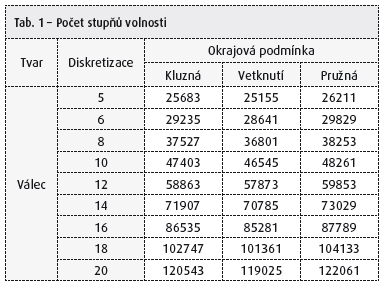
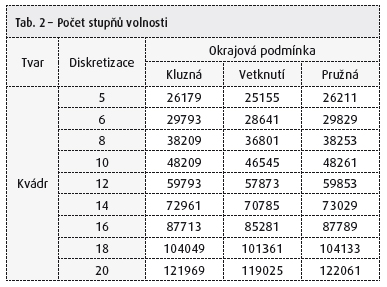
2. Stupeň diskretizace – počet konečných prvků od základové konstrukce po hranici modelované oblasti modelu podzákladí {5, 6, 8, 10, 12, 14, 16, 18, 20}.
3. Okrajová podmínka na svislé hranici modelované oblasti podzákladí – kluzná, poddajná (Winkler), vetknutí.

VÝSLEDKY ANALÝZ
Je počítáno 10 000 tvarů a frekvencí vlastního kmitání metodou blokového Lanczosova algoritmu.

ZÁVĚR
Je nutno zdůraznit, že problematika interakce konstrukce s podzákladím v úlohách dynamiky (modální analýza, harmonická analýza, odezva v časové oblasti) je široká. Existuje mnoho modelů podzákladí, z nichž většina je vhodná pouze pro řešení statické odezvy. Každý model podzákladí přináší určité zjednodušení. Velice vhodným způsobem modelování oblasti podzákladí je 3D varianta metodou konečných prvků. Je zde však také mnoho otázek týkajících se vlastností modelu podzákladí (jeho velikosti, tvaru, stupně diskretizace, okrajové podmínky na hranici).

Z výsledků modální analýzy vyplývá, že způsob modelování oblasti podzákladí výrazně ovlivňuje modální charakteristiky řešené konstrukce, dochází ke zhuštění spektra a ke změně hodnot frekvencí vlastního kmitání. Je tedy nutné řešit odezvu konstrukce na dynamické zatížení v interakci s podzákladím, problematiku interakce dále studovat, provádět numerické simulace a měření pro verifikaci výsledků.

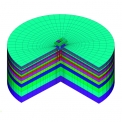
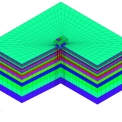
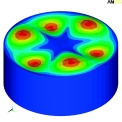
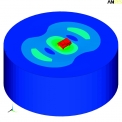
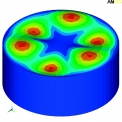
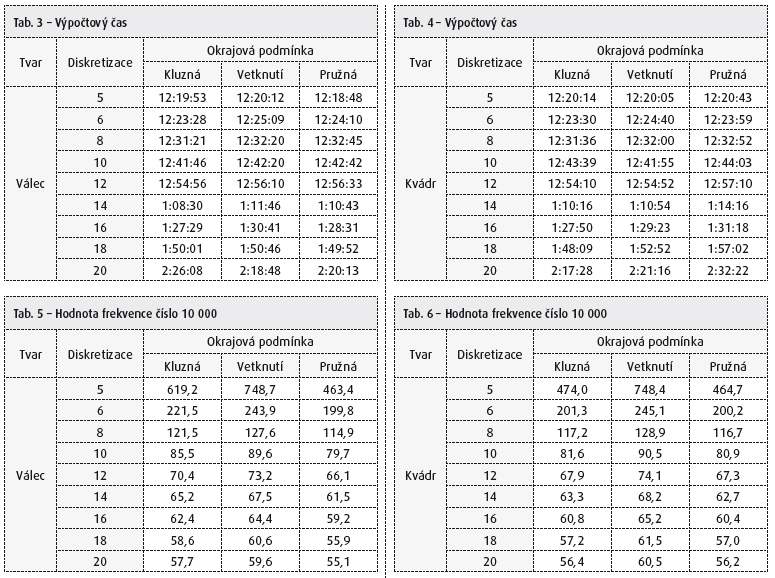
Z tab. 3, tab. 4, tab. 5 a tab. 6 je patrné, že sledované dvě varianty tvaru modelu podzákladí (kvádr a válec) nemají vliv na výpočtový čas a na hodnoty vlastních frekvencí. Bylo zjištěno, že některé tvary vlastního kmitání u modelu podzákladí ve tvaru válce jsou pro řešení dynamické odezvy konstrukce nevýznamné. Tvary vlastního kmitání samotného podzákladí a tvary konstrukce s podzákladím jsou jasně rozlišitelné (viz obr. 2, obr. 3). Vlastní tvary kmitání zeminového bloku neovlivněné konstrukcí lze získat výpočtem modální analýzy modelu podzákladí bez konstrukce (viz obr. 4).

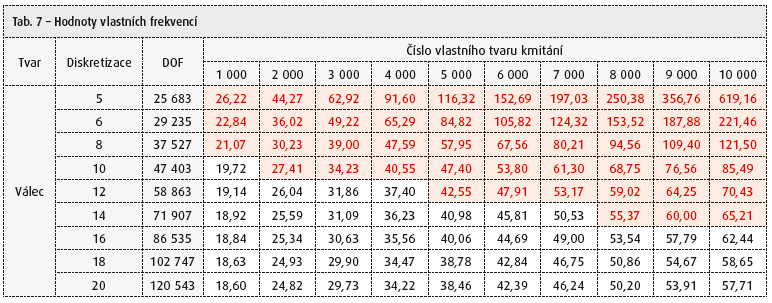
Velice významným parametrem je stupeň diskretizace, tedy dělení modelu na konečné prvky. Tento parametr má vliv na výsledný počet stupňů volnosti a tím také ovlivňuje výpočtový čas a objem výsledných dat. Dělení modelu na konečné prvky nám také určuje, jakou maximální frekvenci vlastního kmitání je model podzákladí schopen správně vystihnout. Všechny vyšší frekvence jsou odfiltrovány. Na tuto skutečnost musíme brát ohled při řešení dalších úloh dynamiky např. při harmonické analýze, analýze v časové oblasti (transientní analýze) a při řešení seismické odezvy metodou lineárních spekter odezvy. Z tab. 7 je patrná nutnost zvolení vhodné diskretizace modelované oblasti podzákladí s ohledem na požadovanou hodnotu maximální počítané frekvence vlastního kmitání.

Hodnoty vlastních frekvencí jsou do značné míry ovlivněny typem okrajové podmínky na hranici modelované oblasti podzákladí. Porovnáme-li vliv typu okrajové podmínky s vlivem diskretizace, lze konstatovat, že vliv typu okrajové podmínky je zanedbatelný.

Vliv okrajové podmínky je nepřímo úměrný velikosti modelované oblasti podzákladí. Tento vliv je znatelně menší u modelu podzákladí ve tvaru válce. Vliv velikosti modelované oblasti podzákladí podrobněji řeší práce [11].

Prezentované výsledky byly získány za podpory specifického výzkumu FAST-J-10-29.

Literatura :
[1] Němec I. Modelování interakce stavby s podložím
[2] Kolář V., Němec I. Modelling of soil-structure interaction, Academia, Praha, 1990
[3] Kolář V., Němec I. Contact Stress and Settlement in the Structure-Soil, Academia, Praha, 1991
[4] Boussinesq J. Application des potentiels a l’etude de l equilibre et du mouvement des solides elastiques, Gauthier-Villars, Paris, 1885
[5] Kellezi L. Local Transmitting Bounderies for Transient Elastic Analysis, Soil Dynamics and Earthquake Engineering, Elsevier, 2000
[6] Yun C. B., Kim J. M. Dynamic Infinite Elements for Soil-Structure Interaction Analysis in a Layered Soil Medium, Computational Methods in Engineering and Science EPMESC X, Sanya, Hainan, China, 2006
[7] ANSYS, Inc. Theory, Repase 11, 2007
[8] ANSYS Modeling and Meshing Guide, ANSYS Release 9.0, 2004
[9] ANSYS Structure Analysis Guide, ANSYS Release 9.0, 2004
[10] Wilson E. L. Three-Dimensional Static and Dynamic Analysis of Structures, Computers and Structures Inc., Berkeley California USA, Third Edition 2002
[11] Martinásek J. Dynamická analýza základové konstrukce pod kompresor: Brno, 2008

Numerical Analysis of Parameters of MKP Subsoil model on The modal Characteristics of The Subsoil-Construction System
The work deals with issues of soil-structure interaction (SSI). Solved structure is a reinforced concrete table-top foundation under the compressor with turbine. Dynamic response of the structure is strongly influenced by subsoil. It is therefore necessary to create a computational model of the structure including the subsoil. The spatial model of subsoil places considerable demands on computing time and data volume. The computational model of the structure including the subsoil is composed of FEM program system ANSYS. It is a study of the influence of shape, discretization and boundary conditions on the modal characteristics of the construction-foundation-subsoil system.

Autor

• Ing. Martinásek Josef