Numerická analýza vlivu parametrů a typu okrajové podmínky na velikost amplitudy odražené vlny v zemním prostředí řešená metodou konečných prvků

NETLUMENÉ VLNĚNÍ ŠÍŘÍCÍ SE PROSTOREM A POLOPROSTOREM
Odvozením pohybové rovnice prostorového vlnění šířícího se prostorem a jejím řešením se zabývala řada autorů, jako Timoshenko s Goodierem [1], Kolsky [2], Ewing s Jardetzkym a Pressem [3], Grant s Westem [4] a další. Odvození pohybové rovnice lze provést sestavením dynamických silových podmínek rovnováhy pomocí 2. Newtonova zákona nebo d´Alembertova principu. Výsledná soustava pohybových rovnic má pak následující tvar:

Řešení těchto pohybových rovnic lze nalézt ve dvou variantách pro vlnění šířící se prostorem. První (primární vlnění, P-vlna) představuje vlnění čisté objemové změny (bez rotace) a získáme jej derivováním jednotlivých výrazů (1), prvního podle X, druhého podle Y, třetího podle Z, a jejich následným sečtením. Druhé řešení (sekundární vlnění, S-vlna) představuje vlnění čisté rotace (bez objemové změny) a získáme jej derivováním výrazů (1), druhého podle Z a třetího podle Y, a jejich následným rozdílem eliminujeme f. Nyní definujme rychlost částic média jako u $ a vyjádřeme vztah rychlostí šíření vlnění a rychlosti pohybu částic média.

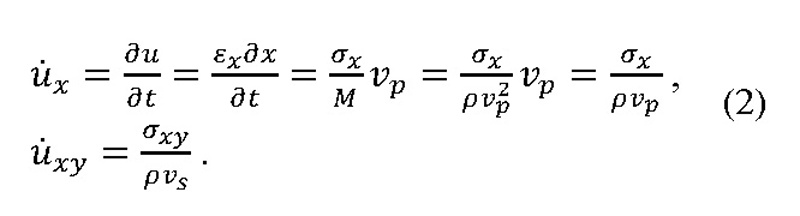
Rychlost vlnění a rychlost částic jsou ve stejném (opačném) směru, je-li aplikováno tlakové (tahové) napětí. Rychlost částic je na rozdíl od rychlosti vlnění funkce intenzity napětí.

Za předpokladu elastického homogenního poloprostoru můžeme nalézt další dvě řešení pohybových rovnic (1). Prvním řešením je Rayleigho vlna (R-vlna), jejímž studiem se zabýval Lord Rayleigh [7] a dále ji detailně popsal Lamb [5]. Jedná se o rovinnou vlnu šířící se ve směru osy X jejíž pohyb částic není závislý na souřadnici (s povrchem definovaným rovinnou XY). K pohybu částic dochází pouze ve směru os X a Z, tedy u ≠ 0, v = 0, w ≠ 0. Druhým řešením je Loveova vlna (L-vlna), jejímž studiem se zabýval A. E. H. Love, jedná se o rovinnou vlnu šířící se ve směru osy X jejíž pohyb částic není závislý na souřadnici y (tedy δ/δy = 0) (s povrchem definovaným rovinnou XY). K pohybu částic dochází pouze ve směru osy Y, tedy u = 0, v ≠ 0, w = 0.

RAYLEIGHO VLNA ŠÍŘÍCÍ SE POLOPROSTOREM S ROZHRANÍM MATERIÁLŮ
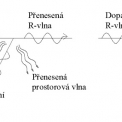
Problém dopadající R‑vlny na společné rozhraní dvou čtvrtprostorů není v současné době stále vyřešen. Můžeme však konstatovat že vzniká odražená R-vlna, odražená prostorová vlna, přenesená R‑vlna, přenesená prostorová vlna a vlna na rozhraní čtvrtprostorů (viz obr. 1a). Rozdělení energie mezi jednotlivé vlny je funkcí úhlu rozhraní a materiálových charakteristik obou prostředí.

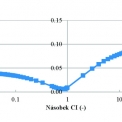
Podrobněji je prostudována problematika dopadu a následného odrazu a lomu R-vlny do rohu čtvrtprostoru (viz obr. 1b, zvláštní případ varianty a, kdy druhý čtvrtprostor má nulové parametry). Touto problematikou se zabývala řada autorů, jako Viktorov [8], deBremaecker [9], Knopoff s Gangim [10], Pilant a kol. [11], Kane se Spencem [12] a další. Množství energie nesené jednotlivými odraženými vlnami je funkce součinitele příčné kontrakce a rohového úhlu. Poměr energie odražené vlny k energii vlny dopadající vyjádřili autoři Viktorov, deBremaecker, Pilant a kol. Jejich výsledky posléze porovnal a shrnul Richart s Hallem a Woodsem v následujícím grafu.

POPIS VÝPOČTOVÉHO MODELU
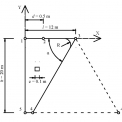
Výpočtový model je tvořen poddajnou deskou umístěnou na horním povrchu bloku zeminy. Kruhová deska o poloměru 1 m je modelována jako zcela poddajná (s nulovou tuhostí). Zemina je modelována jako homogenní izotropní materiál (modul pružnosti E = 50 MPa, součinitel příčné kontrakce v = 0,3, hustota ρ = 2 000 kg/m³). Model podzákladí o výšce 20 m a poloměru 12 m je modelován plošnými prvky PLANE182 (rotační symetrie). Hranice modelu podzákladí je modelována v různých variantách sklonu α = (60, 120)°. Okrajová podmínka na svislé hranice je modelována jako: (i) kluzná, (ii) vetknutí, (iii) Winklerova pružná okrajová podmínka (SURF153, kolmá na hranici, v rovnoběžném směru s hranicí je tuhost nulová) se součinitelem ložnosti podzákladí C = (5E4, 5E9) kN/m³, (iv) disipativní okrajová podmínka (KOMBIN14, kolmá na hranici) s koeficientem viskózního tlumení c = (1E4, 1E7) Ns/m, (v) bez okrajové podmínky (volná hranice), (vi) vazkopružná okrajová podmínka (kombinace pružné a disipativní okrajové podmínky) modelovaná kolmo i rovnoběžně s hranicí (viz dále). Okrajová podmínka na spodní vodorovné hranici je modelována jako vetknutí. Schéma řešené úlohy je zobrazeno na obr. 3. Zatížení působící na horním povrchu desky ve směru záporné osy Y je znázorněno na obr. 4.

Ad (vi) vazkopružná okrajová podmínka (KOMBIN14) je modelována v několika variantách násobcích „ideální“ tuhosti a koeficientu viskózního tlumení, jejichž výpočet je popsán v následujícím textu. Tuhost kolmá na hranici je získána ze vztahu pro výpočet tuhosti pružiny kolmo na zatěžovanou kruhovou plochu (v našem případě 1 m²) uvedeného v Timoshenko, Goodier [1]:

Hodnota koeficientu viskózního tlumení kolmého na hranici je získána dosazením vztahu rychlosti kmitání částic média a napětí (2) do následujícího výrazu pro výpočet reakce: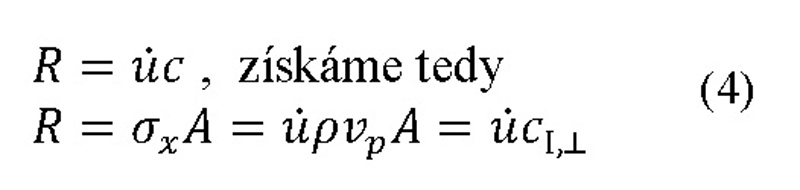

kde:
Koeficient viskózního tlumení „ideálního“ tlumiče kolmo na hranici modelu.

Koeficient viskózního tlumení rovnoběžný s hranicí obdržíme stejným způsobem ve tvaru:

Tuhost rovnoběžná s hranicí je pak vyjádřena jako:

Protože úloha je řešena jako osově symetrický 2D problém, musíme výše uvedené výrazy pro tuhosti a koeficienty tlumení přenásobit hodnotou , protože reakce jsou počítány na povrch celého válce. Získáme tak následující hodnoty: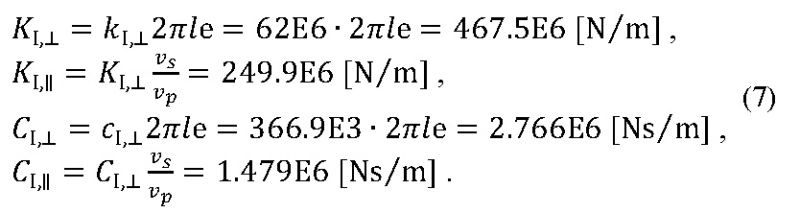


Odezva na dané zatížení je řešena v časové oblasti implicitní Newmarkovou metodou do konečného času 0,5 s, s časovým krokem 5E^-4 s. Tlumení je modelováno Rayleigho útlumem s parametry α = 8,0784, β = 1,5158.10^-4 .

Pro snazší orientaci a přehlednost je zavedeno následné zkrácené značení modelů:

ZN1, ZN2, ZN3, ZN4 (8)

kde:

ZN1 číslo sledovaného uzlu

viz obr. 3,

ZN2 sledovaná veličina

UY = výchylka ve směru Y,

ZN3 okrajová podmínka

K = kluzná,
V = vetknutí,
Wnum = pružní Winklerova (num = tuhost),
Cnum = disipativní o.p. (num = parametr viskózního tlumení),
B = bez okrajové podmínky,
numCI = násobek „ideálního“ koef. vis. tlum.,
numKI = násobek „ideální“ tuhosti,

ZN4 poloměr zaoblení

Rnum = poloměr zaoblení s příslušnou hodnotou,
Není-li uveden, je poloměr nulový.

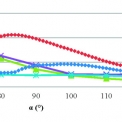
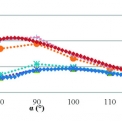
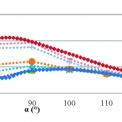
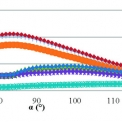
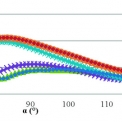
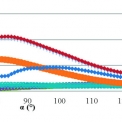
Odezva modelu poddajné desky na dané buzení v časové oblasti je zobrazena na grafech.

ZÁVĚR
Z uvedených výsledků lze konstatovat následující závěry:

• Na rozdíl od jednodimenzionální úlohy, kde odražená vlny má stejnou velikost amplitudy (opačného znaménka) při odrazu od nekonečně tuhé hranice (vetknutí) a volné hranice (bez okrajové podmínky), je v prostorové úloze (s šířící se povrchovou vlnou) amplituda odražené vlny u nekonečně tuhé a volné hranice různá a závisí na úhlu α (rohový úhel). Amplituda odražené vlny od volné hranice je ve srovnání s amplitudou odražené od nekonečně tuhé hranice (vetknutí) značně menší. Amplituda odražené vlny s volnou hranicí má své minimum pro α ϵ {78,84}°, což se shoduje s teoretickými závěry, které udávají lokální minimum energie odražené R-vlny pro úhly a blízké 80 ° (obr. 2). Lokální minimum amplitudy odražené vlny od nekonečně tuhé hranice je pro úhel α = 73°.
• U modelů se „zaoblením“ rohu je amplituda odražené vlny od nekonečně tuhé hranice se zaoblením menší než amplituda odražené vlny od volné hranice se zaoblením (dokonce je v celém intervalu menší než amplituda odražené vlny od volné hranice bez zaoblení).
• Amplituda odražené vlny modelů s pružnou Winklerovou okrajovou podmínkou se nachází téměř pro všechny případy mezi amplitudou pro nekonečně tuhou hranicí a amplitudou pro volnou hranici. Obecně lze říci, že s rostoucí hodnotou tuhosti (koeficientu ložnosti) se odezva blíží odezvě s nekonečně tuhou hranicí. Pro úhel α = 70° se amplituda odražené vlny s pružnou okrajovou podmínkou (nezávisle na tuhosti) blíží amplitudě odražené vlny s volnou hranicí.
• Naprosto stejné závěry (předcházející bod) platí pro disipativní okrajovou podmínku.
• Amplituda odezvy modelu s okrajovou podmínkou násobku „ideálního“ koeficientu viskózního tlumení se pro násobitel 1 blíží nule (má minimum pro α ϵ {79,82}° a je značně menší než amplituda odražené vlny od volné hranice). Amplituda odražené vlny se jednostranně blíží k amplitudě odražené vlny od volné hranice, je-li násobitel menší než 1 a jde-li k nule. Amplituda odražené vlny se jednostranně blíží k amplitudě odražené vlny od nekonečně tuhé hranice, je-li násobitel větší než 1 a jde-li k nekonečnu.
• Amplituda odezvy modelu s okrajovou podmínkou násobku „ideální“ tuhosti se pro násobitel 1 nachází mezi amplitudou s nekonečně tuhou hranicí a amplitudou s volnou hranicí. Amplituda odražené vlny se nejednostranně (v závislosti na α) blíží k amplitudě odražené vlny od volné hranice, je-li násobitel menší než 1 a jde-li k nule. Amplituda odražené vlny se nejednostranně (v závislosti na α) blíží k amplitudě odražené vlny od nekonečně tuhé hranice, je-li násobitel větší než 1 a jde-li k nekonečnu.
• Amplituda odražené vlny u modelů s vazkopružnou okrajovou podmínkou (kombinace „ideální“ tuhosti a „ideálního“ koeficientu viskózního tlumení) je minimální pro kombinace s násobkem ideálního koeficientu tlumení 1 a násobkem ideální tuhosti 0 nebo 0,01 (tyto odezvy jsou si vzájemně velmi blízké). Pro kombinaci 1CI nastane minimum odražené amplitudy pro α = 82°, pro kombinaci 1CI_0.01KI nastane minimum odražené amplitudy pro α = 80°, což je globální minimum ze všech řešených variant.
• Dále byl proveden výpočet pro rohový úhel α = 90° pro řadu hodnot násobitele „ideální“ hodnoty viskózního tlumení (bez „ideální“ tuhosti). Je zřejmé, že minimální hodnoty amplitudy odražené vlny jsou dosaženy pouze pro násobitel blízký jedničce (zleva) (viz graf 7). Minimální hodnota amplitudy odražené vlny nastane pro násobitel 0,9.

LITERATURA:
[1] Timoshenko S.P., Goodier J.N. Theory of Elasticity, McGraw – Hill Book Co, New York, 1951.
[2] Kolsky H. Stress Waves in Solids, Dover Publications, Inc. (New York) and Clarendon Press (Oxford), 1953.
[3] Ewing W.M., Jardetzky W.S., Press F. Elastic Waves in Layered Media, McGraw-Hill Book Co., New York, 1957.
[4] Grant F.S., West G.F. Interpretation Theory in Applied Geophysics, McGraw-Hill Book Co., New York, 1965.
[5] Lamb H. On the Propagation of Tremors over the Surface of an Elastic Solid, Philosophical Transactions of the Royal Society, London, 1904.
[6] Richart F.E. Jr., Hall J.R. Jr., Woods R.D. Vibrations of Soils and Foundations, Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1970.
[7] Rayleigh Lord On Waves Propagated Along the Plane Surface of an Elastic Solid, London Mathematical Society Proc., 1885.
[8] Viktorov I.A. The Effects of Surface Defects on the Propagation of Rayleigh Waves, Soviet Physics, Doklady, 1958.
[9] deBremaecker J.Cl. Transmission and Reflection of Rayleigh Waves at Corners, Geophysics, Vol. 23, 1958.
[10] Knopoff L., Gangi A.F. Transmission and Reflection of Rayleigh Waves by Weges, Geophysics, Vol. 25, 1960.
[11] Pilant W.L., Knopoff L., Schwab F. Transmission and Relflection of Surface Waves at a Corner, 3, Rayleigh Waves (Experimental), J. Geophysical Research, Vol. 69, No. 2, 1964.
[12] Kane J., Spence J. Reyleigh Transmission on Elastic Wedges, Geophysics, Vol. 28, No. 5, 1963.

Numerical analysis of the influence of parameters and the type of boundary conditions on the amplitude of the reflected wave in the soil medium solved by finite element method
The results of dynamics of analyses dedicated to the issue of soil-structure interaction are influenced with reflected wave from the boundary of the modeled area of FEM model. This paper deals with the quantification of the impact of different boundary conditions with changing slope of the model boundary.

Autor

• Ing. Martinásek Josef