Některé možnosti modelování betonových konstrukcí při nelineární analýze

• Foto

KONSTITUTIVNÍ MODELY BETONU
Problematice modelování chování betonu je věnována velká pozornost ve výzkumu a odborných betonářských společnostech. Vznikla celá řada doporučení a modelů betonu, které mají různou míru výstižnosti chování betonu, požadavky na vstupní informace a výpočetní náročnost. V článku diskutované základní konstitutivní modely pro rovinné úlohy mohou být rozděleny do těchto skupin:

• zjednodušené konstitutivní modely betonu s predikcí zón namáhání (Materiálový model 1 – Podmínka plasticity von Mises a lineární zpevnění),
• pružnoplastické konstitutivní modely betonu (Materiálový model 2 – Chenova podmínka plasticity a model zpevnění vypracovaný Ohtanim),
• konstitutivní modely betonu založené na lomové mechanice (Materiálový model 3 – Kupferova podmínka porušení a lomová mechanika).

Zjednodušené konstitutivní modely betonu s predikcí zón namáhání se mohou použít v případech, kdy je pro nelineární analýzu nedostatek vstupních informací o vlastnostech betonu nebo dostupný výpočetní systém nepodporuje konstitutivní modely betonu. Pro tento typ konstitutivních modelů lze použít podmínku plasticity von Mises a lineární zpevnění. Při výpočtu s tímto konstitutivním modelem je nutné provést rozdělení výpočetního modelu konstrukce na oblasti dle namáhání a v nich uplatnit odpovídající hodnoty materiálových pevností a plasticity. Při predikci zón namáhání se musí také zohlednit možný rozvoj plastických oblastí.

Pružnoplastické konstitutivní modely betonu se snaží respektovat různé chování betonu v tlaku a tahu. Zvolený konstitutivní model kombinuje Chenovu podmínku plasticity [1] a model zpevnění vypracovaný Ohtanim [2]. Model vznikl na základě experimentů. Konstitutivní modely betonu založené na lomové mechanice patří v současné době k nejrozšířenějším, mezi nejznámější patří model SBETA [3] ve výpočetním systému ATENA. Porušení betonu se vyhodnocuje Kupferovou podmínkou porušení [4], která je podobná Chenově podmínce plasticity. Konstitutivní modely betonu založené na lomové mechanice používají další materiálový parametr – lomová energie. Nejznámější model SBETA vznikl v souladu s doporučeními v [5]. Princip modelu spočívá v tom, že po detekci vzniku trhlin je upravován vztah mezi napětím a poměrným přetvořením v závislosti na míře otevření trhliny. Problematikou konstitutivních modelů betonů a fyzikálně nelineární analýzy se podrobně zabývá [6].

NELINEÁRNÍ ANALÝZA
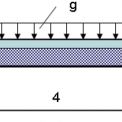
Uvedené konstitutivní modely betonu byly ověřovány na rovinném výpočetním modelu nosníku o rozpětí 6 m a šířce 0,2 m a třech různých výškách. Uváděné výsledky jsou platné pro nosník vysoký 0,75 m. Konstrukce je zatížená spojitým zatížením g = 20 kN/m po celé délce. Nosník je uložen na krajích na svislých neposuvných podporách a na levém okraji je horizontální neposuvná podpora. Pro rovinné výpočetní modely byl zvolen izoparametrický konečný prvek se čtyřmi uzly [7]. Uvedený konečný prvek byl použit ve výpočtech v systému ANSYS [8] a uFEM [9].

MATERIÁLOVÉ MODELY PRO NELINEÁRNÍ VÝPOČET
Pro uvedené konstitutivní modely betonu jsou vytvořeny tři materiálové modely. Společnými parametry materiálových modelů jsou:

• modul pružnosti E_c = 30,0 GPa,
• součinitel příčné kontrakce ν = 0,2,
• pevnost v tahu F_tah = 2,2 MPa,
• pevnost v tlaku F_tlak = 25,0 MPa.

Zbylé parametry jsou specifické pro každý materiálový model. Výchozím materiálem je beton C20/25. Zbylé specifické hodnoty vlastností materiálových modelů jsou převzaty z obdobných modelů používaných v doporučeních CEB-FIB.

NELINEÁRNÍ VÝPOČET
Výpočty se prováděly ve dvou výpočetních systémech. Chenova podmínka plasticity v kombinaci s Ohtaniho modelem zpevnění a model rozmazaných trhlin byly používány ve výpočetním systému uFEM [9]. Ve výpočetním systému ANSYS [8] se zkoumala podmínka plasticity von Mises s lineárním modelem zpevnění. Konečně-prvkové modely byly v obou systémech stejné. V lineárním výpočtu byly výsledky deformací získané v obou uvedených programech téměř stejné a odchylka vertikálního posunutí uy je pouze 0,00002 m.

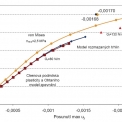
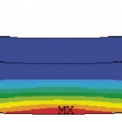
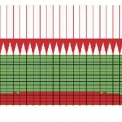
Pro aplikaci podmínky von Mises je nutné vytvořit na výpočetním modelu dvě oblasti s různými materiálovými vlastnostmi. Tento postup je nutný, protože u podmínky von Mises se předpokládá, že materiál má stejnou pevnost v tlaku a tahu. Tlakové a tahové vlastnosti betonu jsou ovšem velmi výrazně odlišné. Možnost plastizace se v modelu připouští pouze ve vyšrafované oblasti (oblast namáhaná tahem) na obr. 1. Ve zbylé části se předpokládá lineární chování materiálu, protože zde nejsou dosahovány vysoké hodnoty tahových napětí. Na obr. 2 jsou srovnány výsledky dosažené pomocí jednotlivých konstitutivních modelů.

ZHODNOCENÍ VÝSLEDKŮ NELINEÁRNÍHO VÝPOČTU
Při provedených nelineárních výpočtech byl sledován vliv použitého konstitutivního modelu na dosahované výsledky. Z hlediska výstižnosti se ve všech sledovaných úlohách jako nejvhodnější jeví používání materiálového modelu založeného na principech nelineární lomové mechaniky (modelu rozmazaných trhlin). Pružnoplastický model využívající Chen-Chenovu podmínku porušení a Ohtaniho model zpevnění umožňuje, ve studovaném rozsahu namáhání, získat výsledky velmi blízké výsledkům stanoveným pomocí modelu rozmazaných trhlin. Protože také výpočetní náročnost je při použití pružnoplastického modelu výrazně nižší než u modelu rozmazaných trhlin, je v řadě úloh jeho použití velmi vhodné.

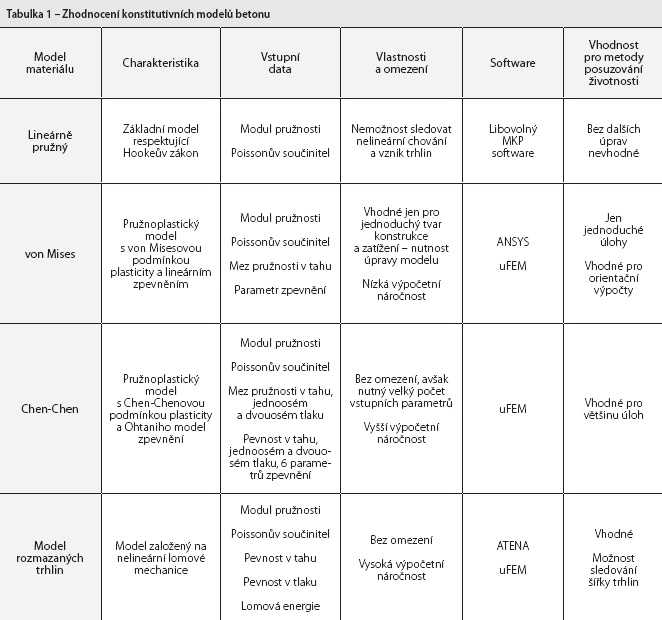
Předností modelu rozmazaných trhlin naopak může být možnost sledování celkové šířky trhlin, pokud je potřeba tento parametr zahrnout do posudků. Nevýhodou Chen-Chenova modelu je potřeba znalosti vyššího počtu vstupních parametrů, které nemusí být dostupné (zejména parametry funkce zpevnění je třeba stanovovat na základě laboratorních zkoušek materiálu). Ve vybraných úlohách (orientační a předběžné analýzy apod.) je možné úspěšně použít i zjednodušený model využívající von Misesovu podmínku plasticity. V tomto případě je nutno upravit model tak, aby se podmínka uplatnila jen u tažených částí konstrukce. To omezuje jeho využití jen na úlohy s jednoduchým tvarem a zatížením. Zhodnocení konstitutivních modelů betonu uvádí tabulka 1.

Tento výsledek byl získán za finančního přispění MŠMT ČR, projekt 1M0579, v rámci činnosti výzkumného centra CIDEAS. (This outcome has been achieved with the fi nancial support of the Ministry of Education, Youth and Sports of the Czech Republic, project No. 1M0579, within activities of the CIDEAS research centre.)

LITERATURA:
[1] Chen, A. C. T., Chen, W. F.: Constitutive Relations for Concrete, Journal of the Engineering Mechanics Division ASCE, 1975
[2] O htani, Y., Chen, W. F.: Multiple Hardening Plasticity for Concrete Materials, Journal of the EDM ASCE, 1988
[3] A TENA Program Documentation, CERVENKA CONSULTING, Praha, 2007
[4] K upfer H., Hilsdorf H.,K., Rüsch H.: Behaviour of Concrete Under Biaxial Stress, Journal ACI, Proc. V.66, č. 8, 1969
[5] B azant, Z. P., Planas J. Fracture and Size Effect in Concrete and Other Quasibrittle Materiále. Boca Raton :CRC Press. 1998
[6] B rožovský, J.: Modelování fyzikálně nelineárního chování železobetonových konstrukcí, Ostrava: VŠB-TU Ostrava - FAST, 2003
[7] K OLÁŘ, V. Metoda konečných prvků, Skriptum, Praha: SNTL. 1971.
[8] R ELEASE 11 DOCUMENTATION FOR ANSYS, SAS IP, INC., 2007
[9] u FEM software home page: HTTP://FAST10.VSB.CZ/BROZOVSKY/ARTICLES/UFEM

Some options of modelling concrete structures during non-linear analysis
The shown article evaluates the available possibilities (material and computing models, software) of the non – linear analysis of the elements in the concrete and reinforced concrete structures with the different level of problem‘s simplification with respect to the practical application (the requirements for the input data, the solution severity, the results cogency) and mainly with respect to the application for the tasks of the design, the reliability evaluation and the structures durability.

Autor

• Ing. Sucharda Oldřich