Napjatost v kotevních oblastech předpínací výztuže

Problém lokálních napjatostí je letitý a počátky jeho řešení lze najít např. v [1]. Význam řešení lokálních napjatostí vzrůstá vzhledem k provádění stále subtilnějších konstrukcí. Počet a význam oblastí s lokální napjatostí podstatně vzrostl zavedením předpjatého betonu a v poslední době zejména tím, že se zavádějí do praktického používání stále větší předpínací jednotky.
V tomto článku je řešena napjatost v místě kotvení předpínací výztuže a je provedeno srovnání několika metod výpočtu napětí a výsledných sil v těchto oblastech.

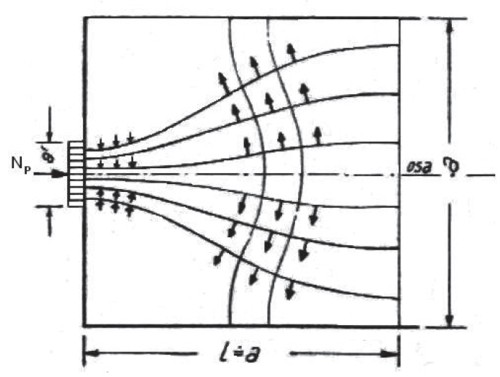
Obr. 1 – Zjednodušené znázornění průběhu siločar pod kotvou [6]

ŘEŠENÍ LOKÁLNÍ NAPJATOSTI POD KOTVOU, OBECNÉ PŘEDPOKLADY ŘEŠENÍ
Podle [5] se napjatost kotevní oblasti vyvozená předpínacími silami a v místech konců nosníků v kombinaci s reakcemi ložisek nedá uspokojivě určit metodou technické pružnosti. Řešení je pracné a vzhledem k plasticitě betonu problematické. Obvykle se pouze stanoví velikost a poloha výslednice příčných tahů v kotevní oblasti, která se zachycuje výztuží.
Při výpočtu napětí v kotevní oblasti je v první řadě nutné určit vlastní velikost této oblasti. Nejčastěji se určuje velikost oblasti pomocí tzv. vyrovnávací délky, tj. délky, na které podle předpokladů dojde k roznesení napětí vzniklého kotvením výztuže na celý příčný řez a průběh napětí po výšce průřezu bude mít lineární charakter.

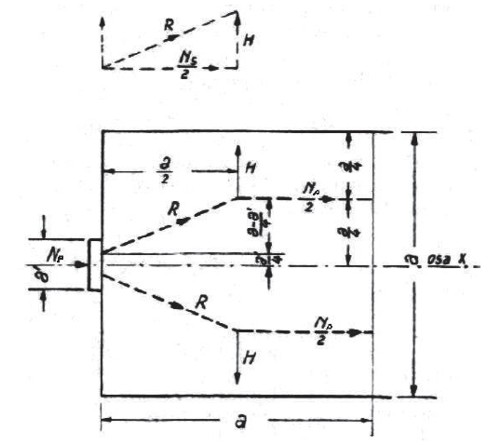
Obr. 2 – Náhradní obrazec sil v betonu pod kotvou [6]

Tuto délku můžeme určit z přesnějšího výpočetního modelu dané oblasti (viz kap. 3) nebo se považuje za vyrovnávací délku největší z následujících rozměrů:

• součet vzdáleností jediné vložky nebo vrstvy vložek v průřezu od protilehlých okrajů průřezu,
• součet vzdáleností protilehlých okrajů průřezu od vložek jim nejbližších,
• vzdálenost dvou sousedních vložek,
• vzdálenost dvou sousedících vložek, měřená v osách geometrických částí průřezu,
• vzdálenost okraje průřezu a vložky tomuto okraji nejbližší, měřená v osách geometrických částí průřezu.

Pro námi zjišťované napětí pod kotvami (nejde o kotvení soudržností) se délka vyrovnávací oblasti rovná délce kotevní oblasti.

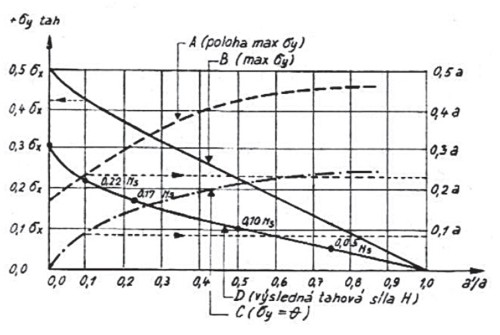
Obr. 3 – Stanovení napětí a sil pod jednoduchou kotevní deskou [3, 6]

Vnitřní síly pod roznášecí deskou řešené příhradovou analogií
Působení síly vyvozené jedním kabelem umístěným centricky v prvku, si podle stávajících výpočtů můžeme představit podle obr. 1 a 2. Pod kotevní deskou se soustředěný tlak rozptýlí v kotevní oblasti na rovnoměrné napětí. Tlakové čáry pak v blízkosti desky mají konvexní tvar a v určité vzdálenosti přecházejí do konkávního tvaru [5]. Na konci kotevní oblasti pak jsou rovnoběžné s vnášenou silou. V konvexní části tlakových čar vzniknou příčné tlaky, v konkávní pak příčné tahy.
Pro přibližné stanovení výsledné příčné tahové síly se dá použít zjednodušeného příhradového modelu (obr. 2). Za předpokladu, že výsledná příčná síla H bude působit v polovině kotevní oblasti a, můžeme z podobnosti trojúhelníků psát:

Tento tah H se musí plně zachytit výztuží.

Podrobnějším zkoumáním kotevních oblastí se zabýval Guyon [3], který sestavil grafy na rozložení těchto tahových napětí od kotevní síly (obr. 3).
 

Rozdělení tohoto napětí závisí na poměru:

Podle vztahu:

 
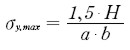
Celý článek včetně všech grafů a vzorců naleznete v ČB. příloze časopisu Konstrukce 2/2008. Možnost předplatného ZDE.

Autoři

• Ing. Šindler Daniel
• Doc. Ing. Hrdoušek Vladislav