Možnosti využití optimalizačních modulů v systému ANSYS

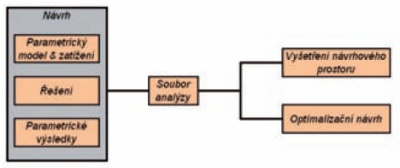
Obr. 1 – Postup řešení optimalizačního problému

Nejedná se však o optimum z matematického hlediska, kterým se podrobně zabývá oblast Matematických operačních systémů. Jde spíše o vytvoření nejefektivnějšího využití konstrukčních požadavků (návrhové a stavové proměnné) za účelem minimalizování, resp. maximalizování určitého cíle (účelové funkce). To je způsobené především výrobními procesy ve stavebnictví, kde jsme omezeni standardizovanými rozměry používaných prvků, či normovými požadavky kladenými na konstrukce. V dnešní době existuje řada softwarů, které mají implementovány ve svých strukturách optimalizační algoritmy, umožňující konstruktérovi vytvořit systém, který lze v oblasti stavebnictví považovat za optimální. Lze zde jmenovat: Optislang, Tosca, OptiStruct a ANSYS.

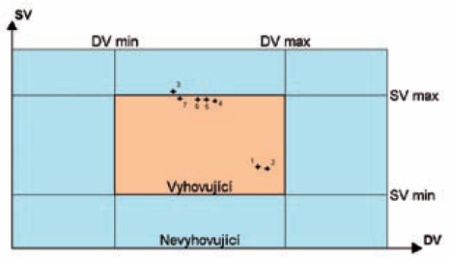
Obr. 2 – Návrhový prostor

ANSYS MODULY OPTIMALIZACE
Poslední ze jmenovaných, ANSYS, je rozsáhlý systém, založený na metodě konečných prvků (MKP), jehož schopností využívá řada modulů pro konkrétní analýzy. Dva z nich jsou využívány pro stanovení efektivního návrhu konstrukce a tj. Design Optimization (Konstrukční optimalizace) a Topological Optimization (Topologická optimalizace). S jejich pomocí lze řešit širokou škálu optimalizačních problémů.

Obr. 3 – Konzolový nosník zatížený osovou silou

KONSTRUKČNÍ (NÁVRHOVÁ) OPTIMALIZACE
(DESIGN OPTIMIZATION)
Je samostatný modul pro řešení optimalizačních problémů, jež je zakomponován v systému Ansys. Jeho pomocí je možné řešit optimalizační problémy na konstrukcích tvořenými konečnými prvky. Avšak lze tohoto modulu využít i při stanovení optimálního řešení bez použití konečných prvků. Umožňuje na základě dvou hlavních metod (metoda iterace podprostoru a gradientní metoda) stanovit řešení přibližující se k optimu.

POSTUP ŘEŠENÍ
Před vlastním řešením, je nutné určit všechny proměnné (optimalizační parametry) ovlivňující návrh prvku, či konstrukce. Optimalizačními parametry jsou:

• Návrhové proměnné (Design variables – DVs) – hodnoty, které se mění během výpočtu až do vytvoření optimálního návrhu. Stanovují se jejich dolní a horní hranice představující omezující oblast pro návrhové proměnné. Lze stanovit až 60 návrhových proměnných.
• Stavové proměnné (State variables – SVs) – hodnoty, představující omezení našeho návrhu. Mohou být stanoveny buď obě omezující hranice stavové proměnné, nebo jen jedna. Ansys umožňuje stanovit nejvýše 100 stavových proměnných.
• Účelová funkce (Objective function – Obj) – je funkce, nebo hodnota, která je výsledkem optimalizačního procesu. Může být stanovena pouze 1 účelová funkce. Postup provádění optimalizační analýzy je znázorněn na obr. 1. Nejdříve se vyšetří návrhový prostor obr. 2, tj. prostor, který je definován limitními hodnotami jednotlivých proměnných. Lze ho vyšetřit optimalizačními nástroji, jako například Single Loop, Random, Sweep, Gradient, Factorial. Ty slouží k rozpoznání optimalizačního prostředí a upřesnění hranic kolem hledaného optima funkce.
• Single Loop – vykoná jeden optimalizační cyklus. Vhodné pro ověření správnosti nastavení hodnot proměnných.
• Random – generuje náhodné návrhy přiřazením náhodných hodnot do návrhových proměnných. Užitečné pro počáteční návrh před spuštěním samotné optimalizace. Udává představu o tvaru účelové funkce.
• Sweep – rozmítání proměnných po celém intervalu každé návrhové proměnné. Vhodné pro představu, jak se funkce chová při změnách návrhových proměnných.
• Gradient – mění hodnoty návrhových proměnných malou hodnotou a zjišťuje tvar funkce v okolí bodu. Vhodné pro zpřesnění výpočtu a vyvarování se dosažení lokálního extrému. Tento nástroj je automaticky používán na konci každého návrhu, řešeného metodou iterace podprostoru.
• Factorial – Stanovuje hranice návrhového prostoru z mezních hodnot návrhových proměnných. Užitečné pro představu chování funkce při změně jedné i více návrhových proměnných. Upřesnění, resp. snížení rozsahu intervalu proměnných a poznání prostředí kolem hledaného optima mohou zamezit problémům s příp. divergencí řešení, nebo „uvíznutím“ v lokálním extrému funkce. Poté je nutné zvolit jednotlivé proměnné a jejich vhodné limitní hodnoty a stanovit účelovou funkci.

Obr. 5a – Oboustranně pevně uložený


Obr. 5b – Prostě uložený

KONSTRUKČNÍ OPTIMALIZACE TAŽENÉ KONZOLY
Geometrie v prvotním návrhu je představena délkou l = 10 m, výškou konzoly ve vetknutí h1 = 0,2 m, ve středu délky h2 = 0,2 m a na volném konci h3 = 0,1 m. Stavová proměnná je dána horním omezením napětí 30 MPa. Návrhová proměnná spočívá v toleranci výšky ve středu konzoly h2 od 0,15 do 0,27 m a účelovou funkcí je objem prvku. Příklad byl řešen metodou podprostoru aproximace.
Ke konvergenci bylo zapotřebí 7 optimalizačních cyklů. Obr. 2 ukazuje hodnoty výsledků v návrhové oblasti pro jednotlivé optimalizační cykly 1 – 7 (obr. 3). Z nich byl jeden nepřípustný (infeasible), neboť nevyhověl nejméně jedné z podmínek. Z obr. 2 je zřejmé, že se jedná o č. 3, který nevyhověl omezení stavové proměnné. Ostatní hodnoty jsou přípustné (feasible). Sada výsledků, která nejlépe vystihuje cíle úlohy je č. 7. Vyhovuje všem daným podmínkám a zároveň dosahuje nejnižší hodnoty účelové funkce. Na obr. 3 je optimalizovaná konzola odpovídající sadě výsledků č. 7.

Obr. 4 – Model stěny

TOPOLOGICKÁ OPTIMALIZACE
(TOPOLOGICAL OPTIMIZATION)
Topologická optimalizace představuje malou, ale rychle se rozvíjející oblast výpočetní mechaniky. Jedná se o tvarovou optimalizaci, snažící se o stanovení nejlepšího využití materiálu po průřezu navrhovaného prvku. Na rozdíl od návrhové optimalizace, topologická nevyžaduje přesné definování optimalizačních parametrů (tj. návrhové proměnné). Optimalizačním parametrem v této analýze je materiálová funkce, tedy rozložení materiálu po ploše, či objemu prvku.
Cílem topologické optimalizace je maximalizovaná, nebo minimalizovaná účelová funkce (maximalizace vlastních frekvencí, minimalizování poddajnosti konstrukce atd.), po vyřešení a splnění všech zadaných podmínek (redukce objemu atd.). Návrhové proměnné jsou v tomto řešení stanovené jako pseudo-hustoty, které jsou přiřazené každému konečnému prvku. Tato metoda je vhodná pro představu využití materiálu po prvku tak, aby byla maximalizována jeho tuhost.

Obr. 6 – Model prostorového prvku

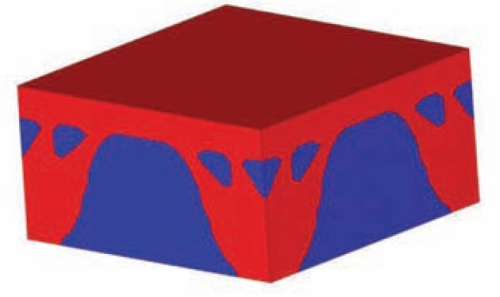
Obr. 7a – Vykreslení důležitosti materiálu


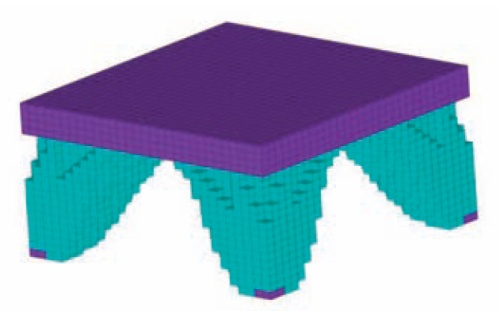
Obr. 7b – Optimalizovaný tvar konstrukce

POSTUP ŘEŠENÍ
Postup řešení je obdobný jako u jiných analýz prováděných metodou konečných prvků.

• Na rozdíl od předchozí návrhové optimalizace, topologická umožňuje při tvorbě modelu používat GUI příkazů v uživatelském prostředí Ansysu. Nejprve je nutné stanovit geometrii modelu a materiálové vlastnosti. Musí být defi nován Youngův modul, Poissonovo číslo, popř. hustota materiálu (pokud uvažujeme vlastní tíhu konstrukce). Dále zatěžovací stav, ať už jeden, či více. Po stanovení všech těchto parametrů, je nutné zvolit správný výběr prvku.
• Ansys umožňuje řešit topologickou optimalizaci pomocí pěti prvků, kterými jsou: Tabulka 1 – Typy prvků pro řešení Topologické optimalizace systémem ANSYS 2D modely PLANE82 PLANE183 3D modely SOLID92 SOLID95 skořepiny SHELL93 kde PLANE82 je 2-D 8-uzlový prvek, PLANE183 je 2-D 8-uzlový prvek, nebo 6-uzlový prvek, SOLID92 je 3-D 10-uzlový prvek, SOLID95 je 3-D 20-uzlový prvek a SHELL93 je skořepinový 8-uzlový prvek.
• Následuje stanovení optimalizované a neoptimalizované návrhové oblasti. Tj. určit oblast, kde chceme provést topologickou optimalizaci. Ansys umožňuje provést optimalizaci jen na prvku označeném číslem 1. Z toho tedy vyplývá, že v oblasti, kterou chceme podrobit topologické optimalizaci, volíme prvky 1 a oblasti, jež jsou součástí konstrukce, ale optimalizovány nebudou, budou vytvořeny prvky 2 a více.
• Stanovení zatížení a zatěžovacích stavů. Topologickou optimalizaci lze provést pro jeden i více zatěžovacích stavů.
• Dalším krokem je nastavení řešiče (stanovení konečného počtu iterací, požadovanou redukci materiálu) a provedení výpočtu.
• Posledním krokem je vyhodnocení výsledků. Tzn. rozhodnout, zda provedený návrh je vhodným výsledkem pro naše řešení.

TOPOLOGICKÁ OPTIMALIZACE ROVINNÉ STĚNY
Dále bude demonstrována topologická optimalizace rovinné stěny vytvořené prvky PLANE82, v prvním případě podepřené v dolních rozích neposuvnými klouby a ve druhém případě bude jeden z rohů osazen kloubem umožňující vodorovný posun. Rozměry jsou: délka l = 10 m, výška h = 5 m a šířka 0,4 m (obr. 4). Model lze vytvořit GUI příkazy uživatelského prostředí, nebo využít ANSYS příkazů v dávkovém souboru. Stěna je zatížena na horní linii hodnotou q = 10 kN/m. U obou příkladů se předpokládá neměnný materiál 0,8 m pod zatížením. Tzn., že prvky v této oblasti nebudou podrobeny procesu optimalizace. Materiálové charakteristiky odpovídají betonu B20. V řešiči je nastaven max. počet iterací 100, avšak výpočet je ukončen po dosažení konvergence. Redukce materiálu, v obou případech, je volena 70 %.
Na obr. 5a a 5b jsou výsledky řešení topologické optimalizace stěny (popsané výše). U vykreslení výsledků jsou voleny 2 kontury představující důležitost materiálu, kde červená představuje nutný materiál pro dosažení maximální tuhosti konstrukce při ztrátě 70 % objemu, přičemž modrá znázorňuje materiál s malým vlivem pro její tuhost. Při prostém podepření dostáváme táhlo podél spodní linie stěny, což je způsobeno právě možností posunutí v místě podepření posuvným kloubem. Tvar materiálu potřebného pro tuhost konstrukce odpovídá představě o příhradové analogii užívanou při vyztužování stěnových betonových prvků. Tento postup (topologická optimalizace) lze tedy s výhodou využít pro stanovení oblastí, jež je nutno vyztužit pro dostatečnou tuhost betonových stěnových konstrukcí a také pro představu vhodného tvaru konstrukce za daných okrajových podmínek. Dále bude tento proces demonstrován na prostorovém prvku.

TOPOLOGICKÁ OPTIMALIZACE PROSTOROVÉHO PRVKU
Tato úloha představuje řešení topologické optimalizace prostorového kvádru s čtvercovým půdorysem vytvořeného prvky SOLID92. Rozměry odpovídají předchozímu příkladu. Tj. délka = šířka = 10 m, výška h = 5 m. Je podepřen ve spodních rozích pevnými neposuvnými klouby. Obr. 6 znázorňuje zadání příkladu bez zatížení a okrajových podmínek. Fialová barva představuje část tělesa, která není určena k optimalizování. Např. se může jednat o část, jež má podstatný význam z konstrukčního hlediska. Na obr. 7a je vykreslení důležitosti materiálu, obdobně jako v předchozím příkladu, dvěma konturami. Obr. 7b ukazuje výsledky po dosažení optimálního tvaru využití materiálu po odstranění prvků, jejichž přítomnost se, za daného objemu, považuje za méně podstatnou pro tuhost konstrukce.

ZÁVĚR
Design Optimization a Topological Optimization jsou samostatné moduly implementované v konečněprvkovém systému ANSYS umožňující řešení optimalizačních problémů. V oblasti stavebních konstrukcí se nejedná o optimalizaci z hlediska Matematického operačního výzkumu, ale spíše o využití těchto postupů k dosažení efektivnějšího návrhu.
Design Optimization je možné s výhodou využít při konstrukčním výpočtu, kde lze kontrolovat překročení limitních hodnot proměnných a dosáhnout tím efektivnějšího návrhu konstrukce. Nabízí širokou škálu využití v mnoha inženýrských oblastech. Topological Optimization je optimalizační modul, kterým jsme schopni získat značnou úsporu materiálu představou o optimálním tvaru konstrukce. Je vhodný zejména v prvotním návrhu, nebo při řešení betonových konstrukcí pro stanovení nejefektivnějšího využití výztuže.

Příspěvek vznikl za podpory projektu MSM0021630519 a projektu GAČR 103/08/0275.

Autor

• Ing. Fedorik Filip