Možnosti využití CFD analýzy ve stavebnictví

Jedním z nejčastějších klimatických zatížení, které působí na stavební konstrukce, je zatížení větrem. Účinky tohoto zatížení je nutné vždy zahrnout do statického výpočtu obzvlášť, jedná-li se o lehké stavební konstrukce. Do této kategorie spadají i textilní membránové konstrukce. Jedná se o konstrukce, jejíž hlavním prvkem je textilní membrána, která je napnuta za pomocí ocelové respektive lanové konstrukce. Takovýmto způsobem lze dosáhnout zastřešení velkých rozponů a současně zajistit elegantní a nevšední vzhled díla.

V tomto příspěvku je pojednáno o analýze vzdušného proudění v okolí jednoduché membránové konstrukce. Jedná se o zborcenou plochu tvaru hyperbolického paraboloidu. U konstrukcí takovýchto tvarů je velmi obtížné stanovit hodnoty zatížení od působícího větrného proudění, jelikož tvarové uspořádání těchto konstrukcí není uváděno v normách. Pokud chceme podrobněji popsat účinky větrného proudění u tvarově složitějších konstrukcí, je třeba využít experimentálních simulací ve větrném tunelu nebo numerických simulací na výpočetních stanicích. V předloženém příspěvku je popsána druhá z možností.

Pro analýzu byly vybrány čtyři varianty tvaru hyperbolického paraboloidu se shodným půdorysem avšak s rozdílným zakřivením membrán. Byl sledován vliv změny rychlosti proudění a vliv změny zakřivení membrány pro různé směry proudění na konstrukci. Před samotnou analýzou byla však nejdříve provedena srovnávací studie přístřešku, pro něž lze hodnoty zatížení větrem nalézt v normě. [5] Výpočty byly provedeny za použití softwaru ANSYS/CFX. [4]

SROVNÁVACÍ STUDIE 
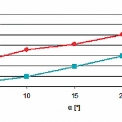
Před samotnou analýzou bylo nezbytné provést ověření metodiky výpočtu, aby bylo možné považovat získaná data za věrohodné. Pro toto ověření byl zvolen přístřešek, jehož střešní plocha je situována do tvaru nakloněné roviny. Tento případ byl zvolen proto, že hodnoty součinitelů tlakového zatížení Cp jsou pouze pro takovýto přístřešek popsány v normách. Výsledky z CFD analýzy tohoto přístřešku byly konfrontovány s výsledky výpočtu za pomocí norem a bylo dosaženo předpokladů, že hodnoty tlaků určených pomocí norem jsou vyšší než hodnoty určené CFD analýzou (obr. 1). Podrobněji je srovnávací studie popsána v [2].

VÝPOČTOVÝ MODEL 
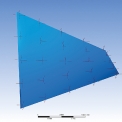
Pro analýzu membránové konstrukce byla zvolena jedna z častých variant, kterou lze označit jako bodová plachta. Membrána je tvaru zborcené plochy, konkrétně je předepsána plochou hyperbolického paraboloidu. Půdorysné rozložení membrány je 2 × 2 m. Zakřivení membrány je symetrické podle úhlopříček půdorysu konstrukce, tj. protilehlé body jsou ve shodné výšce. Byly zvoleny celkem čtyři varianty zakřivení a to tak, že jedna dvojce úhlopříčně protilehlých koncových bodů byla ve výšce 2 m a výška druhé dvojice byla postupně nastavena na hodnoty {2,25; 2,50; 2,75; 3,00} m. Varianty jsou označeny A, B, C, D, podle předchozí posloupnosti. Dále byly zvoleny celkem tři varianty směru proudění vzduchu. První proudění (označený jako skupina I) bylo nastaveno ve směru rovnoběžném s půdorysnými hranami membrány. Další proudění (skupina II) probíhalo v diagonálním směru mezi koncovými body membrány, které se nacházejí ve výšce 2,00 m a poslední směr proudění (skupina III) byl situován v druhém diagonálním směru, tj. diagonála s postupně upravovanými koncovými body. Situace je naznačena na obrázku 2.

NASTAVENÍ PARAMETRŮ VÝPOČTU 
Úloha byla uvažována jako transientní s proměnnou délkou časového kroku. Časový krok byl nastaven dle rychlosti proudění a snižován v průběhu simulace uživatelem tak, aby se maximální dosažená hodnota Courantova čísla nacházela v rozmezí 1 – 5 pro danou oblast vzdušného proudění. Médium, které vyplňovalo oblast v okolí konstrukce, bylo uvažováno s charakteristiky vzduchu při teplotě 25 °C. Za zmínku stojí pak hustota ρ = 1,185 kgm^–3 a dynamická viskozita μ = 1,831 × 10⁵ kgm^–1s^–1.

Okrajové podmínky na vstupu byly definovány proměnnou rychlostí proudění dle rovnice (1) a to tak, aby ve výšce, odpovídající výšce přístřešku, byly dosaženy rychlosti proudění tekutiny v = {1, 5, 10, 15, 20, 25, 30} ms^–1. Na výstupu pak byla definována nulová hodnota relativního tlaku p = 0 Pa. Horní a zbylé dvě boční stěny měly zadánu podmínku tzv. volného proudění, tzn. složka rychlosti proudění kolmá na rovinu okraje je rovna nule. Pro spodní stěnu modelu a konstrukci přístřešku byla zvolena stěnová okrajová podmínka.

kde: vx – je rychlost na vstupu; v_norm – rychlost větru ve normativní výšce (výška konstrukce); h – výška; h_norm – normativní výška; α – součinitel expozice [8].

Pro tato nastavení odpovídá Reynoldsovo číslo hodnotám R_e = 3 × 10⁴ a vyšší, úloha se tedy nachází v oblasti turbulentního proudění. Proto byl pro výpočet použit turbulentní model proudění, konkrétně model k-ε. Tekutina byla uvažována jako nestlačitelná a nebyl uvažován přenos tepla.

ANALÝZA VÝSLEDKŮ 
Pro každou z variant bylo primárně sledováno tlakového pole na povrchu membrány. Během průběhu simulace nedocházelo v okolí membrány ke vzniku výrazných fluktuací. Na povrchu membrány bylo určeno 50 bodů (25 na horní stěně a 25 na dolní stěně) a v těchto bodech bylo získáno tlakové zatížení. Následně byly tyto hodnoty sečteny (respektive odečteny, jelikož kladný směr normálových os obou stěn membrány je opačný) pro odpovídající si horní a spodní body povrchu membrány a následně porovnány. Rozložení bodů je patrné z obrázku 3.

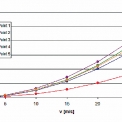
Během analýzy byly sledovány jevy, které by mohli ovlivnit chování tlakového pole. Prvním ze sledovaných vlivů byl vliv rychlosti proudění na hodnoty tlaků na povrchu membrány. Závislost hodnot tlakového pole byla ve všech bodech shodná, hodnoty tlaků rostly s druhou mocninou rychlosti tak, jak je předpokládáno (obr. 4).

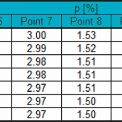
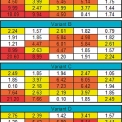
Dalším ze sledovaných vlivů byl ten, zda nárůst rychlosti nezpůsobí redistribuci tlakového pole. K tomuto účelu byly sečteny absolutní hodnoty tlaků na konstrukci a k tomuto součtu určeny procentuelní poměry hodnot tlaků v daných bodech příslušných variant. I zde se potvrdil předpoklad, že změna rychlosti nezpůsobí výraznou redistribuci tlakového pole. Hodnoty pro 5 vybraných bodů jsou uvedeny níže (obr. 6).

Třetí ze sledovaných vlivů byl vliv zakřivení membrány. Vzhledem k tomu, že rychlost proudění neměla vliv na redistribuci tlakového zatížení, bylo pro sledování vlivu zakřivení použito poměrné rozdělení tlaků na membráně. U všech tří variant směru proudění větru docházelo se zvyšujícím se zakřivení k úbytku zatížení za návětrnou hranou a k jeho přesunu a koncentraci ve střední části membrány. Zde se zatížení redistribuovalo ve směru kolmém na směr proudění. Pro ilustraci je redistribuce zatížení zobrazena na obrázku 7.

ZÁVĚR 
V rámci projektu specifického výzkumu FAST‑J‑11‑35 byla provedena jedna z alternativních možností výpočtu zatížení větrem na atypické konstrukci, která není explicitně obsažena v normách. Pro uváděnou CFD analýzu bylo sestaveno několik variant modelů membránové konstrukce a zde prezentované výsledky jsou v dobré shodě s všeobecnými předpoklady. Je třeba však podotknout, že vzhledem k nízké tuhosti textilních membránových konstrukcí, může dojít během působení větru k deformaci konstrukce a tím i následně ke změně proudění v jejím okolí, což může mít za následek změnu tlakového pole na membráně. Proto se pro hlubší studium tohoto chování jeví jako vhodné využít nástroje Fluid-structure interaction (FSI), který kombinuje výpočet proudění s pevnostním výpočtem.

Tento článek vznikl za finančního přispění projektu GAČR 104/11/0703 a projektu specifického výzkumu FAST‑J‑11‑35.

LITERATURA: 
[1] KRIŽAN, J. Analýza konstrukcí v interakci se vzdušným proudem. Teze doktorské disertační práce. Vysoké učení technické v Brně. Fakulta stavební. Ústav stavební mechaniky. 2011. 25 s.
[2] KRIŽAN, J. CFD analýza membránové konstrukce. Juniorstav 2012, VUT v Brně, Fakulta stavební. Brno, 2012, 7 stran, ISBN 978-80-214-4393-8
[3] RIZZO, F., D’ASDIA, P., LAZZARI, M., PROCINO, L., 2011. Wind action on tension roofs of hyperbolic paraboloid shape. Engineering Structures 33 (2011) 445–461
[4] ANSYS CFX, Release 12.1
[5] EUROCODE 1 – EN 1991–1–4
[6] VERSTEEG,, H. K.; MALALASEKERA, W. An Introduction to Computational Fluid Dynamics. The Finite Volume Method. Essex: Longman Scientific & Technical. 1995. 257 str. ISBN 0-582-21884-5
[7] ZHANG, A., GU, M., Wind tunnel tests and numerical simulations of wind pressures on buildings in staggered arrangement. Journal of Wind Engineering and Industrial Aerodynamics 96 (2008) 2067–2079
[8] HIRNŠAL, Z., Textilní architektura. Časopis Fasády, MISE s.r.o., Leden 2005

Possibilities for the Use of CFD Analysis in Civil Engineering
In construction practice we encounter structures whose wind load is very difficult to determine due to their shape design. Thus, there occurs a problem for engineers to determine properly the course of load for such a structure. One of the possibilities which become more actual thanks to the development of new technologies is numeric simulation of wind flow named CFD (Computational Fluid Dynamics).

Autor

• Ing. Křižan Jiří