Projektování
Projektování  K možnostem použití rovnoramenných úhelníků z ocelí S450J0 a S460M v ocelových příhradových konstrukcích
K možnostem použití rovnoramenných úhelníků z ocelí S450J0 a S460M v ocelových příhradových konstrukcíchK možnostem použití rovnoramenných úhelníků z ocelí S450J0 a S460M v ocelových příhradových konstrukcích
Rubrika: Projektování
Článek se zabývá problematikou navrhování a posuzování tlačených prvků ocelových příhradových konstrukcí. Pozornost je zaměřena především na návrh nárožníků z rovnoramenných úhelníků u ocelových příhradových stožárů. V článku jsou vyhodnoceny možnosti uplatnitelnosti ocelí jakostních tříd S450J0 a S460M.
Rovnoramenné úhelníky se používají jako běžný konstrukční prvek při návrhu ocelových příhradových stožárů. Tento typ konstrukcí se uplatňuje především v energetice jako stožáry přenosových soustav či nosné konstrukce větrných elektráren, viz obrázek 1. Většina realizovaných konstrukcí je navržena z tradičních ocelí pevnostních tříd S235 či S355.
Vývoj v oblasti hutních technologií umožňuje výrobcům hutního materiálu zavádět produkci dalších typů konstrukčních ocelí se zvýšenou přidanou hodnotou oproti tradičním ocelím pevnostních tříd S235 a S355. Jedním z nově zaváděných výrobků společnosti ArcelorMittal jsou rovnoramenné úhelníky z ocelí S450J0 a S460M.
Výhody použití výšepevných ocelí S450J0 a S460M při návrhu příhradových konstrukcí se nejvíce projeví při návrhu prvků namáhaných na tah. Pro návrh nárožníků [1] a často také prvků ztužení [2] je však obvykle rozhodující posudek tlačeného prutu na vzpěr. Do výpočtu návrhové vzpěrné únosnosti tlačeného prutu z rovnoramenného
úhelníku vstupuje větší množství veličin, jako například vzpěrné délky, průřezové charakteristiky úhelníků a hodnota meze kluzu oceli.
Aby bylo možno vyhodnotit ekonomickou efektivitu použití ocelí S450J0 a S460M, bylo potřebné provést srovnávací parametrickou studii, v rámci které byly pro různé návrhové situace (definované návrhovou hodnotou normálové síly v nárožníku NEd a vzpěrnou délkou pro příslušný způsob vybočení) navrženy ekonomicky nejvýhodnější profily z různých pevnostních tříd ocelí. Pro návrh ekomomicky nejvýhodnějších profilů byla vytvořena jednoduchá softwarová aplikace.
VZTAH MEZI VZPĚRNOU DÉLKOU A JAKOSTÍ KONSTRUKČNÍ OCELI
Vzpěrná délka L vstupuje do výpočtu vzpěrné únosnosti Nb,Rd ve vztahu (1) pro výpočet štíhlosti prvku m:
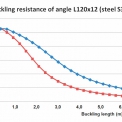
Je potřeba rozlišovat vzpěr kolmo k ose y-y a vzpěr kolmo k ose v-v. Je zřejmé, že se zvyšující se hodnotou vzpěrné délky L se lineárně zvyšuje také hodnota štíhlosti prvku λ a klesá výsledná vzpěrná únosnost Nb,Rd. Grafická závislost mezi vzpěrnou délkou L, vzpěrnou únosností Nb,Rd a způsobem vybočení je pro vybraný rovnoramenný úhelník L120×12 z oceli S355 znázorněna na obrázku 2 (zpracováno pro křivku vzpěrné pevnosti b).
Jakost oceli, vyjádřená jmenovitou hodnotou meze kluzu fy, ovlivňuje výpočet vzpěrné únosnosti Nb,Rd v následujících částech výpočetní procedury:
a) ve vztahu pro výpočet Nb,Rd:
b) ve vztahu pro výpočet štíhlosti λ1: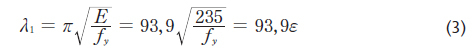
c) ve vztahu, který rozhoduje o potřebě redukce průřezové plochy u úhelníků zatříděných jako průřez třídy 4 (podrobnosti jsou uvedeny v části 4.4 normy ČSN EN 1993-1-5):
Ze vztahu (2) vyplývá, žeúnosnost centricky tlačeného prutu (bez vlivu vzpěru a boulení od normálových napětí) je přímo úměrná jmenovité hodnotě meze kluzu oceli fy. Pokud se zvolí za referenční hodnotu jmenovitá mez kluzu oceli S355 (odpovídá 100 %), pak lze vyčíslit maximální procentuální přírůstky či úbytky únosností zvoleného průřezu při použití jiných typů ocelí:
- ocel S235: 66,2 %
- ocel S355: 100,0 %
- ocel S420: 118,3 %
- ocel S450: 126,8 %
- ocel S460: 129,6 %
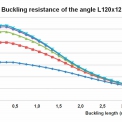
Ze vztahu (3) pro výpočet štíhlosti λ1 vyplývá, že oceli s vyšší jmenovitou hodnotou meze kluzu fy jsou více citlivé na účinky vzpěru. Profil s vyšší hodnotou meze kluzu fy vykazuje při stejné vzpěrné délce L (či štíhlosti λ) vyšší hodnotu poměrné štíhlosti λ a tím i nižší hodnotu součinitele vzpěrnosti χ než stejný profil s nižší hodnotou meze kluzu oceli. Grafická závislost mezi vzpěrnou délkou L, vzpěrnou únosností Nb,Rd a jakostní třídou oceli je pro vybraný rovnoramenný úhelník L120×12 zobrazena na obrázku 3 (uvažuje se vzpěr kolmo k ose v-v a křivka vzpěrné pevnosti “b“). Vyšší hodnoty poměrné štíhlosti λ při stejném profilu a totožné vzpěrné délce se u ocelí vyšších pevností projevují ve větším sklonu křivek uvedených na obrázku 3.
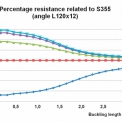
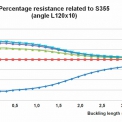
Procentuální porovnání vzpěrných únosností pro výše uvedený případ je znázorněno na obrázku 4. Z obrázku vyplývá, že efektivní použití úhelníků z výšepevných ocelí lze očekávat především u prutů méně náchylných na účinky vzpěru.
Ze vztahu (4), který rozhoduje o potřebě redukce průřezové plochy, vyplývá, že úhelníky navržené z ocelí s vyšší hodnotou meze kluzu jsou obecně více citlivé na možné účinky boulení stěn od normálových napětí. Problematiku lze demonstrovat na příkladu tlačených prutů z rovnoramenného úhelníku L120×10. V tabulce 1 jsou uvedeny hodnoty štíhlosti λp určené podle vztahu (4) a hodnoty účinné plochy Aeff odpovídající různým pevnostním třídám oceli (výpočet λp vycházel z konzervativního předpokladu b = h).
| Tabulka 1 – Účinná plocha rovnoramenného úhelníku L120×10 | ||||
| rovnoramenný úhelník L120x10 | ||||
| ocel |
průřezová plocha A |
štíhlost |
účinná plocha Aeff |
poměr Aeff /A |
| S235 | 2 320 | 0,644 | 2 320 | 100% |
| S355 | 0,792 | 2 231 | 96,2% | |
| S420 | 0,861 | 2 098 | 90,4% | |
| S450 | 0,892 | 2 044 | 88,1% | |
| S460 | 0,902 | 2 027 | 87,3% | |
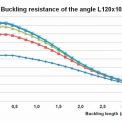
Grafické závislosti mezi vzpěrnou délkou L a vzpěrnou únosností Nb,Rd tlačených prutů z rovnoramenného úhelníku L120×10 jsou obdobně jako pro tlačené pruty z rovnoramenného úhelníku L120×12 (viz obrázky 3 a 4) znázorněny na obrázcích 5 a 6. Vliv boulení se u ocelí s vyšší hodnotou meze kluzu fy projevuje snížením rozdílů mezi vzpěrnou únosností ocelí různých pevnostních tříd. Efektivnost použití výšepevných ocelí se tak u profilů náchylných k účinkům boulení od normálových napětí snižuje.
VLIV PRŮŘEZOVÝCH CHARAKTERISTIK
Při výpočtu vzpěrné únosnosti tlačeného prutu z rovnoramenného úhelníku vstupují do výpočtu následující průřezové charakteristiky:
a) tloušťka příruby t
b) šířka příruby b
c) průřezová plocha A
d) poloměr setrvačnosti (iy nebo iv)
Tloušťka příruby t a šířka příruby b mají vliv na výpočet účinné plochy průřezu Aeff, viz rovnice (4). Průřezy s větším vzájemným poměrem b/t jsou více citlivé na účinky boulení.
Poloměr setrvačnosti (iy nebo iv) vstupuje do výpočtu štíhlosti prvku podle vztahu (1). Se zvyšující se hodnotou poloměru setrvačnosti průřezu klesá jeho citlivost na účinky vzpěru. Při porovnání dvou průřezů se stejnou (nebo velmi blízkou) průřezovou plochou vykazuje průřez s širší tenčí přírubou větší hodnotu poloměru setrvačnosti
ve srovnání s průřezem s užší tlustší přírubou. Požadavek na maximalizaci hodnoty poloměru setrvačnosti je tak v rozporu s požadavkem na omezení štíhlosti přečnívající tlačené části s ohledem na účinky boulení od normálových napětí.
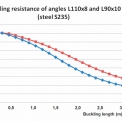
Vliv výše uvedených průřezových charakteristik lze demonstrovat na příkladu porovnávajícím vzpěrnou únosnost prutů z rovnoramenných úhelníků L110×8 a L90×10. Oba průřezy mají stejnou průřezovou plochu A = 1 710 mm2. Poloměr setrvačnosti průřezu L110×8 je iv = 21,8 mm, poloměr setrvačnosti průřezu L90×10 je iv = 17,6 mm. Analýza je zpracována pro dvě pevnostní třídy oceli – S235 a S460. Grafická závislost mezi vzpěrnou délkou L, vzpěrnou únosností Nb,Rd a jakostní třídou oceli je pro výše uvedené rovnoramenné úhelníky zobrazena na obrázcích 7 a 8 (uvažuje se vzpěr kolmo k ose v-v a křivka vzpěrné pevnosti “b“).
Účinná plocha Aeff obou profilů z oceli S235 odpovídá průřezové ploše A = 1 710 mm2, vliv boulení od normálového napětí se neuplatní. Při výpočtu vzpěrné únosnosti se plně uplatní příznivý efekt vyšší hodnoty poloměru setrvačnosti u průřezu z rovnoramenného úhelníku L110×8, viz obrázek 7.
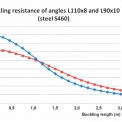
Při použití oceli S460 je účinná plocha průřezu z rovnoramenného úhelníku L110×8 rovna Aeff = 1 343,7 mm2, u průřezu z rovnoramenného úhelníku L90×8 je účinná plocha rovna průřezové ploše Aeff = A = 1 710 mm2. Z obrázku 8 vyplývá, že vliv boulení od normálového napětí se projeví u prutů s menší vzpěrnou délkou, u prutů s větší vzpěrnou délkou převažuje vliv rozdílných hodnot poloměru setrvačnosti iv.
CENA HUTNÍHO MATERIÁLU
Cena, vztažená k jednotce hmotnosti konkrétního profilu, je jedním z rozhodujících parametrů ovlivňujících uplatnitelnost různých jakostních tříd oceli. Cena je však, na rozdíl od dalších vstupních parametrů ovlivňujících efektivitu použití konkrétního konstrukčního prvku z příslušné jakostní třídy oceli (průřezové charakteristiky, mez kluzu oceli, vzpěrné délky), výrazně proměnnou veličinou. Cena za konkrétní profil je závislá na mnoha parametrech, které lze zjednodušeně rozdělit do dvou základních skupin:
a) systematické parametry,
b) tržní parametry.
Popis tržních parametrů (cena vstupních surovin, výrobní náklady, obchodní strategie výrobců a prodejců hutního materiálu, vývoj trhu atp.), které určují konkrétní cenové hladiny, výrazně přesahuje rozsah této studie. V dalším textu jsou proto stručně popsány pouze hlavní systematické parametry, pomocí kterých se definuje procedura výpočtu ceny konkrétního profilu. Při výpočtu ceny za konkrétní profil se obvykle postupuje podle následující procedury:
CENA = ZÁKLADNÍ CENA + PŘÍDAVKY (P1, P2 …, Pi) (5)
Základní cena je obvykle vztažena k šířce příruby rovnoramenného úhelníku. Speciální přídavky mohou zohledňovat:
- jakost použité oceli,
- nestandardní délku prvku,
- speciální požadavky na ověření vlastností materiálu,
- finální úpravy produktu (značení, způsob balení, rovnání atp.),
- objednané množství produktu,
- další parametry (např. uskladnění objednaného zboží).
Ve srovnávací studii uvedené v tomto článku jsou použity ceny odvozené z oficiálního cenového katalogu společnosti ArcelorMittal (ceny platné k 1. 12. 2013). Takto nastavený systém cen se používá pro trh v Německu a ve Francii.
Základní cena se vztahuje k šířce přírub rovnoramenných úhelníků, které jsou pro tento účel rozděleny do 4 kategorií AM1 až AM4, viz tabulka 2. Hodnoty přídavků za jakost oceli jsou uvedeny v tabulce 3.
| Tabulka 2 – Základní ceny rovnoramenných úhelníků | ||
| kategorie | velikosti | základní cena |
| AM1 | L20 až L140 | 450 €/t |
| AM2 | L150 | 500 €/t |
| AM3 | L160 až L200 | 500 €/t |
| AM4 | L250 až L300 | 500 €/t |
| Tabulka 3 – Přídavky za jakost oceli | |
| jakost oceli | přídavek na jakost |
| S235JR | 0 €/t |
| S235J0 | 0 €/t |
| S355JR | 35 €/t |
| S355J0 | 40 €/t |
| S355J2 | 50 €/t |
| S355K2 | 60 €/t |
| S420M | 100 €/t |
| S450J0 | 80 €/t |
| S460M | 100 €/t |
STUDIE UPLATNITELNOSTI VÝŠEPEVNÝCH OCELÍ
Při návrhu nosných profilů nárožníků příhradových stožárů se musí projektant vypořádat s typickou návrhovou situací, kdy zná návrhovou hodnotu tlakové síly v prvku NEd (stanovená na základě globální analýzy konstrukce) a má určeny příslušné vzpěrné délky (vyplývají z konstrukčního řešení příhradového stožáru).
Aby bylo možné získat zobecněné informace o vhodnosti a efektivnosti použití výšepevných ocelí pro nárožníky příhradových stožárů, bylo potřeba provést parametrickou srovnávací studii, při které byla sledována závislost mezi:
- návrhovou hodnotou tlakové síly v nárožníku NEd,
- vzpěrnou délkou L,
- nejvíce ekonomicky efektivním návrhem profilu z konkrétní třídy oceli (nemusí se nutně jednat o vyhovující profil s nejnižší hmotností).
Parametrická studie, jejíž výsledky jsou uvedeny v této kapitole, byla provedena s využitím Software pro optimalizaci návrhu tlačených prutů z rovnoramenných úhelníků [6]. V rámci studie byl pro různé návrhové situace definované hodnotlou tlakové síly v prvku NEd a vzpěrnou délkou prvku Lv-v stanoven ekonomicky nejvýhodnější profil z konkrétní jakostní třídy oceli. U všech profilů odpovídajících konkrétní návrhové situaci byl stanoven procentuální rozdíl ceny vztažený k ceně oceli pevnostní třídy S355. Získané diskrétní hodnoty byly zobecněny a vyhodnoceny s využitím regresní analýzy. Studie vycházela z následujících postupů a předpokladů:
- Uvažoval se vzpěr kolmo k ose v-v.
- Byla použita křivka vzpěrnosti “b“.
- Vzpěrné délky Lv-v se uvažovaly v rozmezí 0 mm až 3 000 mm s odstupňováním po 500 mm.
- Návrhové hodnoty tlakové síly NEd se uvažovaly v rozmezí 250 kN až 5 000 kN s odstupňováním po 250 kN.
- Studie pracovala s jakostmi oceli S235J0, S355J0, S420M, S450J0, S460M.
- Ceny za materiál odpovídaly hodnotám uvedeným v tab. 2 a 3.
- Studie nezohledňuje navýšení výrobních nákladů při použití výšepevných ocelí.
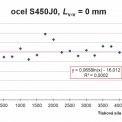
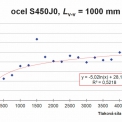
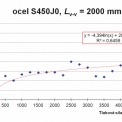
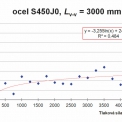
Grafické znázornění výsledků parametrické studie je patrné z obrázků 9 až 12 (na obrázcích jsou uvedeny pouze výsledky pro ocel S450J0, výsledky pro ocel S460M jsou obdobné). Z uvedených výsledků vyplývají následující zjištění:
a) Podle očekávání se výšepevné oceli nejvíce efektivně uplatňují při návrhových situacích s malým vlivem vzpěru.
b) Pro zadané cenové hladiny lze při použití obou ocelí S450J0 i S460M dosáhnout maximální ekonomické úspory cca 15,5 % (návrhová situace bez uplatnění vzpěru). Uvedená ekonomická úspora odpovídá průměrné hodnotě, viz obrázek 9 a tabulka 4.
c) Nastavení cen pro ocel S420M je z hlediska uplatnění této oceli nevýhodné.
d) Ze studie vyplává, že uplatnění oceli S235J0 je v běžných návrhových situacích značně neekonomické v porovnání s dalšími jakostními třídami ocelí.
e) Pro možnost porovnání byly, kromě cenově nejvýchodnějších profilů, hledány také vyhovující profily s minimální hmotností. Ze studie vyplývá, že hmotnostně optimální profil z konkrétní třídy oceli nemusí být nutně profilem cenově nejvýhodnějším.
| Tabulka 4 – Rozdíl cen vztažený k S355J0 (Lv-v = 0 mm) | |||||||
| Rozdíl cen vztažený k S355J0 (%) | |||||||
| Lcr = | 0 | mm | Jakost oceli | ||||
| Síla v nárožníku | S235J0 | S355J0 | S420M | S450J0 | S460M | ||
| N = | 250 | kN | 32,1 | 0,0 | -4,5 | -16,9 | -13,8 |
| N = | 500 | kN | 47,3 | -4,0 | -12,4 | -12,8 | |
| N = | 750 | kN | 40,5 | -0,6 | -12,7 | -9,4 | |
| N = | 1 000 | kN | 48,7 | -4,7 | -17,0 | -13,9 | |
| N = | 1 250 | kN | 59,4 | -0,8 | -11,3 | -14,3 | |
| N = | 1 500 | kN | 72,2 | -4,6 | -13,6 | -10,3 | |
| N = | 1 750 | kN | 52,1 | -15,4 | -24,6 | -21,8 | |
| N = | 2 000 | kN | 41,2 | -9,6 | -21,7 | -19,0 | |
| N = | 2 250 | kN | 39,7 | -12,0 | -15,0 | -20,2 | |
| N = | 2 500 | kN | 45,7 | -6,2 | -15,7 | -21,3 | |
| N = | 2 750 | kN | 43,4 | -5,8 | -13,1 | -14,7 | |
| N = | 3 000 | kN | 42,9 | -7,9 | -16,0 | -13,4 | |
| N = | 3 250 | kN | 45,1 | -6,4 | -13,4 | -10,7 | |
| N = | 3 500 | kN | 39,0 | -11,9 | -18,2 | -19,5 | |
| N = | 3 750 | kN | 38,9 | -12,0 | -18,1 | -18,8 | |
| N = | 4 000 | kN | 43,8 | -9,0 | -14,9 | -18,9 | |
| N = | 4 250 | kN | 41,1 | -9,6 | -18,2 | -18,6 | |
| N = | 4 500 | kN | 42,5 | -2,5 | -16,1 | -13,5 | |
| N = | 4 750 | kN | x | -7,9 | -10,7 | -18,3 | |
| N = | 5 000 | kN | x | -4,3 | -10,5 | -11,2 | |
Diskrétní body zobrazené na obrázcích 9 až 12 odpovídají jednotlivým návrhovým situacím, které jsou definované konkrétními hodnotami meze kluzu oceli fy, návrhové tlakové síly NEd, a vzpěrné délky Lv-v. Z grafů je patrný značný rozptyl výsledků, který je zapříčiněný omezeným sortimentem rovnoramenných úhelníků. Aby bylo možné vysledovat trendy v závislostech mezi působící tlakovou sílou v nárožníku NEd (nebo požadovanou vzpěrnou únosností Nb,Rd), vzpěrnou délkou Lv-v a ekonomickou efektivitou použitého materiálu (vyjádřeno jako procentuální rozdíl cen vztažený k oceli S355J0), je potřeba konkrétní diskrétní hodnoty proložit vhodnou regresní křivkou. V provedené studii byla pro popis trendu zvolena logaritmická závislost ve formě:
y = A ln x + B (6)
kde:
x – odpovídá návrhové tlakové síle v nárožníku NEd (nebo požadované vzpěrné únosnosti Nb,Rd)
y – odpovídá procentuálnímu rozdílu ceny profilu (vztaženo k ceně oceli S355J0)
A, B – jsou konstanty určené regresní analýzou
Výsledné křivky jsou uvedeny na obrázcích 9 až 12.
S využitím odvozených regresních křivek je možné pro zvolený procentuální rozdíl cen (vztažený k oceli S355J0) určit závislost mezi vzpěrnou délkou Lv-v a tlakovou silou v nárožníku NEd. Výsledné „křivky uplatnění oceli“ určují meze ekonomicky efektivního použití posuzované jakosti oceli.
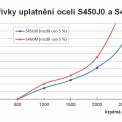
Na obrázku 13 jsou uvedeny křivky uplatnění pro oceli S450J0 a S460M, které byly spočteny pro hladinu rozdílu cen 5 % (tj. křivka popisuje návrhové situace, kdy se použitím výšepevné oceli ušetří 5 % za cenu materiálu v porovnání s ocelí S355J0). Oblast nad křivkou je oblastí efektivního uplatnění konkrétní jakosti oceli. Z křivek uvedených na obrázku 13 vyplývá, že při cenových hladinách uvedených v tabulkách 2 a 3 je ekonomicky výhodnější pro návrh tlačeného nárožníku použít rovnoramenné úhelníky z oceli S450J0.
Křivky uplatnění oceli mohou být použity jako praktický nástroj, který usnadní projektantům ocelových konstrukcí rozhodování o volbě ekonomicky výhodného konstrukčního materiálu. Křivky uplatnění oceli mohou využívat také obchodníci s hutním materiálem při optimalizaci cenové politiky.
ZÁVĚREČNÉ ZHODNOCENÍ
Článek se zaměřoval na specifika související s uplatněním rovnoramenných úhelníků z ocelí pevnostních tříd S450J0 a S460M v ocelových příhradových konstrukcích. Hlavní pozornost pak byla věnována návrhu a posudku spolehlivosti tlačených nárožníků příhradových stožárů [3, 4, 5].
Hlavním výstupem článku jsou zjištění ohledně ekonomické efektivity použití rovnoramenných úhelníků z výšepevných ocelí. Z výsledků provedené parametrické studie vyplývá, že při současném nastavení cen lze při použití rovnoramenných úhelníků z ocelí S450J0 či S460M dosáhnout maximálně 15% úspory v porovnání s nárožníky navrženými z tradiční oceli S355J0. Této úspory je dosaženo v případech, kdy tlačené prvky nejsou významně ovlivňovány účinky vzpěru. Se zvyšující se štíhlostí prvků klesá ekonomická efektivita použití výšepevných ocelí. Ekonomicky zajímavé 5% úspory vztažené k použití oceli S355J0 lze však dosáhnout u mnoha typických konstrukčních řešení příhradových stožárů v energetických přenosových soustavách.
Pro usnadnění rozhodování o vhodnosti použití příslušné jakostní třídy oceli při návrhu tlačených prutů z rovnoramenných úhelníků byly v programu Excel vytvořeny výpočetní pomůcky, které pro konkrétní návrhovou situaci umožní rychlé porovnání ekonomické výhodnosti jednotlivých typů ocelí. Rovněž byly vytvořeny křivky uplatnění ocelí S450J0 a S460M, pomocí kterých jsou při současném nastavení cen definovány návrhové situace (určené vzpěrnou délkou a návrhovou tlakovou silou v nárožníku) vedoucí k ekonomicky příznivému použití nárožníků z ocelí S450J0 a S460M. Křivky uplatnění mohou používat jak projektanti ocelových konstrukcí, tak také osoby odpovědné za cenovou politiku výrobce či prodejce hutního materiálu.
Materiál byl prezentován na konferenci Ocelové konstrukce 2014 v Karlově Studánce.
LITERATURA:
[1] CHEN, SF., Wang, XT. Buckling Strength of Single Angle Struts Part 1: Angles Subject to Axial Compression. Advances in structural engineering. Multi-Science Publ co Ltd., England, 2013, Volume 16, Issue 6, Pages 1129–1137. ISSN 1369-4332
[2] CHEN, SF., WANG, XT. Buckling Strength of Single Angle Struts Part 3: Cross-Bracing in Tower Structure. Advances in structural engineering. Multi-Science Publ co Ltd., England, 2013, Volume 16, Issue 6, Pages 1149–1160. ISSN 1369-4332
[3] BAN, HY., SHI, G., SHI, YJ., WANG, YQ. Column Buckling Tests of 420 MPa High Strength Steel Single Equal Angles. International journal of structural stability and dynamics. World Scientific Publ co Pte Ltd., Singapore, 2013, Volume 13, Issue 2, DOI: 10.1142/ S0219455412500691. ISSN 0219-4554
[4] LI, TJ., HAO, JP. Discussions on several parameters of Q460 high-strength single-angle equal-leg compression members. Advanced Materials Research. Trans Tech Publications Ltd., Switzerland, 2012, Volume 368–373, Pages 130–133, DOI: 10.4028/www.scientific.net/AMR.368-373.130. ISSN 1022-6680
[5] SHI, G et al. Tests and finite element analysis on the local buckling of 420 MPa steel equal angle columns under axial compression. Steel and composite structures. TECHNO-PRESS, South Korea, 2012, Volume 12, Issue 1, Pages 31–51. ISSN 1229-9367
[6] KŘIVÝ, V. et al. Použití rovnoramenných úhelníků z ocelí S450J0 a S460M v ocelových příhradových konstrukcích. In Modelování v mechanice 2014. Ostrava, VŠB-TU ostrava, 2014. ISBN 978-80-248-3320-0
Equal Angles from Steel Grades S450J0 and S460M in Lattice Steel Towers
The article deals with design and evaluation of pressed elements of steel lattice structures. An emphasis is placed mostly on design of lattice polescorners of steel lattice masts based on equal angle irons. The article evaluates implementation possibilities of the S450J0 and S460M quality class steels.