Finitní model styčníku tvořeného RHS a HEA profily

V praxi jsou pro různé typy staveb často navrhovány ocelové příhradové konstrukce z dutých průřezů nebo z kombinace dutých a otevřených průřezů. Použití takových konstrukcí má mnoho výhod (dvojose symetrický průřez, zkrácení vzpěrných délek, požadovaná únosnost při zachování subtilnosti konstrukce); na druhou stranu může být problematické navrhování jejich styčníků. Návrhové postupy, které udává Eurokód [1], jsou komplikované, obtížně kontrolovatelné a mají pouze omezené použití (geometrické podmínky, omezení materiálových charakteristik, pouze určité typy styčníků s danými způsoby zatížení).

Objevují se proto požadavky na ověření chování styčníků, které nevyhovují omezením daných Eurokódem a nelze je tedy přesně posuzovat na základě normových vztahů pro výpočet únosnosti styčníků. Pro tuto práci byl tedy vybrán příklad z praxe – zastřešení tvořené ocelovým příhradovým vazníkem s pásy z H‑profilů a s RHS mezipásovými pruty. V této konstrukci se vyskytuje styčník, který vybočuje z mezí, které udává Eurokód pro použití základních vzorců pro výpočet únosnosti takového styčníku. Konkrétně jde o úhel napojení tažené diagonály na spodní pás, který je menší než 30 °.

Cílem této práce je tedy ověřit, zda chování takového styčníku, který nezapadá do rozsahu použití normových vztahů, bude i přesto odpovídat tomu, které lze na základě normy očekávat.

ZPŮSOBY PORUŠENÍ STYČNÍKŮ DUTÝCH PRŮŘEZŮ DLE ČSN EN 1993-1-8
Výše uvedené norma [1] uvažuje u styčníků mezipásových prutů z CHS nebo RHS a pásů z průřezů I nebo H tyto způsoby porušení (obr. 1), viz také [2], nebo [3]:

• Porušení stojiny pásu zplastizováním, podrcením nebo ztrátou stability tvaru;
• Porušení pásu smykem;
• Porušení mezipásového prutu (trhliny ve svarech nebo mezipásových prutech)

Eurokód ve vzorcích pro výpočet únosnosti pro příslušné typy porušení nijak nezohledňuje síly nebo napětí, která vznikají v jednotlivých prutech. Vychází zde pouze z geometrie styčníku, z typů profilů a z hodnot mezí kluzu. Proto jsme se rozhodli porovnat chování styčníku, který je zatížen pouze silou v tažené diagonále a styčníku, který je zatížen reálnými silami (tedy jak silou v tažené diagonále, tak tahovou silou v dolním pásu).

ZÁKLADNÍ ÚDAJE O ŘEŠENÉM N STYČNÍKU
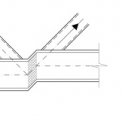
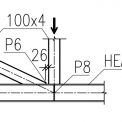
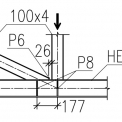
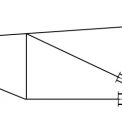
Styčník, který je předmětem řešení této práce, je tvořen spodním pásem z H‑profilu (konkrétně HEA 160) a mezipásovými pruty ze čtvercových dutých profilů (konkrétně RHS 100x4). Byly uvažovány dvě návrhové situace – nejdříve s výztuhou umístěnou jen pod tlačenou svislicí a poté s výztuhou také pod taženou diagonálou. Geometrie styčníku je znázorněna na obr. 2.

Pokud by byl daný styčník posouzen na základě vzorců uvedených v normě (přesto, že není splněna jedna z geometrických podmínek), bylo by pro něj v obou návrhových situacích rozhodující porušení mezipásového prutu. Pro druhou návrhovou situaci (tedy s výztuhou jak pod svislicí, tak pod diagonálou) by však únosnost byla téměř o 80 % vyšší (N_Rd,b ≈ 505 kN), než při umístění výztuhy jen pod svislici (N_Rd,a ≈ 281 kN).

NUMERICKÝ MODEL
Modely styčníku byly vytvořeny v MKP programu ANSYS 12.0 s využitím konečných prvků umožňující plastické chování materiálu i vliv velkých deformací. Pro modelování HEA profilu byl použit 3D konečný prvek SOLID 65 – definován osmi uzly a izotropními materiálovými vlastnostmi. Pro RHS pruty potom skořepinový konečný prvek SHELL 43 – definován čtyřmi uzly, čtyřmi tloušťkami a ortotropními materiálovými vlastnostmi [4].

Konečným prvkům byly zadány následující materiálové vlastnosti (podobně jako [5]): Youngův modul pružnosti E = 210 GPa a Poissonův součinitel o = 0,3. Při výpočtu byly uvažovány fyzikální i geometrické nelinearity (plastický výpočet s uvážením velkých deformací). Pružnoplastické chování materiálu bylo vyjádřeno bilineárním pracovním diagramem (viz např. [6]) s mezí kluzu f_y = 355 MPa a 5% zpevněním (tedy s hodnotou modulu zpevnění E₂ = 10 GPa).

Síly, kterými byl styčník zatěžován, vycházely z výsledků získaných na jednoduchém prutovém modelu celého vazníku. Na základě dostupných informací v literatuře (např. [7], [8]) byly nejdříve zvoleny následující okrajové podmínky (obr. 3. (a)):

• na obou koncích dolního pásu bylo zabráněno posunům ve směrech osy x, y i z a mezipásovým prutům bylo zabráněno posunům v rovině i z roviny (tedy umožněný pouze posun v osách prutů). Při takto zavedených okrajových podmínkách však v modelu docházelo a takovému rozložení sil, které se neshodovalo s tím, které bylo očekáváno na základě prutového modelu. Bylo proto nutné najít okrajové podmínky, které by více vystihovaly skutečné chování detailu konstrukce. Nakonec byly zvoleny tyto [obr. 3. (b)]:
• na koncích dolního pásu bylo zabráněno pouze posunům ve směru os x a z (tedy pohybům v ose prutu a z jeho roviny), případně byla vazba na levém konci nahrazena zatížením tahovou silou. Vazba proti svislému posunutí (ve směru osy y) byla umístěna na svislý prut.

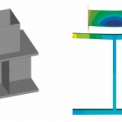
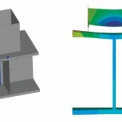
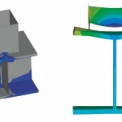
Jako další možný způsob řešení problému zavedení vhodných okrajových podmínek do modelu se nabízí možnost propojení 3D detailu konstrukce s prutovými prvky, pomocí kterých by se vymodelovala konstrukce jako celek (viz obr. 4). Okrajové podmínky a vnášené zatížení by se pak vztahovalo k celkové konstrukci a chování detailu by bylo odvozeno z chování celé soustavy. Správnost této hypotézy a vůbec realizovatelnost takového modelu je však třeba ještě prověřit.

VÝSLEDKY MODELOVÁNÍ
Rozpracovány byly celkem čtyři modely:

• styčník s výztuhou pouze pod tlačenou svislicí, zatížený jen tahovou sílou v diagonále
• styčník s výztuhou pouze pod tlačenou svislicí, zatížený tahovou sílou v diagonále a v dolním pásu
• styčník s výztuhou pod tlačenou svislicí i taženou diagonálou, zatížený jen tahovou sílou v diagonále
• styčník s výztuhou pouze pod tlačenou svislicí i taženou diagonálou, zatížený tahovou sílou v diagonále a v dolním pásu

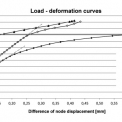
Kromě průběhů napětí byly na modelech sledovány také závislost svislé deformace (uy) středu pásnice (bod 2) na deformaci okraje pásnice (bod 1) HEA profilu (obr. 5., obr. 6.) a to ve dvou řezech – pod hranou připojené diagonály (řez A) a blízko jejího středu (tedy v blízkosti napojení druhé výztuhy – řez B) – viz obr. 7 – 9.

ZÁVĚR
Ze silově-deformačních křivek na obr. 5 a 6 lze vyvodit závěr, že únosnost styčníku s jednou výztuhou se bude pohybovat okolo 300 kN a styčník se dvěma výztuhami může být zatížen silou až 508 kN. Předpokládaným způsobem poruchy je porušení mezipásového prutu. U modelu se dvěma výztuhami však nebylo dosaženo takového porušení. Porucha, která u numerického modelu nastala, by se dala klasifikovat spíše jako porušení pásu smykem. Tento problém si vyžaduje ještě další, podrobnější modelování.

Podařilo se vytvořit numerický model, který vystihuje předpokládané chování styčníku. Jedním ze závěrů této práce je, že na samotnou únosnost styčníku nemá významný vliv, zda zatěžujeme pouze taženou diagonálu, nebo také spodní pás. Významný rozdíl je zde pouze ve výsledných hodnotách deformací, což je v souladu s principem výpočtu únosnosti takového styčníku dle EC3.

Dále výsledky získané sledováním deformací dvojice bodů pásnice HEA profilu naznačují, že ač styčník svou geometrií nespadá do mezí daných Eurokódem, jeho chování a únosnost se předpokladům této normy velice blíží.

Příspěvek byl realizován za finanční podpory projektu MŠMT – Studentská grantová soutěž VŠB – TUO.

LITERATURA:
[1] ČSN EN 1993-1-8, Eurokód 3: Navrhování ocelových konstrukcí – Část 1-8: Navrhování styčníků. Český normalizační institut, 2006. 126 s.
[2] Wald, F., Sokol, Z. Navrhování styčníků. Praha: Vydavatelství ČVUT, 1999. 144 pp. ISBN 80-01-02073-8
[3] Wardenier, J. Hollow Sections in Structural Applications. CIDECT, 2001. ISBN 0-471-49912-9
[4] Release 11.0 Documentation for ANSYS [online]. [cit. 2012-4-25]. Dostupné z http://www.kxcad.net/ansys/ANSYS/ansyshelp 
[5] JURČÍKOVÁ, A., ROSMANIT, M.: Numerické modelování svařovaného Tstyčníku. Sborník vědeckých prací Vysoké školy báňské – Technické univerzity Ostrava, řada stavební, Ostrava. Číslo 2, 2011. Ročník XI. ISSN 1213-1962, 6p.
[6] de Lima, L. R. O., Vellasco, P. C. G. da S., da Silva, J. G. S., Neves, L. F. da C., Bittencourt, M. C. A numerical analysis of tubular joints under static loading. In Proceedings of APCOM’07 in conjunction with EPMESC XI, Kyoto, Japan. December 3–6, 2007.
[7] Vegte, G. J. van der, Makino, Y., Wardenier, J. The influence of boundary conditions on the chord load effect for CHS gap K-joints. In Connections in Steel Structures. Amsterdam. June 3–4, 2004.
[8] Choo, Y. S., Qian, X. D., Wardenier, J. Effects of boundary conditions and chord stresses on static strength of thick-walled CHS joints. In Journal of Constructional Steel Research., Volume 62, Issue 4, April 2006, Pages 316–328.

A Finite Model of Joint Constituted by RHS and HEA Profiles
The subject of this text is modelling of a joint constituted by RHS (rectangular hollow section), web braces and an H‑profile bottom chord. Such a type of joint is based on a practical example, and its exceptional feature is a deviation from the geometric conditions given by Eurocode. The goal of this text is to fit the actual behaviour of this type of joint through the created model and subsequently to compare such behaviour with the one that can be expected on the basis of standardized relations.

Autoři

• Ing. Jurčíková Anežka
• Ing. Rosmanit Miroslav Ph.D.